文章目录
- 二次型与合同
- 二次型与标准型
- 二次型的分类
- 度量矩阵与合同
二次型与合同
二次型与标准型
Grant:二次型研究的是二次曲面在不同基下的坐标变换
由解析几何的知识,我们了解到二次函数的一次项和常数项只是对函数图像进行平移,并不会改变图形的形状和大小。以一元二次函数为例

而二次函数的二次项控制函数图像的大小和形状。以二元二次函数为例,观察 f ( x , y ) = 1 f(x,y)=1 f(x,y)=1 的截面图形

线性代数主要研究这些图形的二次项,通过线性变换使二次曲面变得规范简洁。
定义:
n
n
n 元二次齐次多项式
f
(
x
1
,
⋯
,
x
n
)
=
a
11
x
1
2
+
2
a
12
x
1
x
2
+
⋯
+
2
a
1
n
x
1
x
n
+
a
22
x
2
2
+
2
a
23
x
2
x
3
+
⋯
+
2
a
2
n
x
2
x
n
+
a
n
n
x
n
2
\begin{aligned} f(x_1,\cdots,x_n)=&a_{11}x_1^2+2a_{12}x_1x_2+\cdots+2a_{1n}x_1x_n \\ &+a_{22}x_2^2+2a_{23}x_2x_3+\cdots+2a_{2n}x_2x_n \\ &+a_{nn}x_n^2 \end{aligned}
f(x1,⋯,xn)=a11x12+2a12x1x2+⋯+2a1nx1xn+a22x22+2a23x2x3+⋯+2a2nx2xn+annxn2
称为二次型(quadratic form),这其实是二次曲面在一组坐标基下的解析表达式。
利用矩阵乘法,二次型可简记为
f
=
[
x
1
x
2
⋯
x
n
]
[
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋮
⋮
⋱
⋮
a
m
1
a
m
2
⋯
a
m
n
]
[
x
1
x
2
⋮
x
n
]
=
x
T
A
x
f=\begin{bmatrix}x_1&x_2&\cdots&x_n\end{bmatrix} \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n} \\ a_{21}&a_{22}&\cdots&a_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{m1}&a_{m2}&\cdots&a_{mn} \\ \end{bmatrix} \begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix} =\mathbf x^TA\mathbf x
f=[x1x2⋯xn]
a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn
x1x2⋮xn
=xTAx
其中
A
A
A 是对称阵,其主对角线元素是平方项的系数,其余元素
a
i
j
=
a
j
i
a_{ij}=a_{ji}
aij=aji 是二次项
x
i
x
j
x_ix_j
xixj 系数
2
a
i
j
2a_{ij}
2aij 的一半。显然,对称矩阵
A
A
A 与二次型
f
f
f 是相互唯一确定的。矩阵
A
A
A 及其秩分别称为二次型的矩阵和秩。
在某些情况下,没有交叉乘积项的二次型会更容易使用,即通过线性变换
x
=
C
y
\mathbf x=C\mathbf y
x=Cy 来消除交叉乘积项
f
=
x
T
A
x
=
x
=
C
y
y
T
(
C
T
A
C
)
y
=
y
T
Λ
y
f=\mathbf x^TA\mathbf x\xlongequal{\mathbf x=C\mathbf y}\mathbf y^T(C^TAC)\mathbf y=\mathbf y^T\Lambda\mathbf y
f=xTAxx=CyyT(CTAC)y=yTΛy
由于矩阵
A
A
A 是对称阵,由上节对称矩阵的对角化知道,总有正交矩阵
C
C
C,使
C
−
1
A
C
=
C
T
A
C
=
Λ
C^{-1}AC=C^TAC=\Lambda
C−1AC=CTAC=Λ
而
Λ
\Lambda
Λ 的对角线元素是
A
A
A 的特征值,于是二次型可简化为
f
=
λ
1
y
1
2
+
λ
2
y
2
2
+
⋯
+
λ
n
y
n
2
f=\lambda_1y_1^2+\lambda_2y_2^2+\cdots+\lambda_ny_n^2
f=λ1y12+λ2y22+⋯+λnyn2
这种只含平方项的二次型称为标准型(standard form)。显然,标准形的矩阵是对角阵。任何二次型都可通过正交变换化为标准型。系数全为 +1,-1或 0 的标准型叫做规范型(gauge form)。
定义:设
A
A
A和
B
B
B是
n
n
n阶矩阵,若有
n
n
n阶可逆矩阵
C
C
C,使
B
=
C
T
A
C
B=C^TAC
B=CTAC
则称矩阵
A
A
A和
B
B
B合同,记为
A
≃
B
A\simeq B
A≃B 。显然,合同矩阵即为二次型在不同基下的矩阵。
性质:设矩阵 A ≃ B A\simeq B A≃B
- 若 A A A 为对称阵,则 B B B 也为对称阵;
- 合同矩阵的秩相等 rank ( A ) = rank ( B ) \text{rank}(A)=\text{rank}(B) rank(A)=rank(B);
化二次型为标准型的三种方法:
- 求矩阵 A A A 的特征值和特征向量化为标准型;
- 使用多项式配方法化为标准型;
- 使用初等变换法将上方的矩阵
A
A
A 的位置变为对角阵(左乘为行变换,不影响下方单位阵变换)
[ A I ] → [ C T A C C ] \begin{bmatrix}A\\I\end{bmatrix}\xrightarrow{}\begin{bmatrix}C^TAC\\C\end{bmatrix} [AI][CTACC]
例:将椭圆方程 5 x 1 2 − 4 x 1 x 2 + 5 x 2 2 = 48 5x_1^2-4x_1x_2+5x_2^2=48 5x12−4x1x2+5x22=48 标准化
解:二次型的矩阵
A
=
[
5
−
2
−
2
5
]
A=\begin{bmatrix}5&-2\\-2&5\end{bmatrix}
A=[5−2−25] ,特征值分别为 3和 7,对应的单位特征向量为
u
1
=
[
1
/
2
1
/
2
]
,
u
2
=
[
−
1
/
2
1
/
2
]
\mathbf u_1=\begin{bmatrix}1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix}, \mathbf u_2=\begin{bmatrix}-1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix}
u1=[1/21/2],u2=[−1/21/2]
可使用特征向量
u
1
,
u
2
\mathbf u_1,\mathbf u_2
u1,u2 作为二次型的标准正交基。正交变换矩阵和标准型矩阵分别为
C
=
(
u
1
,
u
2
)
=
[
1
/
2
−
1
/
2
1
/
2
1
/
2
]
,
Λ
=
[
3
0
0
7
]
C=(\mathbf u_1,\mathbf u_2)=\begin{bmatrix}1/\sqrt{2}&-1/\sqrt{2}\\1/\sqrt{2}&1/\sqrt{2}\end{bmatrix},\quad \Lambda=\begin{bmatrix}3&0\\0&7\end{bmatrix}
C=(u1,u2)=[1/21/2−1/21/2],Λ=[3007]
C
C
C 可将
A
A
A 正交对角化,
Λ
=
C
T
A
C
\Lambda=C^TAC
Λ=CTAC 。所以正交变换
x
=
P
y
\mathbf x=P\mathbf y
x=Py 得到的标准型为
y
T
C
y
=
3
y
1
2
+
7
y
2
2
\mathbf y^TC\mathbf y=3y_1^2+7y_2^2
yTCy=3y12+7y22
新的坐标轴如图

二次型的分类
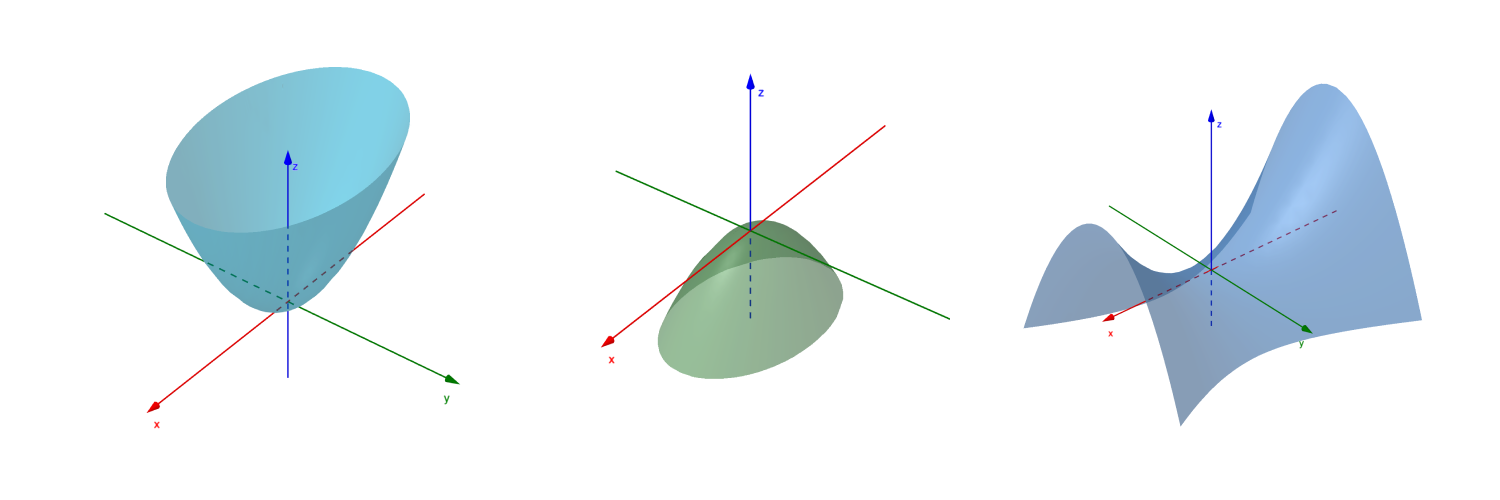
定义:设二次型 f = x T A x f=\mathbf x^TA\mathbf x f=xTAx ,如果对于任何 x ≠ 0 \mathbf x\neq 0 x=0
- 都有 f ( x ) > 0 f(\mathbf x)>0 f(x)>0,则称 f f f 为正定二次型,称 A A A 为正定矩阵;
- 都有 f ( x ) < 0 f(\mathbf x)<0 f(x)<0,则称 f f f 为负定二次型,称 A A A 为负定矩阵;
- 如果 f ( x ) f(\mathbf x) f(x) 既有正值又有负值,则称为不定二次型;
从上节可以看出二次型的标准型是不唯一的,但二次型的秩是唯一的,在化成标准型的过程中是不变的,即标准型中含有的非零平方项的个数是不变的。
惯性定理:二次型和标准型中系数为正的平方项的个数相同,称为正惯性指数;系数为负的平方项的个数也相同,称为负惯性指数;正负惯性指数之差称为符号差。
定理:
- n n n元二次型为正定的充要条件是它的正惯性指数为 n n n;
- 对称阵 A A A正定 ⟺ \iff ⟺ 特征值全为正 ⟺ \iff ⟺ 与单位阵合同 A ≃ I A\simeq I A≃I ;
- 对称阵 A A A 正定 ⟹ \implies ⟹ A − 1 A^{-1} A−1 正定;
度量矩阵与合同
Grant:合同矩阵为不同坐标系下的度量矩阵。
以二维空间为例,Grant 选用标准坐标系下的基向量
i
,
j
\mathbf i,\mathbf j
i,j,度量矩阵
A
=
[
⟨
i
,
i
⟩
⟨
i
,
j
⟩
⟨
j
,
i
⟩
⟨
j
,
j
⟩
]
A=\begin{bmatrix} \lang\mathbf i,\mathbf i\rang&\lang\mathbf i,\mathbf j\rang \\ \lang\mathbf j,\mathbf i\rang&\lang\mathbf j,\mathbf j\rang \end{bmatrix}
A=[⟨i,i⟩⟨j,i⟩⟨i,j⟩⟨j,j⟩]
而 Jennifer 使用另外一组基向量
i
′
,
j
′
\mathbf i',\mathbf j'
i′,j′,过渡矩阵
P
=
[
a
b
c
d
]
P=\begin{bmatrix} a&b \\ c&d \end{bmatrix}
P=[acbd]。即基向量
i
′
,
j
′
\mathbf i',\mathbf j'
i′,j′ 在 Grant 的坐标系下的坐标表示为
p
1
=
[
a
c
]
,
p
2
=
[
b
d
]
\mathbf p_1=\begin{bmatrix} a \\ c \end{bmatrix},\quad \mathbf p_2=\begin{bmatrix} b \\ d \end{bmatrix}
p1=[ac],p2=[bd]
因此, Jennifer 的基向量间的内积
⟨
i
′
,
i
′
⟩
=
p
1
T
A
p
1
⟨
i
′
,
j
′
⟩
=
p
1
T
A
p
2
⟨
j
′
,
i
′
⟩
=
p
2
T
A
p
1
⟨
j
′
,
j
′
⟩
=
p
2
T
A
p
2
\lang\mathbf i',\mathbf i'\rang=\mathbf p_1^TA\mathbf p_1\\ \lang\mathbf i',\mathbf j'\rang=\mathbf p_1^TA\mathbf p_2 \\ \lang\mathbf j',\mathbf i'\rang=\mathbf p_2^TA\mathbf p_1 \\ \lang\mathbf j',\mathbf j'\rang=\mathbf p_2^TA\mathbf p_2
⟨i′,i′⟩=p1TAp1⟨i′,j′⟩=p1TAp2⟨j′,i′⟩=p2TAp1⟨j′,j′⟩=p2TAp2
于是,Jennifer坐标系的度量矩阵
B
=
[
p
1
T
A
p
1
p
1
T
A
p
2
p
2
T
A
p
1
p
2
T
A
p
2
]
=
[
p
1
T
p
2
T
]
A
[
p
1
p
2
]
=
P
T
A
P
B=\begin{bmatrix} \mathbf p_1^TA\mathbf p_1&\mathbf p_1^TA\mathbf p_2 \\ \mathbf p_2^TA\mathbf p_1&\mathbf p_2^TA\mathbf p_2 \end{bmatrix}= \begin{bmatrix} \mathbf p_1^T \\ \mathbf p_2^T \end{bmatrix}A\begin{bmatrix} \mathbf p_1 & \mathbf p_2 \end{bmatrix} =P^TAP
B=[p1TAp1p2TAp1p1TAp2p2TAp2]=[p1Tp2T]A[p1p2]=PTAP
由此可知,合同矩阵刻画了两度量矩阵间的关系。
当然,也可通过两个向量的内积在不同的坐标系中的计算公式获得两个度量矩阵间的关系。由过渡矩阵知道,同一个向量从 Jennifer 的坐标到 Grant 的坐标变换公式为
y
=
P
x
\mathbf y=P\mathbf x
y=Px
在 Jennifer 的坐标系中,两向量
u
,
v
\mathbf u,\mathbf v
u,v 的坐标为
x
1
,
x
2
\mathbf x_1,\mathbf x_2
x1,x2 ,度量矩阵为
B
B
B 。内积计算公式
⟨
u
,
v
⟩
=
x
1
T
B
x
2
\lang\mathbf u,\mathbf v\rang=\mathbf x_1^TB\mathbf x_2
⟨u,v⟩=x1TBx2
在 Grant 的坐标系中,两向量
u
,
v
\mathbf u,\mathbf v
u,v 的的坐标为
y
1
,
y
2
\mathbf y_1,\mathbf y_2
y1,y2,度量矩阵为
A
A
A 。内积计算公式
⟨
u
,
v
⟩
=
y
1
T
A
y
2
=
(
P
x
1
)
T
A
(
P
x
2
)
=
x
1
T
(
P
T
A
P
)
x
2
\lang\mathbf u,\mathbf v\rang=\mathbf y_1^TA\mathbf y_2 =(P\mathbf x_1)^TA(P\mathbf x_2)=\mathbf x_1^T(P^TAP)\mathbf x_2
⟨u,v⟩=y1TAy2=(Px1)TA(Px2)=x1T(PTAP)x2
于是,我们得到了两坐标系中度量矩阵的关系
B
=
P
T
A
P
B=P^TAP
B=PTAP