1971. 寻找图中是否存在路径

目录

1、bfs - 邻接矩阵

 2、dfs - 邻接表

 3、并查集

---

1、bfs - 邻接矩阵

• 让源点source入队 取队头遍历未标记的邻接节点并入队
• 如果队伍里有dest目标节点 说明dest被遍历到 则return true

class Solution {
public:
    static const int N=2*1e5;
    bool st[N]={false};

    bool validPath(int n, vector<vector<int>>& edges, int source, int dest) 
    {
        vector<vector<int>> g(n);
        //vector<bool> st(n,false);
        for(vector<int>& x:edges)
        {
            int a=x[0],b=x[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        queue<int> q;
        q.push(source);
        st[source]=true;
        while(!q.empty())
        {
            int t=q.front();
            q.pop();
            if(t==dest) return true;
            for(int i=0;i<g[t].size();i++) 
                if(!st[g[t][i]])
                {
                    st[g[t][i]]=true;
                    q.push(g[t][i]);
                }
        }
        return false;
    }
};

 2、dfs - 邻接表

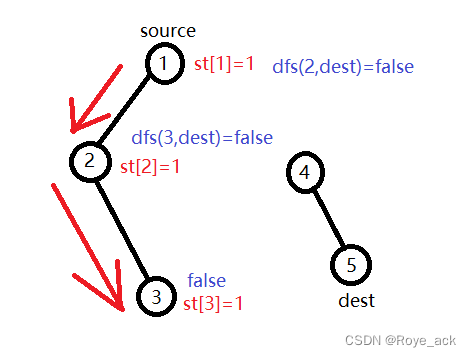
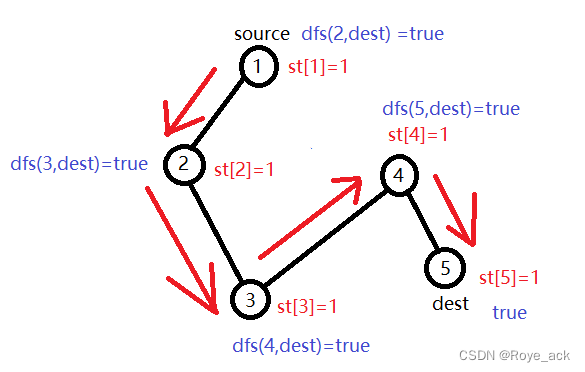
• 首先从顶点source 开始遍历并进行递归搜索
• 搜索时每次访问一个顶点next时，如果next==dest则该层返回true 不用继续遍历dest相邻的节点
• 否则将该顶点设为已访问，并递归访问与next相邻且未访问的顶点
• 如果搜到的最后一个点不能找到dest 则层层返回false
• 如果搜到一个点能找到dest 则层层返回true

class Solution {
public:
    static const int N=2*1e5+10;
    int h[N],e[N<<1],ne[N<<1],idx;
    bool st[N]={false};

    void add(int a,int b)
    {
        e[idx]=b,ne[idx]=h[a],h[a]=idx++;
    }

    bool dfs(int u,int dest)
    {
        st[u]=true;
        if(u==dest) return true;
        for(int i=h[u];~i;i=ne[i])
        {
            int t=e[i];
            if(!st[t]&&dfs(t,dest))
            {
                return true;
            }
        }
        return false;
    }

    bool validPath(int n, vector<vector<int>>& edges, int source, int dest) 
    {
        memset(h,-1,sizeof h);
        for(vector<int> &x:edges)
        {
            int a=x[0],b=x[1];
            add(a,b),add(b,a);
        }
        return dfs(source,dest);
    }
};

 3、并查集

find 查询a和b是否在一个集合内

unite 如果a和b不在一个集合 则f[a]=b 给a认个祖宗b 也就是把ab放一个集合内

class Solution {
public:
    static const int N=2*1e5+10;
    int f[N];

    int find(int x)
    {
        if(x!=f[x]) f[x]=find(f[x]);
        return f[x];
    }

    void unite(int x,int y)
    {
        int a=find(x),b=find(y);
        if(a!=b) f[a]=b;
    }

    bool validPath(int n, vector<vector<int>>& edges, int source, int dest) 
    {
        for(int i=1;i<=n;i++) f[i]=i;
        for(vector<int> &x:edges)
        {
            int a=x[0],b=x[1];
            unite(a,b);
        }
        return find(source)==find(dest);
    }
};