阈值回归模型是一类回归模型,其中预测变量与结果以阈值依赖的方式相关联。通过引入一个阈值参数(也称为转折点),阈值回归模型提供了一种简单而优雅、可解释的方法来建立结果和预测变量之间某些非线性关系的模型。在生物医学领域中,阈值回归模型有许多应用,如人类疫苗研究中免疫学检测数据分析,在这里感染风险和免疫反应生物标志物之间存在着依赖于阈值的关联。
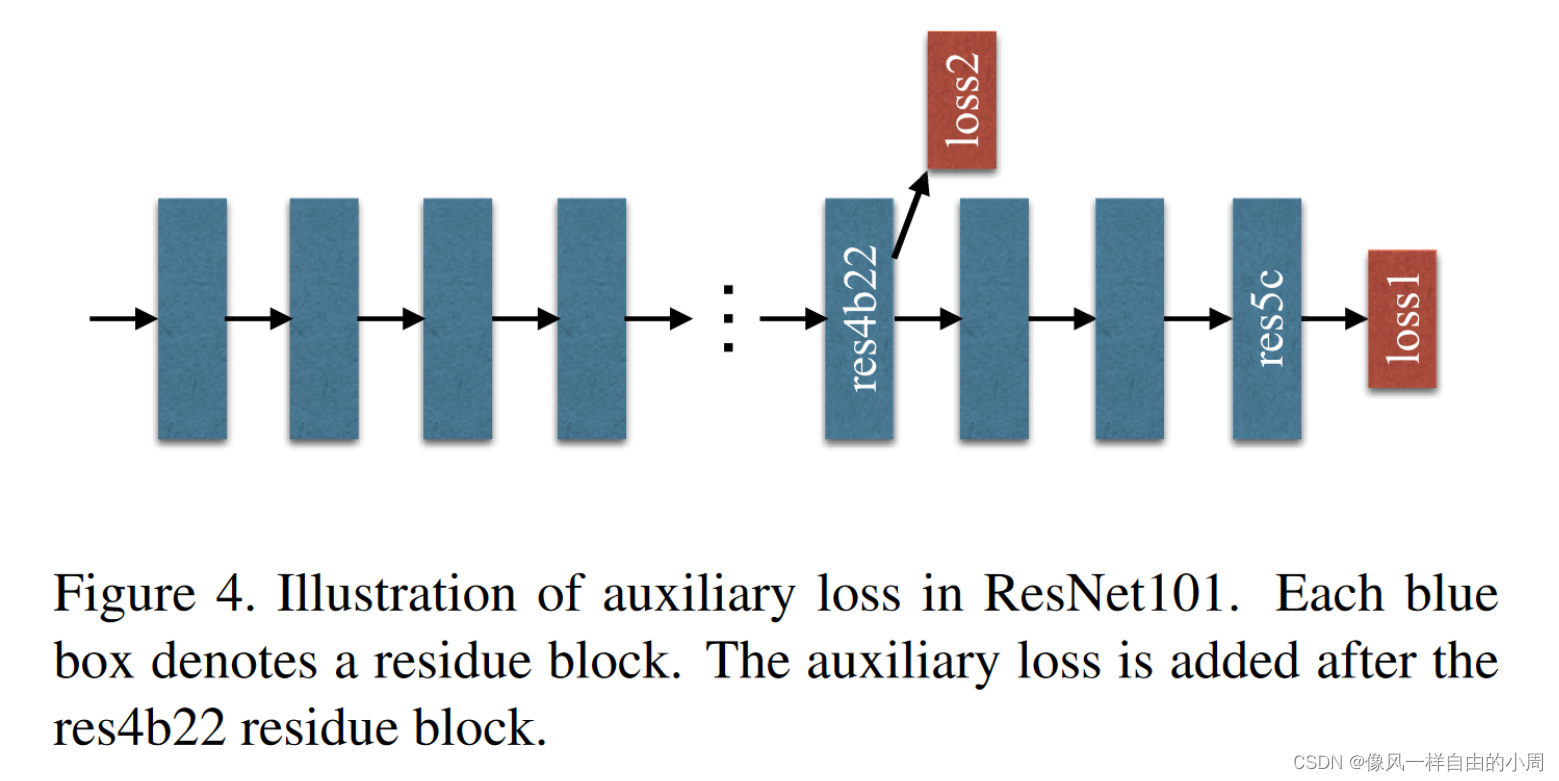
阈值回归模型可以采用许多形式,具体取决于在阈值处发生的情况。例如,下图展示了四种类型的阈值效应:步进(step)、铰链(hinge)、分段(segmented)和“stegmented”。步进和铰链模型是两种最基本的阈值效应形式,在阈值之前斜率为零。分段模型通过允许阈值之间的非零斜率来推广铰链模型;而分段模型,顾名思义,可以被视为步进和分段模型的融合。

四种阈值回归模型的方程如下:
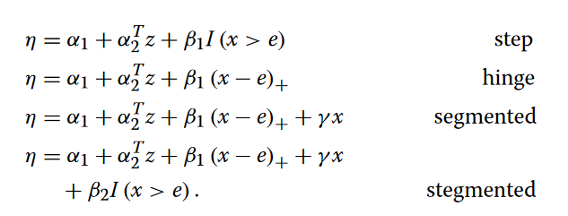
这里,e是阈值参数,x是具有阈值效应的预测变量,z表示额外的预测变量。当x > e时,I(x > e) = 1;否则为0。而(x - e)+表示铰链函数,在x > e时等于x - e,在其他情况下等于0。阈值回归模型与分段分析相关但不同,后者处理时间序列数据,并主要关注在自然轴线(如时间或染色体上的位置)上检测结构性变化。许多分段分析问题并非回归问题。在分段分析回归问题中,将时间序列数据按照转折点划分成区间;允许结果和所有预测因子之间的关系在各个区间内发生改变。换句话说,在改变点分析回归问题中同时对所有预测因子进行了阈值处理。另一方面,阈值回归模型基本上涉及建立非线性模型。从这个角度来看,阈值回归模型更类似于其他非线性回归方法(例如:拟合样条法)。
阈值模型和样条模型都能够建立结果和预测因子之间的非线性关系, 它们主要差异在于灵活性和易解释程度。例如,以铰链模型和具有两个自由度的自然三次样条为例。两者都有两个自由度;在铰链模型中,两个相关参数是β1和e。与铰链模型相比,样条模型更加灵活,但当这两种模型都能够提供合理的拟合时,铰链模型更容易解释。
虽然有许多软件程序可用于变点分析和回归样条模型,但适用于阈值回归模型的软件相对较少。目前最好的实现是R包segmented,它支持铰链和分段模型,并允许多个阈值。chngpt包通过提供三个独特贡献来补充segmented包:
(1) 它支持所有四种类型的阈值效应,并支持在受到阈值处理的预测因子和未经过阈值处理的预测因子之间进行交互项建模;
(2) segmented中使用了非平滑准则函数一级近似搜索方法,而chngpt提供两种替代搜索方法:精确法优化准则函数以获得全局最优解;平滑法利用基于逻辑函数平滑函数来近似准则函数。精确法保证找到全局最优解,但当样本量很大时可能会很慢;而像segmented一样快速但可能只能找到局部最优解;
(3) segmented不提供考虑阈值估计不确定性的置信区间,而chngpt可以提供这些信息。后者还包括model robust置信区间,即使数据生成模型并非真正的阈值模型,也旨在提供适当的覆盖率。
chngpt包的使用方法如下:
#安装chngpt包
install.packages(‘chngpt’)
library(‘chngpt’)
1. 线性回归模型
fit=chngptm(formula.1=Volume~1, formula.2=~Girth, family="gaussian", data=trees, type="segmented", var.type="bootstrap", weights=NULL)
formula.2 and formula.1: 阈值变量及模型的剩余参数
type: 阈值模型的类别
var.type: 使用bootsratp方式计算置信区间
weights: 可估计权重
est.method defaults to fastgrid and is recommended
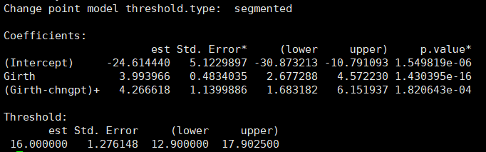
summary(fit)
plot(fit)
结果如Figure 1所示。
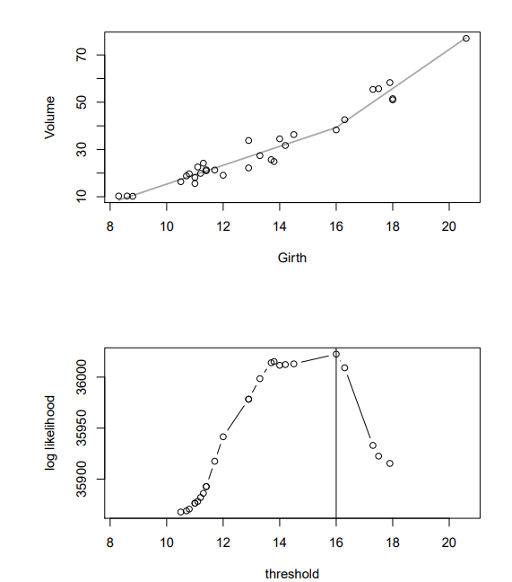
Figure 1: (top) 木材体积与周长的散点图。灰色的线表示虚线的分段模型。 (bottom) 子模型的对数似然与阈值参数的关系。
为验证是否有转折点,运行以下代码:
test=chngpt.test(formula.null=Volume~1, formula.chngpt=~Girth, trees, type="segmented", family="gaussian")
test

第一行给出进行的测试类型是默认的最大似然比测试,候选转折点为16。
2. Logistic回归模型
估计MTCT数据集中NAb_SF162L的铰链型变化点的逻辑回归模型。
library(splines)
fit=chngptm(formula.1=y~birth, formula.2=~NAb_SF162LS, family="binomial", dat.mtct, type="hinge", est.method="smoothapprox", var.type="robust", aux.fit=glm(y~birth + ns(NAb_SF162LS,3), dat.mtct, family="binomial"), weights=NULL)
formula.2 and formula.1:阈值变量和模型的其他部分
type:阈值模型的类型
est.method:推荐使用smoothapprox
var.type:建议采取稳健的置信区间
aux.fit:稳健方差估计所需的
weights:提供权重值
summary(fit)
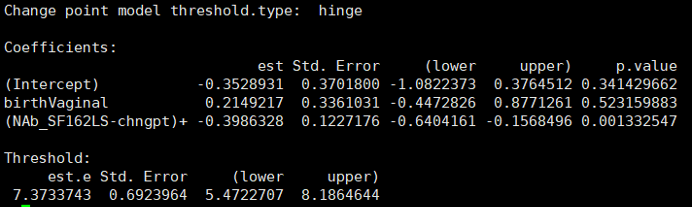
为了验证是否有change point,运行以下函数:
test=chngpt.test(formula.null=y~birth, formula.chngpt=~NAb_SF162LS, dat.mtct, type="hinge", family="binomial", main.method="score")
test
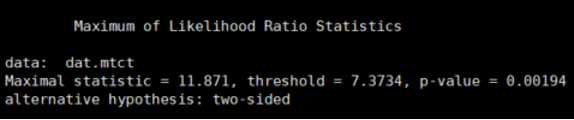
第一行给出进行的测试类型是默认的最大似然比测试,候选转折点为7.3734。
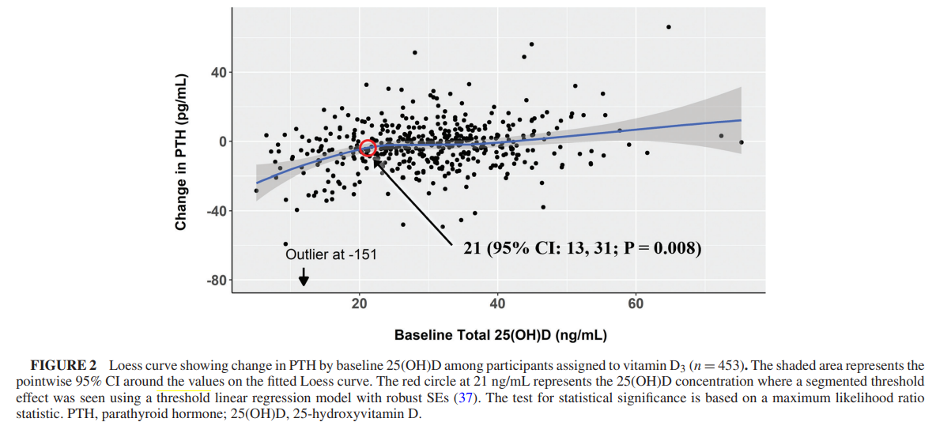
该方法被多项研究使用,如一项探索维生素D补充后的临床和生物标志特征的研究中(Clinical and biomarker modifiers of vitamin D treatment response: the Multi-Ethnic Study of Atherosclerosis),使用阈值回归模型发现,在25(OH)D浓度为21 ng/mL(95%CI:13,31)时,其与PTH的变化有分段阈值效应。
在四种类型的阈值模型中进行选择是一个复杂的问题。我们可以把这个问题分为两部分:(i) 阈值处是否发生跳跃;(ii) 斜率参数空间是否应该受到限制。第一个问题特别具有挑战性。对于某些过程,例如染色体上重组事件的发生,自然会出现跳跃。对于其他许多过程,真正的基本过程可能不是不连续的;尽管如此,不连续的阈值模型可以是对预测值的小范围内响应的突然转变的有用近似。使用何种模型的决定应该是基于统计学证据和科学考虑的结合。该种方法为非线性关联中阈值的寻找提供了一种切实可行的方案。
参考文献:
1. Fong Y, Huang Y, Gilbert PB, Permar SR. chngpt: threshold regression model estimation and inference. BMC Bioinformatics. 2017 Oct 16;18(1):454. doi: 10.1186/s12859-017-1863-x
2. Hsu S, Prince DK, Williams K, Allen NB, Burke GL, Hoofnagle AN, Li X, Liu KJ, McClelland RL, Michos ED, Psaty BM, Shea SJ, Rice KM, Rotter JI, Siscovick D, Tracy RP, Watson KE, Kestenbaum BR, de Boer IH. Clinical and biomarker modifiers of vitamin D treatment response: the Multi-Ethnic Study of Atherosclerosis. Am J Clin Nutr. 2022 Mar 4;115(3):914-924. doi: 10.1093/ajcn/nqab390
搜索公众号“单细胞学会”,获取更多信息。