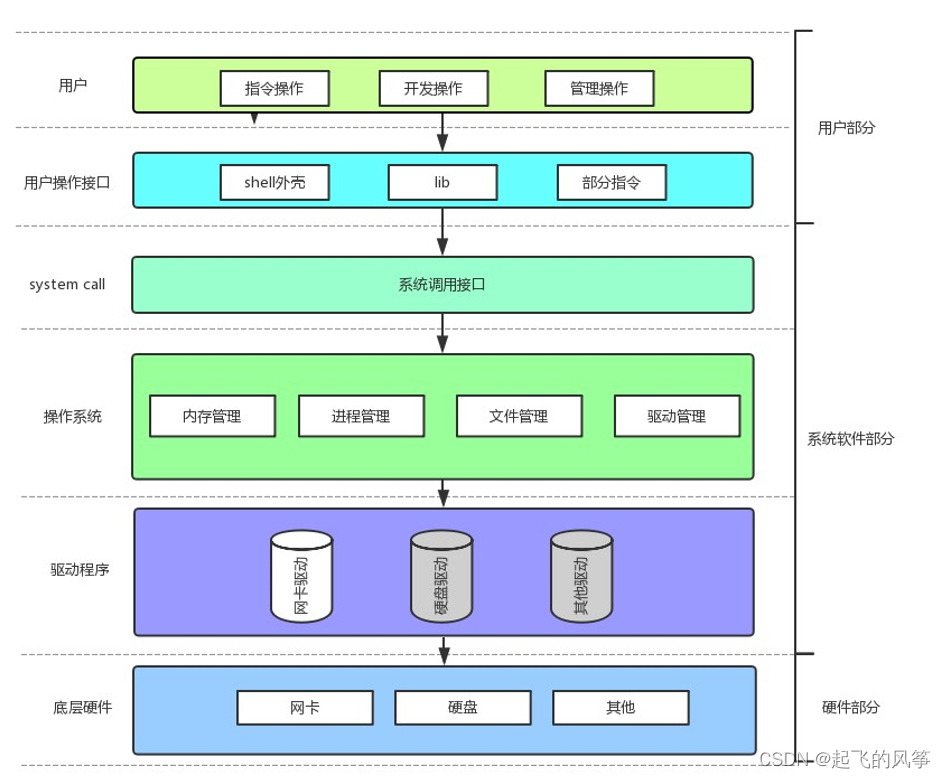
1、简介

ARIMA模型(Autoregressive Integrated Moving Average model)，差分整合移动平均自回归模型，又称整合移动平均自回归模型，时间序列预测分析方法之一。ARIMA(p,d,q)中，AR是"自回归"，p为自回归项数;MA为"滑动平均"，q为滑动平均项数，d为使之成为平稳序列所做的差分次数(阶数)。"差分"一词虽未出现在ARIMA的英文名称中，却是关键步骤。

2、模型原理

在描述ARIMA模型，那么就离不开AR、MA、ARMA模型，下面先阐述这两个模型。

2.1 AR模型(自回归)

自回归只适用于预测与自身前期相关的现象，数学模型表达式如下：

其中是当前值，是常数项，是阶数，是自相关系数，​​​​​是误差，同时

要符合正态分布。 

该模型反映了在t时刻的目标值值与前t-1~t-p个目标值之前存在着一个线性关系，即：

 2.2 MA模型（移动平均）

 移动平均模型关注的是自回归模型中的误差项的累加，数学模型表达式如下：

该模型反映了在t时刻的目标值值与前t-1~p个误差值之前存在着一个线性关系，即：

2.3 ARMA模型（自回归移动平均）

该模型描述的是自回归与移动平均的结合，具体数学模型如下：

2.4 ARIMA模型

基本原理：将数据通过差分转化为平稳数据，再将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。

AR是自回归，p为自回归项；MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数，一般做一阶差分，很少做二阶差分。

2.5 ACF

​​​ACF 是一个完整的自相关函数，可为我们提供具有滞后值的任何序列的自相关值。简单来说，它描述了该序列的当前值与其过去的值之间的相关程度。时间序列可以包含趋势，季节性，周期性和残差等成分。ACF在寻找相关性时会考虑所有这些成分

2.6 PACF
偏自相关函数PACF 只描述观测值和其滞后项之间的直接关系，调整了其他较短滞后项的影响。

2.7 拖尾与截尾

截尾：在大于某个常数k后快速趋于0为k阶截尾

拖尾：始终有非零取值，不会在k大于某个常数后就恒等于零(或在0附近随机波动)

例子：

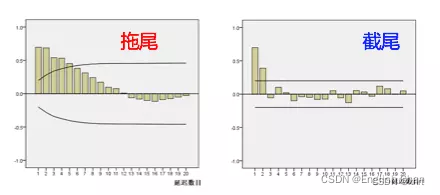
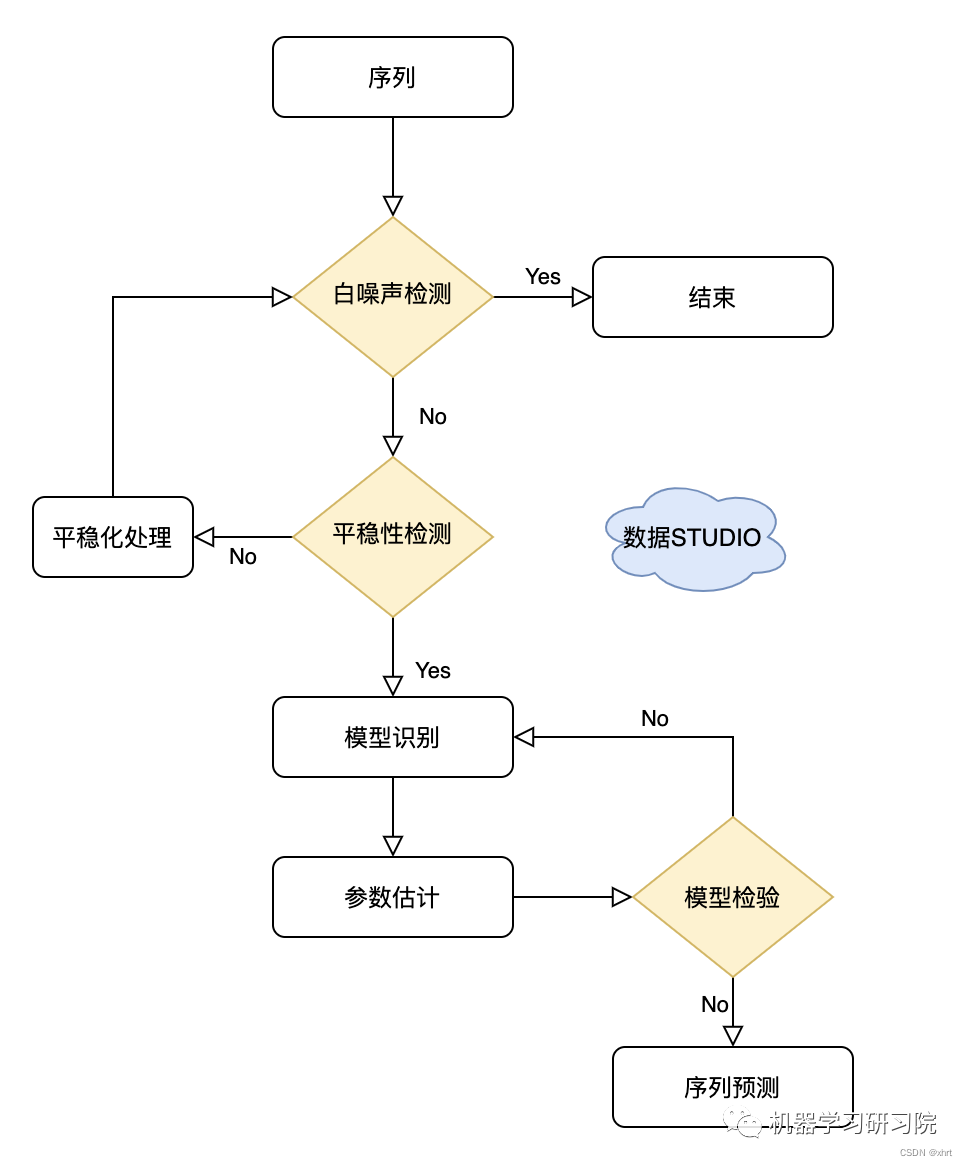
2.8 ARIMA模型运用流程

- （平稳性检验）根据时间序列的散点图、自相关系数和偏自相关系数、单位根检验(ADF)，来判断数据的平稳性；

- （平稳化处理）如果不平稳，则对其进行差分运算直到差分后的数据平稳，得到差分阶数d；

- （白噪声检测）在数据平稳后则对其进行白噪声检验，白噪声是指零均值常方差的随机平稳序列；

- （模型识别和定阶)如果是平稳非白噪声序列就计算ACF（自相关系数）、PACF（偏自相关系数），进行ARMA等模型识别。平稳化处理后，若偏自相关函数是截尾的，而自相关函数是拖尾的，则建立AR模型；若偏自相关函数是拖尾的，而自相关函数是截尾的，则建立MA模型；若偏自相关函数和自相关函数均是拖尾的，则序列适合ARIMA模型。可以采用BIC准则对模型进行定阶，确定p,q参数，从而选择最优模型；

- （模型检验）检验已确定的模型其残差序列是否为白噪声，如果不是白噪声，说明残差中还存在有用的信息，需要修改模型或者进一步提取；

-（模型预测）对已识别好的模型，确定模型参数，最后应用预测并进行误差分析。

3.定阶（p,d,q)

3.1 定d

因为AR（自回归）建立必须具有平稳性，所以在建立ARIMA模型也需要平稳性，使数据平稳性的方法可以讲数据进行差分处理，如一阶差分即t与t-1的差值，二阶差分为一阶差分基础上再进行一次差分，使数据平稳后的差分次数即为我们要定的参数d。

3.2 方法① 定p，q

• 若PACF偏自相关函数在p阶段后截尾，则截尾的阶数即为模型所确定的参数p。
• 若ACF自相关函数q阶段后截尾，则截尾的阶数即为模型所确定的参数q。

3.3 方法② 定p，q

采用AIC或BIC原则，模型中AIC或BIC值越小，模型就越好。

4.假设检验

下面介绍在用python实现ARIMA模型使用到的假设检验。

4.1单位根检验（ADF）

若单位根检验p值小于0.05则认为是平稳的。

4.2残差正态性检验

4.3残差序列独立性检验

参考链接：

ARIMA（p,d,q）模型原理及其实现 --------python_arima python_English Chan的博客-CSDN博客

理论加实践，终于把时间序列预测ARIMA模型讲明白了_风度78的博客-CSDN博客