1. 什么是汉诺塔

汉诺塔代码的功能：计算盘子的移动次数，由数学公式知，汉诺塔的盘子移动次数与盘子数n存在这样的关系，移动数 = $2^{n} - 1$ （由递推得到），后面可以用这个公式来验证我们代码。

汉诺塔的规制：（1）有三根相邻的柱子，标号为A,B,C。（2）A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。（3）现在把所有盘子一个一个移动到柱子B上，并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。

2. 三座台柱的汉诺塔

2.1 思路

总结：我们想知道n个盘子的次数，记住了，在求解f(n)的时候，我们直接默认f(n - 1)已经完了就可以了！这个在前面已经解释过了，在此不再鳌述。我们将n-1个盘子当作一个整体：这就是类似于分治求解子问题的思想

那么当由3个盘子时，就有公式：f(3,x,y,z) = f(2,x,z,y),x->z,f(2,y,x,z)；当有4个盘子时，就有公式：f(4,x,y,z) = f(3,x,z,y),x->z,f(3,y,x,z).从而推出f(n,x,y,z) = f(n,x,z,y),x->z,f(n,y,x,z)!

综上所述：也就是说我们想移动n个盘子，就需要先移动n - 1个盘子；移动n - 1个盘子，就需要先移动n - 2个盘子 ………………；移动2个盘子，就必须先移动1个盘子；

（1）而移动1个盘子就是递归的终止条件

（2）而n个盘子变成n - 1个盘子就是递归的大问题变成小问题的方法

2.2 三座台柱的汉诺塔代码

下列代码展示了盘子在柱子上移动的顺序：

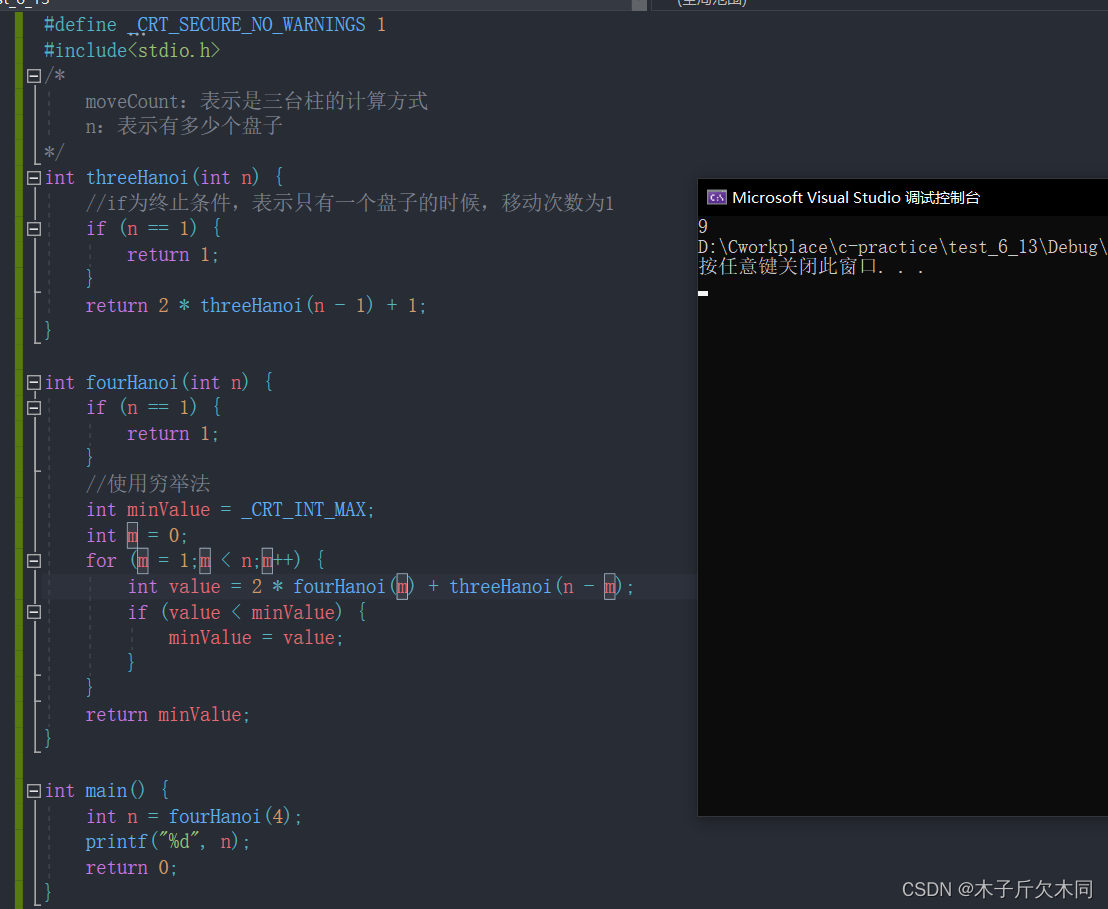
下列代码展示了有n个盘子，至少移动几次：

对（展示了有n个盘子，至少移动几次）解析：

ps：小伙伴们，图片将就着看吧哈哈哈，gif制作软件的免费用户是这样的w(ﾟДﾟ)w！

通过3个盘子，我们可以分析得：

（1）想先移动第3个盘子到最终位置，就必须先移动上面2个盘子；

（2）上面2个盘子总共移动了两趟，这就是2 * moveCount3(n - 1)的原因；

（3）最底下的盘子是移动了一次，这就是2 * moveCount3(n - 1) + 1的原因；

总结：

有n个盘子，上面n - 1个盘子需要移动两趟，而最底下，也就是第n个盘子是移动1次！！！

3. 四座台柱的汉诺塔

3.1 思路

算法思想:
用如下算法移动盘子(记为fourHanoi):
将A柱上n个盘子划分为上下两部分，上方部分共有m(1≤m≤n)个盘子，下方部分共有n - m个盘子。
步骤一：将A柱上面部分m个盘子使用fourHanoi算法经过C、D柱移至B柱。（此时C、D是中间柱）
步骤二：将A柱剩余的n - m个盘子使用threeHanoi算法经过C柱移至D柱。（此时C柱是中间柱）
步骤三：将B柱上的m个盘子使用fourHanoi算法经过A、C柱移至D柱。（此时A、C柱是中间柱）

这就有伙伴有疑问了，为什么不能全部都使用fourHanoi算法？

答：因为当fourHanoi算法将盘子转移到一定程度后，有个柱子上的盘子就不能动了，可以当作少了座台柱，也就是只能用threeHanoi算法移动其它盘子了。所以我们在计算的时候，就是在找fourHanoi算法将盘子转移到一定程度的临界值，也就是找多少个盘子能使用fourHanoi算法（找m）

根据算法的思想，可知：

（1）最优子结构性质:
四柱汉诺塔问题的最优解是用最少的移动次数将A柱上的盘子全部移到D柱上。当盘子总数为i时，我们不妨设使用fourHanoi的最少移动次数为f(i)。相应的threeHanoi 算法移动次数为g(n - m)，由于g(n - m)=2g(n - m - 1)+1=2^(n - m) -1,当n - m确定时，g(n - m)也是不变的。
f(m)为最优解时，其子问题f(m - 1)也必为最优解。如果f(m - 1)不是最优解，那么存在f’(m - 1) < f(m - 1)。用f’(m - 1)替换f(m - 1)将产生一个比f(m)更优的解。这与f(m)为最优解是矛盾的。所以本问题具有最优子结构性质。
（2）递归地定义问题的最优解:

根据上述fourHanoi算法得到最少移动次数f(m):

①当n = 1时，有 $f(n) = 1$