目录
- 一、选择题
- 题型一 (插入排序)
- 1、直接插入排序
- 2、折半插入排序
- 3、希尔排序
- 题型二(交换排序)
- 1、冒泡排序
- 2、快速排序
- 题型三(选择排序)
- 1、简单选择排序
- ~2、堆排序
- ~题型四(归并排序)
一、选择题
题型一 (插入排序)
1、直接插入排序
1、对n个元素进行直接插入排序,需要进行()趟处理。
A、n
B、n+1
C、n-1
D、2n
解析:(C)
直接插入排序是将要排序的序列按照关键字的大小插入至已排好序的子序列中,一直进行直到整个序列有序,所以对n个元素进行直接插入排序,一共插入元素n-1次,需要进行n-1趟。
2、对5个不同的数据元素进行直接插入排序,则最多需要进行的比较次数为()。
A、8
B、10
C、15
D、25
解析:(B)
考虑最坏情况下为最多需要进行的比较次数,即序列元素呈逆序排列时最多,由于此时从前到后依次需要比较1次、2次、3次、……、n-1次,所以n(n-1)/2=(5×4)/2=10。
3、对n个元素进行直接插入排序,最好情况下的时间复杂度为(),最坏情况下的时间复杂度为()。
A、O(n),O(n2)
B、O(n2),O(n)
C、O(n),O(n)
D、O(n2),O(n2)
解析:(A)
最好情况下,即序列元素都有序,此时只需比较元素而不需移动元素,比较次数为n-1次,故最好时间复杂度为O(n);而最坏情况下,即序列元素呈逆序排列时,此时比较次数和移动次数都到达最大值,均为n(n-1)/2,故最坏时间复杂度为O(n2);考虑平均情况,总的比较次数和移动次数约为n2/4,故直接插入排序的时间复杂度为O(n2)。
4、对n个元素进行直接插入排序,其空间复杂度为()
A、O(n)
B、O(1)
C、O(n2)
D、O(log2n)
解析:(B)
直接插入排序代码如下:
/*直接插入排序(由小到大)*/
void InsertSort(int r[],int n) {
int i,j,temp;
for(i=1; i<n; ++i) {
temp=r[i]; //将要插入的元素暂存在temp中
for(j>=0,j=i-1;temp<r[j];--j)
r[j+1]=r[j]; //向后挪一位
r[j+1]=temp; //找到插入位置并插入
}
}
由于直接插入排序中只使用了辅助变量,故空间复杂度为O(1)。
5、若排序的元素序列呈基本有序的前提下,选用效率最高的排序算法是()。
A、简单选择排序
B、快速排序
C、直接插入排序
D、归并排序
解析:(C)
由于序列基本有序,应该选用平均复杂度最小的排序算法。直接/折半插入排序、简单选择排序、冒泡排序都是简单型的排序算法,平均时间复杂度均为O(n2),但最好情况下,直接插入排序和冒泡排序可以达到O(n),折半插入排序可以达到O(nlog2n);堆排序、快速排序、归并排序都是改进型的排序算法,所以其时间复杂度均为O(nlog2n),在最好情况下可以达到O(nlog2n)。
2、折半插入排序
1、对n个元素进行折半插入排序,最好情况下的时间复杂度为(),最坏情况下的时间复杂度为()。
A、O(n2),O(nlog2n)
B、O(n),O(n2)
C、O(n2),O(n)
D、O(nlog2n),O(n2)
解析:(D)
折半插入排序与直接插入排序相比减少了比较元素的次数,其移动次数与直接插入排序是一样的。 先折半查找当前元素的插入位置,此时的时间复杂度为O(nlog2n),然后移动插入位置之后的所有元素,此时的时间复杂度为O(n2),故最好时间复杂度为O(nlog2n);而最坏情况下,故最坏时间复杂度为O(n2);考虑平均情况下,折半插入排序的时间复杂度仍为O(n2)。
2、对n个元素进行折半插入排序,其空间复杂度为()
A、O(n)
B、O(1)
C、O(n2)
D、O(log2n)
解析:(B)
折半插入排序代码如下:
/*折半插入排序*/
void Binary_InsertSort(int r[],int n) {
int i,j,temp,low,high,mid;
for(i=1; i<=n; i++) {
temp=r[i]; //将要插入的元素暂存在temp中
low=0;
high=i-1; //low和high为折半查找的范围
while(low<=high) {
mid=(low+high)/2; //mid取中间点
if(r[mid]>temp) //查找左半子表
high=mid-1;
else //查找右半子表
low=mid+1;
}
for(j=i-1; j>=high+1; j--) //先后移动元素,空出位置留给插入元素
r[j+1]=r[j];
r[j+1]=temp; //找到插入位置并插入
}
}
由于折半插入排序中只使用了辅助变量,故空间复杂度与直接插入排序相同,也为O(1)。
3、希尔排序
1、对初始数据序列(8, 3, 9, 11, 2, 1, 4, 7, 5, 10, 6)进行希尔排序。若第一趟排序结果为(1, 3, 7, 5, 2, 6, 4, 9, 11, 10, 8),第二趟排序结果为(1, 2, 6, 4, 3, 7, 5, 8, 11, 10, 9),则两趟排序采用的增 量(间隔)依次是()。
A、3,1
B、3,2
C、5,2
D、5,3
解析:(D)
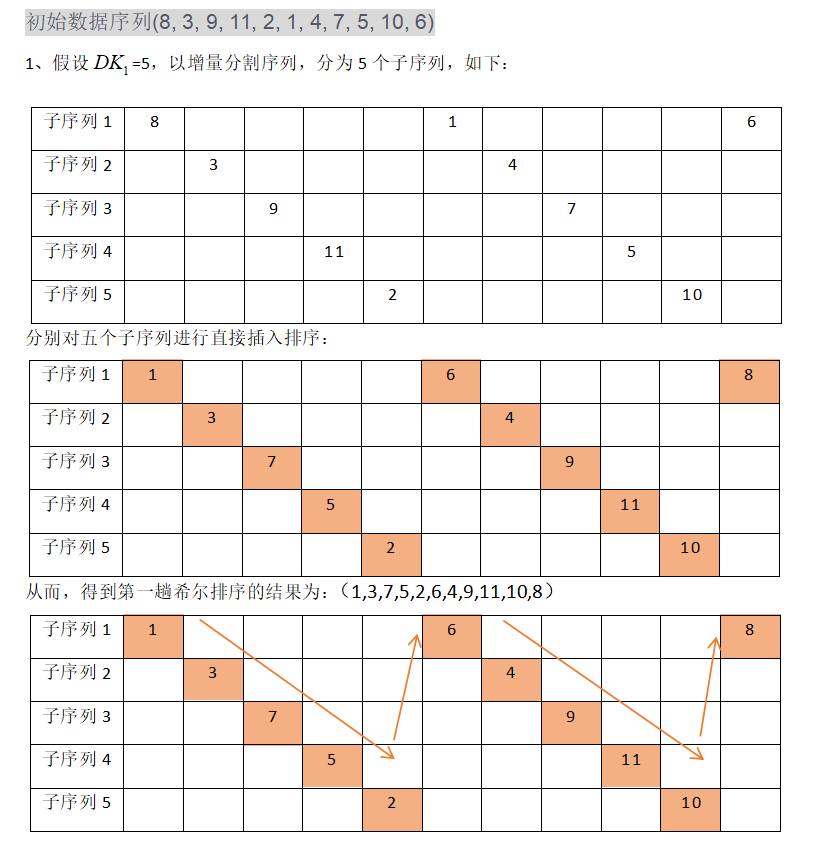

故两趟排序采用的增量依次为5和3。
2、希尔排序的组内排序采用的是()。
A、直接插入排序
B、折半插入排序
C、快速排序
D、归并排序
解析:(A)
希尔排序也称为缩小增量排序,它是通过选取一定的增量来排序的,其本质还是插入排序,通过增量将序列分为几个子序列,然后对每个子序列进行直接插入排序,当所有序列呈基本有序时,再进行一次直接插入排序即完成。
3、以下排序中,不稳定的排序算法是()。
A、冒泡排序
B、直接插入排序
C、希尔排序
D、归并排序
解析:(C)
由于分为不同子序列后,可能会出现改变其相对位置情况,所以希尔排序是不稳定的。
题型二(交换排序)
1、冒泡排序
1、对n个元素进行冒泡排序,最好情况下的时间复杂度为(),最坏情况下的时间复杂度为()
A、O(n2),O(n)
B、O(n),O(n2)
C、O(n),O(n)
D、O(n2),O(n2)
解析:(B)
最好情况下,即待排序结果恰好是排序后的结果,此时比较次数为n-1,移动次数和交换次数都为0,故最好时间复杂度为O(n);而最坏情况下,即排好的序列刚好与初始序列相反,呈逆序排列,则此时需要进行n-1趟排序,第i趟排序中要进行n-i次比较,即比较次数=交换次数=n(n-1)/2,由于每次交换都会移动3次元素从而来交换元素,即移动次数为3n(n-1)/2,故最坏时间复杂度为O(n2),而考虑平均情况下,故冒泡排序的时间复杂度为O(n2);
2、若用冒泡排序算法对序列{10、14、26、29、41、52}从大到小排序,则需要进行()次比较。
A、3
B、10
C、15
D、25
解析:(C)
元素52冒泡到最前面,比较5次;元素41冒泡到最前面,比较4次,……,所以一共比较次数为5+4+3+2+1=15次。
3、若用冒泡排序算法对序列{5,2,6,3,8}升序排序,且以从后向前进行比较,则第一趟冒泡排序的结果为()。
A、{2,5,3,6,8}
B、{2,5,6,3,8}
C、{2,3,5,6,8}
D、{2,3,6,5,8}
解析:(A)
首先,8>3,符合升序,不交换;
3<6,不符合升序,交换,此时为{5,2,3,6,8};
2<3,符合升序,不交换;
5>2,不符合升序,交换,此时为{2,5,3,6,8};
故第一趟冒泡排序的结果为{2,5,3,6,8}。
4、(多选)以下算法中,每趟排序时都能确定一个元素的最终排序位置的算法有()。
A、直接插入排序
B、折半插入排序
C、希尔排序
D、冒泡排序
E、快速排序
F、简单选择排序
G、堆排序
解析:(D、F、G)
冒泡排序、简单选择排序、堆排序每趟都可以确定一个元素的最终排序位置(堆排序中每趟形成整体有序的子序列),而快速排序只是确定每趟排序中枢轴元素的最终位置。
2、快速排序
1、对n个元素进行快速排序,若每次划分得到的左右子区间中的元素个数相等或只差一个,则排序的时间复杂度为()。
A、O(1)
B、O(nlog2n)
C、O(n2)
D、O(n)
解析:(B)
快速排序是对冒泡排序的一种改进算法,它又称为分区交换排序,通过多次划分操作来实现排序思想。每一趟排序中选取一个关键字作为枢轴,枢轴将待排序的序列分为两个部分,比枢轴小的元素移到其前,比枢轴大的元素移到其后,这是一趟快速排序,然后分别对两个部分按照枢轴划分规则继续进行排序,直至每个区域只有一个元素为止,最后达到整个序列有序。
当每次划分很平均时,即最好时间复杂度为O(nlog2n);而当序列原本正序或逆序时,此时性能最差,由于每次选择的都是最靠边的元素,即最坏时间复杂度为O(n2);故快速排序的平均时间复杂度为O(nlog2n)。
2、快速排序算法在()情况下最不利发挥其长处。
A、要排序的数据量太大
B、要排序的数据中含有多个相同值
C、要排序的数据个数为奇数
D、要排序的数据已基本有序
解析:(D)
快速排序算法的时间复杂度与递归层数有关,为O(n×递归层数),即取决于递归深度,若每次划分越均匀,则递归深度越低;越不均匀,则递归深度越深。可知,当初始序列有序或逆序时,快速排序的性能最差,其每次选择的都是最靠序列两边的元素,所划分的区域有一边为空,所以初始序列越接近无序或基本上无序,此时算法效率越高;越接近有序或基本上有序,算法效率越低。
3、下列4种排序算法中,关键字平均比较次数最少的是()。
A、插入排序
B、选择排序
C、快速排序
D、归并排序
解析:(C)
快速排序的最好时间复杂度为O(nlog2n)与其在平均情况下的所需时间最接近,与最坏情况O(n2)相比较远,所以快速排序是所有内部排序算法中平均性能最优的排序算法,其平均比较次数最少。
4、对n个关键字进行快速排序,最大递归深度为(),最小递归深度为()。
A、n;1
B、n;log2n
C、log2n;1
D、log2n;nlog2n
解析:(B)
由于快速排序代码中的递归进行需要栈来辅助,所以其需要的空间较大,这一点与其他排序算法相较特殊。其空间复杂度与递归层数(栈的深度)有关,为O(递归层数)。
二叉树的最大/小高度:
若将n个要排序的元素组成一个二叉树,
这个二叉树的层数就是递归调用的层数(栈的深度),
由于在n个结点的二叉树中,其最小高度=⌊ log2n ⌋
(以2为底n的对数然后再向上取整,取比自己大的最小整数),
其最大高度=n。
所以,其情况与二叉树一样,最好情况下为最小高度,为⌊ log2n ⌋层,即最小递归深度;而最坏情况下为最大高度,为n层,即最大递归深度。
5、对n个元素的序列进行快速排序时,其空间复杂度为()。
A、O(n)
B、O(n2)
C、O(log2n)
D、O(1)
解析:(C)
最好情况下为最小高度,为⌊ log2n ⌋,即最小递归深度,此时最好空间复杂度为O(log2n);而最坏情况下为最大高度,即最大递归深度,为n层,此时最坏空间复杂度为O(n),故平均空间复杂度为O(log2n)。
6、设一组初始记录关键字序列{5,8,6,3,2},以第一个记录关键字5为基准进行一趟从大到小快速排序的结果为()。
A、{2,3,5,8,6}
B、{2,3,5,6,8}
C、{3,2,5,8,6}
D、{3,2,5,6,8}
解析:(B)
以第一个元素5为枢轴,原位置空出,i和j指向序列的头、尾元素,开始进行第一趟快速排序:
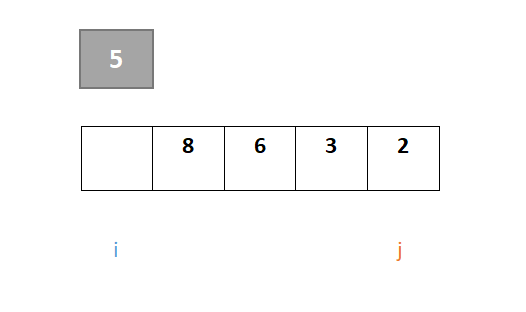
整个过程保证i指针左边是比枢轴元素小的元素,j指针右边是比枢轴元素大的元素(j指针找小于,i指针找大于)。首先对于j,从右往左一直寻找,找到小于枢轴元素的元素,若找到则j停下,由于元素2大于枢轴元素5,此时j的值与i的值交换:
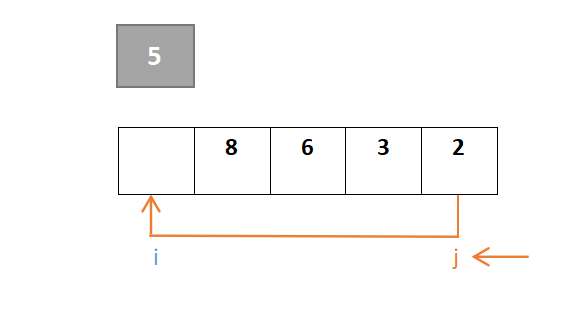
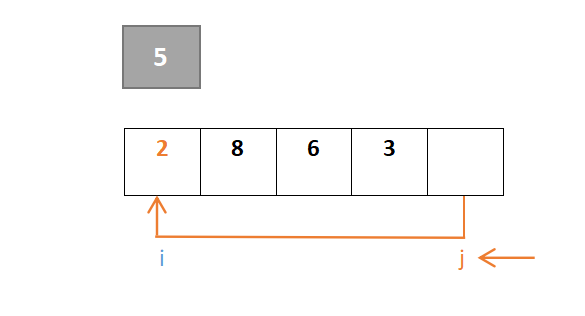
然后对于i,从左往右一直寻找,找到大于枢轴元素的元素,若找到则i停下,由于元素2小于则继续向右,到元素8停下,8>5:
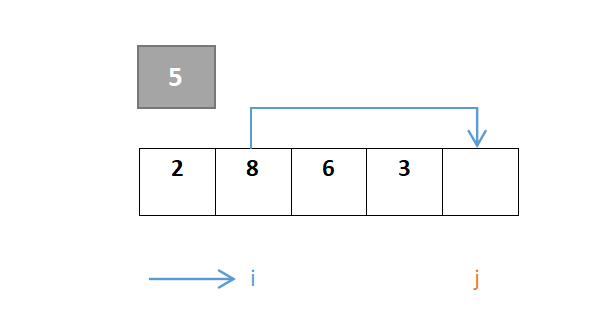
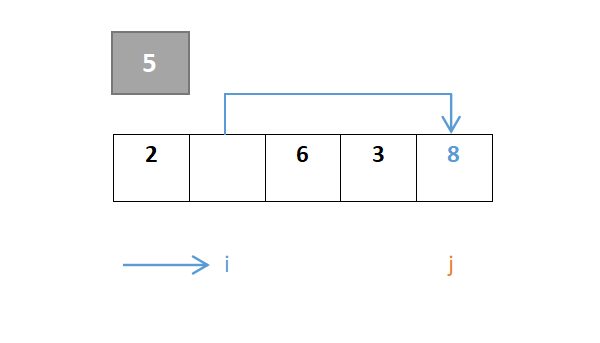
j继续移动,由于元素8大于则继续向左,到元素3停下,3<5,此时j与i交换:
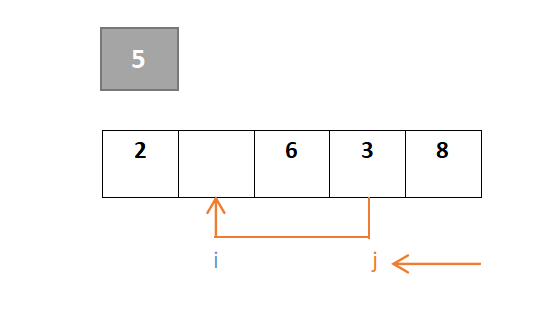
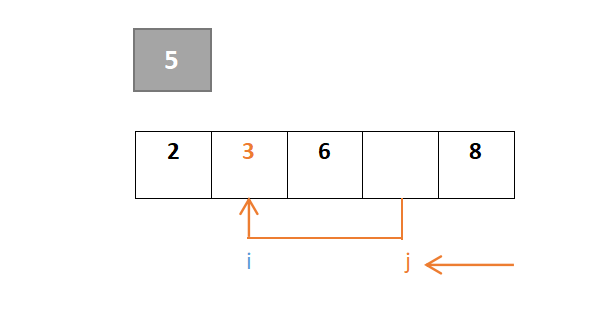
…………重复步骤:
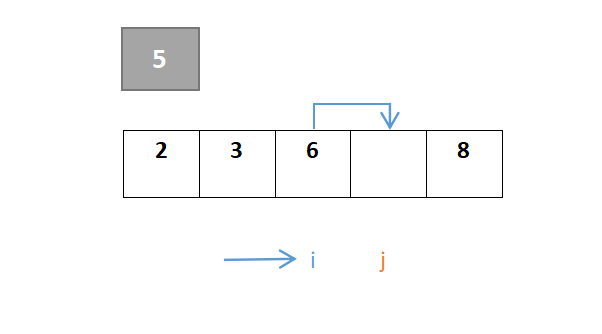
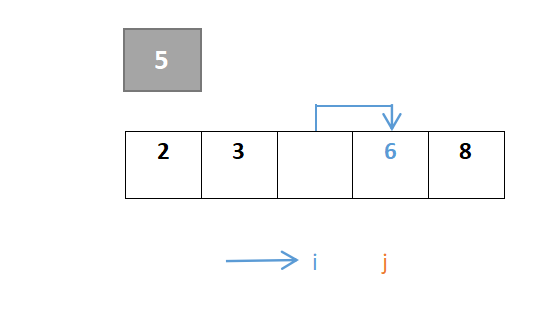
j继续移动,此时i与j相遇,最终位置即是枢轴元素的位置:
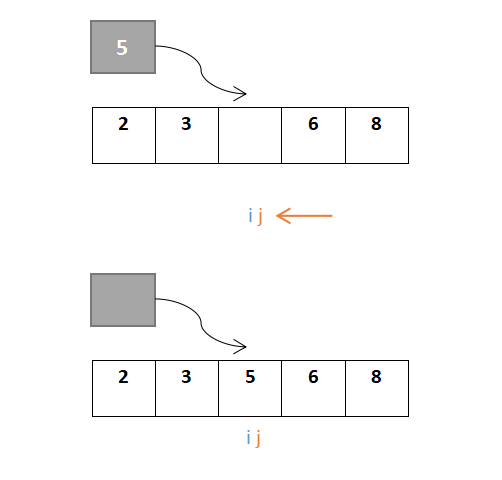
故快速排序的结果为{2,3,5,6,8}。
题型三(选择排序)
1、简单选择排序
1、下列4种排序方法中,排序过程中的比较次数与序列的初始状态无关的是()。
A、选择排序法
B、插入排序法
C、快速排序法
D、冒泡排序法
解析:(A)
选择排序的比较次数始终与初始序列无关。
2、对n个元素进行简单选择排序,时间复杂度为()。
A、O(n)
B、O(n2)
C、O(log2n)
D、O(nlog2n)
解析:(B)
在每一趟的简单选择排序过程中,每次从未排序的序列中选取当前元素最小的元素,将其作为有序子序列的第i,i+1,……个元素(加入到已排好序列的末尾),依次进行下去,即和第一个元素交换,依次进行交换,直到剩余一个元素,此时整个序列已经有序,每一趟简单选择排序可确定一个元素的最终位置。
所以相较于其他排序算法,其元素比较次数与初始序列无关,每次的比较次数分别是n-1,n-2,……,2,1,即n(n-1)/2=n2/2,故时间复杂度始终为O(n2)。
2、对n个元素进行简单选择排序,其比较次数和移动次数分别为()。
A、O(n),O(log2n)
B、O(log2n),O(n2)
C、O(n2),O(n)
D、O(nlog2n),O(n)
解析:(C)
简单选择排序的比较次数与初始序列无关,始终为O(n2),而移动次数与初始序列有关。当初始序列为正序时为最好情况,此时移动次数最少,即无需移动,移动次数为0次;而当序列逆序时为最坏情况,此时移动次数最多,为3(n-1)次,故平均移动次数为O(n)。
~2、堆排序
1、堆排序是一种()排序。
A、交换
B、选择
C、插入
D、归并
解析:(B)
2、下列4个序列中,哪一个是堆()。
A、70,40,60,25,10,20,15,5
B、70,60,40,5,25,20,15,10
C、70,60,25,10,20,40,15,5
D、70,40,60,5,20,25,15,10
解析:(A)
堆排序是利用堆树来进行排序,可以将其视为一棵完全二叉树,树中每一个结点均大于或等于其两个子结点的值,根结点是堆树中的最小值或最大值,即对应小根堆和大根堆,其定义如下表:
| 堆 | 条件 |
|---|---|
| 大根堆 | 完全二叉树中,根≥左,右 |
| 小根堆 | 完全二叉树中,根≤左,右 |
将题中的序列通过堆画出,序列中第一个元素为堆的根结点,均为元素70:
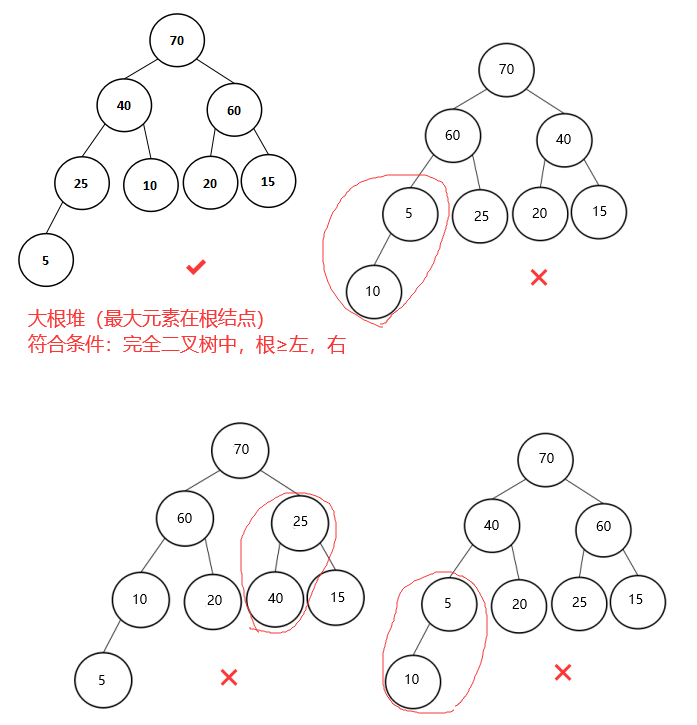
可知,其中B、C、D选项不符合大根堆的定义,且也不是小根堆,所以正确选项为A。
3、构建n个记录的初始堆,其时间复杂度为(),进行堆排序,其时间复杂度为()。
A、O(n),O(log2n)
B、O(n),O(nlog2n)
C、O(n2),O(log2n)
D、O(n2),O(nlog2n)
解析:(B)
初始建堆的时间复杂度为O(n),建堆过程中元素对比次数不超过4n,n-1趟交换和建堆过程中,根结点最多下坠h-1层,每下坠一层最多只需对比元素两次,每一趟不超过O(h)=O(log2n),即堆排序的时间复杂度为O(nlog2n),故堆排序的时间复杂度为O(n)+O(nlog2n)=O(nlog2n)。
4、向具有n个结点的堆中插入一个新元素的时间复杂度为(),删除一个元素的时间复杂度为()。
A、O(log2n),O(log2n)
B、O(nlog2n),O(nlog2n)
C、O(1),O(log2n)
D、O(n),O(nlog2n)
解析:(A)
对堆进行插入操作时,将要插入的结点放在堆的末尾,插入后,整个完全二叉树仍需满足堆的要求,对该结点进行向上调整,每次上升操作需对比元素1次,由于完全二叉树的高度为h=⌊log2n⌋+1,所以向n个结点的堆中插入一个新元素的时间复杂度为O(log2n)。
对堆进行删除操作时,删除的结点的位置就会空出来,此时需要将堆的末尾元素填到该位置,然后下调至合适位置,每次下调需对比元素1次或2次,删除操作也是取决于树的高度,即时间复杂度为O(log2n)。
6、对n个元素的序列进行堆排序时,所需要的附加存储空间是()。
A、O(n)
B、O(n2)
C、O(log2n)
D、O(1)
解析:(D)
在建立根堆后,将堆中堆顶元素与堆的最后一个元素进行交换,堆顶元素进入有序序列到达最终位置(从无序序列中被排出,符合选择排序的过程),然后对剩下的无序序列继续进行调整,依次进行下去,……,直到无序序列中剩余最后一个元素,此时整个序列已经有序,堆排序结束。堆排序的代码如下:
/*堆排序*/
void HeapSort(int r[],int n){
int i,temp;
for(i=n/2;i>=1;i--) //建立初始堆
Adjust(r,i,n);
for(i=n;i>1;i--){ //进行n-1次循环,完成堆排序
temp=r[1]; //将堆中最后一个元素与堆顶元素交换,将其放入最终位置
r[1]=r[i];
r[i]=temp;
Adjust(r,1,i-1); //对剩下的无序序列进行调整
}
}
由于只需要常数个辅助单元,所以空间复杂度为O(1)。
7、若只想的带1000个元素组成的序列中第10个最小元素之前的部分排序的序列,用()方法最快。
A、冒泡排序
B、快速排序
C、希尔排序
D、堆排序
解析:(D)
通常在一大堆数据中取k个最大/最小元素时,一般采用堆排序,由于其只需要调整10次大/小根堆,其时间与形成的树的高度成正比。
~题型四(归并排序)
1、下列排序算法中,占用辅助空间最多的是()。
A、快速排序
B、归并排序
C、堆排序
D、冒泡排序
解析:(B)
归并排序的代码如下:
/*归并*/
void Merge(int r[],int low,int mid,int high) {
int *r1=(int *)malloc((high-low+1)*sizeof(int)); //辅助数组r1
for(int k=low; k<=high; k++)
r1[k]=r[k]; //将r中的所有元素复制到r1中
for(i=low,j=mid+1,k=i; i<mid&&j<=high; k++) {//low指向为第一个有序表的第一个元素,j指向第二个有序表的第一个元素
if(r1[i]<=r1[j]) //比较r1的左右两段中的元素
r[k]=r1[i++]; //将较小值复制到r1中
else
r[k]=r[j++];
}
while(i<=mid)
r[k++]=r1[i++]; //若第一个表没有归并完的部分复制到尾部
while(i<=high)
r[k++]=r1[j++]; //若第二个表没有归并完的部分复制到尾部
}
/*归并排序*/
void MergeSort(int r[],int low,int high) {
if(low<high) {
int mid=(low+high)/2; //划分
MergeSort(r,low,mid); //对左有序子表递归
MergeSort(r,mid+1,high); //对右有序子表递归
Merge(r,low,mid,high); //归并
}
}
该算法中用到了递归工作栈,递归工作栈的空间复杂度为O(log2n),另外还需用到辅助数组,其空间复杂度为O(n),所以归并排序算法的空间复杂度为O(n)。而快速排序的平均空间复杂度为O(log2n),堆排序、冒泡排序的空间复杂度为均O(1)。