ACM模板二：树、图、并查集、DancingLink

news2024/11/27 17:52:07

目录

〇，全文说明、宏定义代码

一，二叉树

二，树状数组、线段树

三，多叉树

四，并查集、DancingLink、无向图、最小生成树

五，有向图、单源最短路径、连通分量、拓扑排序

六，网格图、回路链路、路径重建

七，test

〇，全文说明、宏定义代码

类里面和宏定义处都有接口注释，因为宏不体现具体参数，所以注释以类里面的为准。

所有代码放在一起是可以编译运行的，如果按照章来划分，最后一章是测试代码，其他任意一章都可以单独编译运行。

宏定义代码：

#define LOCAL //力扣不要本行代码，其他OJ随意

///（1）二叉树///
#define MaxDepth BinaryTree::maxDepth//求二叉树的深度，根节点深度是1
#define MinDepth BinaryTree::minDepth//叶子节点的最小深度
#define PreorderTraversal BinaryTree::preorderTraversal//二叉树的前序遍历
#define PostorderTraversal BinaryTree::postorderTraversal//二叉树的后序遍历
#define InorderTraversal BinaryTree::inorderTraversal//二叉树的中序遍历
#define BuildTree BinaryTree::buildTree//根据前序和中序重建二叉树，假设没有重复数字
#define BuildTree2 BinaryTree::buildTree2//根据中序和后序重建二叉树，假设没有重复数字
#define CountNodes BinaryTree::countNodes//求节点个数
#define CopyTree BinaryTree::copyTree//拷贝二叉树
#define IsSameTree BinaryTree::isSameTree//判断两棵二叉树是否全等
#define InvertTree BinaryTree::invertTree//左右翻转二叉树

///（2）树状数组、线段树///
// TreeArray 树状数组
// TreeArray2D 二维树状数组
// SegmentTree 线段树

///（3）多叉树///

///（4.1）并查集///
// Union 略。并查集

///（4.2）精确覆盖算法///
// DancingLink 略。精确覆盖算法

///（4.3）无向图///
#define UndirectedEdgeToFatherList UndirectedGraph::undirectedEdgeToFatherList//无向拓扑排序，输入无向无环图{{1，2}{1，3}{4，3}}的邻接表和指定根1，输出父节点表{4:3, 3:1, 2:1}
#define HasUndirectedCircle UndirectedGraph::hasCircle//根据无向图的邻接表判断是否有环
#define GetEdgeCover UndirectedGraph::getEdgeCover//给定一个2n个点的图，选出n条边，刚好覆盖这2n个点

///（4.4）最小生成树///
#define KruskalminCostTree Kruskal::minCostConnectPoints
#define PrimminCostTree Prim::minCostConnectPoints


///（5.1）有向图///
#define ReverseGraph DirectedGraph::reverseGraph//构建有向图的反向图
#define GetLongestPath DirectedGraph::getLongestPath//求有向无环图中的最长路径长度，出参nextNode是每个点的后继,len是每个点出发的最长路径长度
#define HasDirectedCircle DirectedGraph::hasCircle//根据有向图的邻接表判断是否有环
#define TopoSort DirectedGraph::topoSort//拓扑排序BFS版，输入n=3，g.edges={{0,1}{0,2}{1,2}}, 输出{0,1,2}，有环则输出为空

///（5.2）单源最短路径///
#define DijskraShortestPath Dijskra::shortestPath//求最短路,适用于不存在负权值的边的图
#define BellmanFordShortestPath BellmanFord::shortestPath//求最短路,适用于不存在负权值的环的图
#define SPFAShortestPath SPFA::shortestPath//求最短路,适用于不存在负权值的环的图

///（5.3）不区分有向图和无向图的通用操作///
#define GetSubGraph GraphOpt::getSubGraph//根据点集取子图

///（5.4）连通分量、拓扑排序///
#define SemiConnectComponent SemiConnect::semiConnectComponent//半连通分量分割
#define ConnectComponent KosarajuStrongConnect::connectComponent//Kosaraju算法，强连通分量分割
// TarjanUndirect 略。Tarjan算法，双连通分量分割
// TarjanStrongConnect 略。Tarjan算法，强连通分量分割
#define TopoSortNoCircle DirectedTopoSort::topoSortNoCircle //有向无环图拓扑排序，输入n=3，g.edges={{0,1}{0,2}{1,2}}, 输出{0,1,2}，有环则输出为空
#define TopoSort DirectedTopoSort::topoSort //有向图拓扑排序


///（6.1）网格图///
// GridGraph 略

///（6.2）回路或链路///
// Hierholzer 略。欧拉回路或链路
// Hamilton 略。哈密顿回路或链路

///（6.3）路径重建///
// ReBuild 略。路径重建

一，二叉树


#ifdef LOCAL
struct TreeNode {
	int val;
	TreeNode* left;
	TreeNode* right;
	TreeNode() : val(0), left(nullptr), right(nullptr) {}
	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
	TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
#endif
class BinaryTree
{
public:
	//求二叉树的深度，根节点深度是1
	static int maxDepth(TreeNode* root) {
		if (!root)return 0;
		return max(maxDepth(root->left), maxDepth(root->right)) + 1;
	}
	//叶子节点的最小深度
	static int minDepth(TreeNode* root) {
		if (!root)return 0;
		return min_depth(root);
	}
	//二叉树的前序遍历
	static vector<int> preorderTraversal(TreeNode* root) {
		vector<int>v1;
		if (root == NULL)return v1;
		v1.insert(v1.end(), root->val);
		vector<int>v2 = preorderTraversal(root->left);
		v1.insert(v1.end(), v2.begin(), v2.end());
		v2 = preorderTraversal(root->right);
		v1.insert(v1.end(), v2.begin(), v2.end());
		return v1;
	}
	//二叉树的后序遍历
	static vector<int> postorderTraversal(TreeNode* root) {
		vector<int>v1;
		if (root == NULL)return v1;
		vector<int>v2 = postorderTraversal(root->left);
		v1.insert(v1.end(), v2.begin(), v2.end());
		v2 = postorderTraversal(root->right);
		v1.insert(v1.end(), v2.begin(), v2.end());
		v1.insert(v1.end(), root->val);
		return v1;
	}
	//二叉树的中序遍历
	static vector<int> inorderTraversal(TreeNode* root) {
		vector<int>v1;
		if (root == NULL)return v1;
		v1 = inorderTraversal(root->left);
		v1.insert(v1.end(), root->val);
		vector<int>v2 = inorderTraversal(root->right);
		v1.insert(v1.end(), v2.begin(), v2.end());
		return v1;
	}
	//根据前序和中序重建二叉树，假设没有重复数字
	static TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
		return build_tree(preorder, 0, inorder, 0, inorder.size());
	}
	//根据中序和后序重建二叉树，假设没有重复数字
	static TreeNode* buildTree2(vector<int>& inorder, vector<int>& postorder) {
		return build_tree2(postorder, 0, inorder, 0, inorder.size());
	}
	//求节点个数
	static int countNodes(TreeNode* root) {
		if (!root)return 0;
		return countNodes(root->left) + countNodes(root->right) + 1;
	}
	//拷贝二叉树
	static TreeNode* copyTree(TreeNode* root)
	{
		if (!root)return root;
		return new TreeNode(root->val, copyTree(root->left), copyTree(root->right));
	}
	//判断两棵二叉树是否全等
	static bool isSameTree(TreeNode* r1, TreeNode* r2)
	{
		if (r1 == NULL && r2 == NULL)return true;
		if (r1 == NULL || r2 == NULL)return false;
		if (r1->val != r2->val)return false;
		return isSameTree(r1->left, r2->left) && isSameTree(r1->right, r2->right);
	}
	//左右翻转二叉树
	static TreeNode* invertTree(TreeNode* root) {
		if (!root)return root;
		TreeNode* p = root->left, *q = root->right;
		root->left = q, root->right = p;
		invertTree(p);
		invertTree(q);
		return root;
	}
private:
	static int min_depth(TreeNode* root) {
		if (!root)return 1234567890;
		if (!root->left && !root->right)return 1;
		return min(min_depth(root->left), min_depth(root->right)) + 1;
	}
	static TreeNode* build_tree(vector<int>& preorder, int s1, vector<int>& inorder, int s2, int len) {
		if (len <= 0)return NULL;
		TreeNode* ans = new TreeNode;
		ans->val = preorder[s1];
		auto loc = find(inorder.begin() + s2, inorder.begin() + s2 + len, preorder[s1]);
		ans->left = build_tree(preorder, s1 + 1, inorder, s2, loc - inorder.begin() - s2);
		ans->right = build_tree(preorder, loc - inorder.begin() - s2 + s1 + 1, inorder, loc - inorder.begin() + 1, len - (loc - inorder.begin() - s2) - 1);
		return ans;
	}
	static TreeNode* build_tree2(vector<int>& postorder, int s1, vector<int>& inorder, int s2, int len) {
		if (len <= 0)return NULL;
		TreeNode* ans = new TreeNode;
		ans->val = postorder[s1 + len - 1];
		auto loc = find(inorder.begin() + s2, inorder.begin() + s2 + len, postorder[s1 + len - 1]);
		ans->left = build_tree2(postorder, s1, inorder, s2, loc - inorder.begin() - s2);
		ans->right = build_tree2(postorder, loc - inorder.begin() - s2 + s1, inorder, loc - inorder.begin() + 1, len - (loc - inorder.begin() - s2) - 1);
		return ans;
	}
};

二，树状数组、线段树


template<int maxLen = 100000>
class TreeArray
{
public:
	TreeArray(int len)//len是元素实际数量,元素id范围是[1,n]
	{
		this->n = len;
		memset(c, 0, sizeof(int)*(len + 1));
	}
	void add(int i, int x)
	{
		while (i <= n)
		{
			c[i] += x;
			i += (i&(-i));
		}
	}
	int getSum(int i)
	{
		int s = 0;
		while (i)
		{
			s += c[i];
			i -= (i&(-i));
		}
		return s;
	}
private:
	int n;
	int c[maxLen+5];
};

template<int maxLen = 1000>
class TreeArray2D
{
public:
	TreeArray2D(int len)//len是元素实际数量,元素id范围是[1,n]*[1,n]
	{
		this->n = len;
		for (int i = 0; i <= n; i++)memset(c[i], 0, sizeof(int)*(n + 1));
	}
	void add(int x, int y, int a = 1)
	{
		for (int i = x; i <= n; i += (i&(-i)))
			for (int j = y; j <= n; j += (j&(-j)))c[i][j] += a;
	}
	int getSum(int x, int y)
	{
		int s = 0;
		for (int i = x; i > 0; i -= (i&(-i)))
			for (int j = y; j > 0; j -= (j&(-j)))
				s += c[i][j];
		return s;
	}
private:
	int n;
	int c[maxLen +5][maxLen +5];
};

//type=0,1,2,3,4分别表示sum型、min型、max型、minId型、maxId型线段树
//maxLen是元素最大数量
template<int type, int maxLen = 100000, typename T = int>
class SegmentTreeBase
{
public:
	T* getData()//先调getData更新数据再调build
	{
		return num;
	}
	void build(int len)//len是元素实际数量,元素id范围是[1,n]
	{
		this->n = len;
		build(1, 1, n);
	}
	void update(int uplace, T value)//1<=uplace<=n
	{
		num[uplace] = value;
		update(1, 1, n, uplace);
	}
	T query(int x, int y)//1<=x<=y<=n
	{
		return query(1, 1, n, x, y);
	}
protected:
	template<typename T2>
	inline T2 op(T2 a, T2 b)
	{
		if (type == 3)return num[a] < num[b] ? a : b;
		if (type == 4)return num[a] > num[b] ? a : b;
		if (type == 0)return a + b;
		return type == 1 ? min(a, b) : max(a, b);
	}
	void build(int key, int low, int high)
	{
		if (low == high)
		{
			ans[key] = type > 2 ? low : num[low];
			return;
		}
		int mid = (low + high) / 2;
		build(key * 2, low, mid);
		build(key * 2 + 1, mid + 1, high);
		ans[key] = op(ans[key * 2], ans[key * 2 + 1]);
	}
	void update(int key, int low, int high, int uplace)
	{
		if (low == high)
		{
			ans[key] = type > 2 ? low : num[low];
			return;
		}
		int mid = (low + high) / 2;
		if (uplace <= mid)update(key * 2, low, mid, uplace);
		else update(key * 2 + 1, mid + 1, high, uplace);
		ans[key] = op(ans[key * 2], ans[key * 2 + 1]);
	}
	T query(int key, int low, int high, int x, int y)
	{
		if (low == x && high == y)return ans[key];
		int mid = (low + high) / 2;
		if (mid < x)return query(key * 2 + 1, mid + 1, high, x, y);
		if (mid >= y)return query(key * 2, low, mid, x, y);
		T a = query(key * 2, low, mid, x, mid);
		T b = query(key * 2 + 1, mid + 1, high, mid + 1, y);
		return  op(a, b);
	}
protected:
	int n;
	T num[maxLen + 1];
	T ans[maxLen * 4 + 10];
};
//sum型线段树拓展，支持查询前缀和
template<int maxLen = 100000, typename T = int>
class SegmentTreeTypeSum :public SegmentTreeBase<0, maxLen, T>
{
	using BASE = SegmentTreeBase<0, maxLen, T>;
public:
	int queryPreSum(T x)
	{
		return queryPreSum(1, 1, BASE::n, x);
	}
private:
	int queryPreSum(int key, int low, int high, T x)
	{
		if (low == high)return low;
		int mid = (low + high) / 2;
		if (x <= BASE::ans[key * 2])return queryPreSum(key * 2, low, mid, x);
		return queryPreSum(key * 2 + 1, mid + 1, high, x - BASE::ans[key * 2]);
	}
};
//5种线段树拓展，支持区间更新，区间查询
template<int type, int maxLen = 100000, typename T = int, T invalid = -1>
class SegmentTree :public SegmentTreeBase<type, maxLen, T>
{
	using BASE = SegmentTreeBase<type, maxLen, T>;
public:
	void build(int len)//len是元素实际数量,元素id范围是[1,n]
	{
		BASE::n = len;
		build(1, 1, BASE::n);
	}
	void update(int uplace, T value)//1<=uplace<=n，覆盖父类函数
	{
		update(uplace, uplace, value);
	}
	void update(int x, int y, T value)//1<=x<=y<=n
	{
		update(1, 1, BASE::n, x, y, value);
	}
	T query(int x, int y)//1<=x<=y<=n
	{
		return query(1, 1, BASE::n, x, y);
	}
private:
	static inline T opMulti(T a, int num)
	{
		if (!type)return a * num;
		return a;
	}
	void build(int key, int low, int high)
	{
		if (low == high)
		{
			BASE::ans[key] = type > 2 ? low : BASE::num[low];
			lazy[key] = invalid;
			return;
		}
		int mid = (low + high) / 2;
		build(key * 2, low, mid);
		build(key * 2 + 1, mid + 1, high);
		BASE::ans[key] = BASE::op(BASE::ans[key * 2], BASE::ans[key * 2 + 1]);
		lazy[key] = invalid;
	}
	void update(int key, int low, int high, int x, int y, T value)
	{
		if (low == x && high == y)
		{
			BASE::ans[key] = type > 2 ? x : opMulti(value, high - low + 1);
			lazy[key] = value;
			if (x == y)BASE::num[x] = value;
			return;
		}
		if (lazy[key] != invalid)down(key, low, high);
		int mid = (low + high) / 2;
		if (mid < x)update(key * 2 + 1, mid + 1, high, x, y, value);
		else if (mid >= y)update(key * 2, low, mid, x, y, value);
		else
		{
			update(key * 2, low, mid, x, mid, value);
			update(key * 2 + 1, mid + 1, high, mid + 1, y, value);
		}
		BASE::ans[key] = BASE::op(BASE::ans[key * 2], BASE::ans[key * 2 + 1]);
	}
	void down(int key, int low, int high)
	{
		int mid = (low + high) / 2;
		BASE::ans[key * 2] = type > 2 ? low : opMulti(lazy[key], mid - low + 1);
		BASE::ans[key * 2 + 1] = type > 2 ? high : opMulti(lazy[key], high - mid);
		lazy[key * 2] = lazy[key];
		lazy[key * 2 + 1] = lazy[key];
		lazy[key] = invalid;
	}
	T query(int key, int low, int high, int x, int y)
	{
		if (low == x && high == y)return BASE::ans[key];
		if (lazy[key] != invalid) {
			return type > 2 ? x : opMulti(lazy[key], y - x + 1);
		}
		int mid = (low + high) / 2;
		if (mid < x)return query(key * 2 + 1, mid + 1, high, x, y);
		if (mid >= y)return query(key * 2, low, mid, x, y);
		T a = query(key * 2, low, mid, x, mid);
		T b = query(key * 2 + 1, mid + 1, high, mid + 1, y);
		return BASE::op(a, b);
	}
private:
	T lazy[maxLen * 4 + 10];
};

三，多叉树

四，并查集、DancingLink、无向图、最小生成树


class Union //并查集
{
public:
	Union(int num, bool canZip = true, int startId = 0) //startId一般是0或1,可以大于1,不能太大
	{
		fa.resize(num + startId);
		for (int i = startId; i < fa.size(); i++)fa[i] = i;
		this->canZip = canZip;
		this->startId = startId;
	}
	virtual int find(int x)	//找祖先,canZip控制能否做路径压缩加速
	{
		if (canZip) {
			if (fa[x] == x)return x;
			return fa[x] = find(fa[x]);
		}
		int r = x;
		while (fa[r] != r)r = fa[r];
		return r;
	}
	bool inSame(int x, int y)//是否位于同一个集合
	{
		return find(x) == find(y);
	}
	void merge(int x, int y)//合并2个集合，如果是同一个集合则不做操作
	{
		if (!inSame(x, y))fa[find(x)] = y;
	}
	vector<int> getRoots()//获取所有根节点
	{
		vector<int>ans;
		ans.reserve(fa.size());
		for (int i = startId; i < fa.size(); i++)if (fa[i] == i)ans.push_back(i);
		return ans;
	}
	int getRootNums()//统计根节点数目
	{
		return getRoots().size();
	}
	vector<vector<int>> getGroups()
	{
		vector<int> roots = getRoots();
		map<int, int>m = reflect(roots);
		vector<vector<int>>ans(m.size());
		for (int i = startId; i < fa.size(); i++)ans[m[find(i)]].push_back(i);
		return ans;
	}
protected:
	template<typename T>
	map<T, int> reflect(const vector<T>& v)
	{
		map<T, int>m;
		for (int i = 0; i < v.size(); i++)m[v[i]] = i;
		return m;
	}
protected:
	vector<int>fa;
	bool canZip;
	int startId;
};
class UnionDif :public Union //差分版并查集，依赖路径压缩
{
public:
	UnionDif(int num, int startId = 0) :Union{ num,true,startId } {}
	int find(int x)	//找祖先
	{
		if (fa[x] == x)return x;
		find(fa[x]);
		dif[x] += dif[fa[x]];
		fa[x] = fa[fa[x]];
		return fa[x];
	}
	void merge(int x, int y, double xSubY = 0)//合并2个集合，如果是同一个集合则不做操作
	{
		if (inSame(x, y))return;
		find(x);
		dif[fa[x]] = xSubY - dif[x];
		fa[fa[x]] = y;
		return;
	}
	double getDif(int x)
	{
		return dif[x];
	}
private:
	map<int, double>dif;//每个节点和fa的差分
};
template<typename T>
class Vunion:public Union //集合并查集
{
public:
	Vunion(int num) :Union{ num } {};
	void push(vector<vector<T>>&v) {
		map<T, vector<int>>m;
		for (int i = 0; i < v.size(); i++)for (auto x : v[i])m[x].push_back(i);
		for (auto &p : m) {
			for (auto x : p.second)merge(x, p.second[0]);
		}
	}
};

class DancingLink // 精确覆盖算法
{
public:
	DancingLink(int m, int n, int maxNum) //01矩阵的行、列、1的最大数量
	{
		this->m = m, this->n = n, maxNum += n + 1;
		rhead.resize(m + 1), nums.resize(n + 1);
		row.resize(maxNum), col.resize(maxNum);
		up.resize(maxNum), down.resize(maxNum), lef.resize(maxNum), rig.resize(maxNum);
		sc.resize(m), rows.resize(m);
		for (int i = 0; i <= n; i++)
		{
			up[i] = i, down[i] = i;
			lef[i] = i - 1, rig[i] = i + 1;
			row[i] = 0, col[i] = i, nums[i] = 0;
		}
		lef[0] = n, rig[n] = 0, nums[0] = INT_MAX;
		key = n;
		for (int i = 0; i <= m; i++)rhead[i] = 0;
	}
	void push(int r, int c)//新增坐标在(r,c)的一个节点
	{
		row[++key] = r, col[key] = c;
		up[key] = c, down[key] = down[c];
		up[down[c]] = key, down[c] = key;
		if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
		else
		{
			lef[key] = rhead[r], rig[key] = rig[rhead[r]];
			lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
		}
		nums[c]++;
	}
	vector<vector<int>> getAllAns()
	{
		return dfs(false);
	}
	vector<int> getAnyAns()
	{
		auto v = dfs(true);
		if (v.size())return v[0];
		return vector<int>{};
	}
private:
	vector<vector<int>> dfs(bool onlyOne)
	{
		vector<vector<int>>ans;
		while (true) {
			if (rig[0] == 0) {
				rows.resize(rowsid);
				ans.push_back(rows);
				rows.resize(m);
				if (onlyOne)return ans;
			}
			int c = min_element(nums.begin() + 1, nums.end()) - nums.begin();
			if (rig[0] == 0)c = 0;
			del(c);
			while (true) {
				c = down[c];
				if (c > n)break;
				reback(col[c]);
				if (scid == 0)return ans;
				c = sc[--scid];
				rowsid--;
				for (int j = rig[c]; j != c; j = rig[j])reback(col[j]);
			}
			sc[scid++] = c;//记录选中id
			rows[rowsid++] = row[c];
			for (int j = rig[c]; j != c; j = rig[j])del(col[j]);
		}
		return ans;
	}
	inline void del(int c)//删除第c列的所有元素和他们所在行的所有元素
	{
		lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
		for (int i = down[c]; i != c; i = down[i])
			for (int j = rig[i]; j != i; j = rig[j])
				down[up[j]] = down[j], up[down[j]] = up[j], nums[col[j]]--;
		nums[c] = INT_MAX;
	}
	inline void reback(int c)//完全回退del操作
	{
		lef[rig[c]] = rig[lef[c]] = c, nums[c] = 0;
		for (int i = down[c]; i != c; i = down[i]) {
			for (int j = rig[i]; j != i; j = rig[j])
				down[up[j]] = up[down[j]] = j, nums[col[j]]++;
			nums[c]++;
		}
	}
private:
	int m, n, key;
	vector<int>row, col;//每个节点的行，列
	vector<int>rhead;//每行第一个节点的id
	vector<int>up, down, lef, rig;//每个节点上下左右的节点id
	vector<int>nums;//每一列的元素个数
	vector<int>sc;
	int scid = 0, rowsid = 0;
	vector<int>rows;//覆盖选中的行，值的范围是从1到m
};
template<typename T=int>
struct UndirectedEdge
{
	UndirectedEdge() {
		a = b = dist = 0;
	};
	UndirectedEdge(vector<int>v) {
		a = v[0], b = v[1], dist = v[2];
	}
	int a;//端点a的id
	int b;//端点b的id
	T dist;//ab之间的距离
};
template<typename T=int>
struct UndirectedGraphData
{
public:
	vector<UndirectedEdge<T>>edges; //边集，无法表示孤立点，一条边只出现一次
	map<pair<int, int>, T>edgeMap; //边集，无法表示孤立点，一条边只出现一次
	map<int, vector<int>>adjaList;//邻接表，孤立点是否出现取决于allPointFlag，一条边两个点都出现在对方的邻接表中
	bool allPointFlag=false;//默认邻接表中不含孤立点
	int startId = 0;
public:
    UndirectedGraphData() {
	}
	UndirectedGraphData(const vector<UndirectedEdge<T>>&edges) {
		this->edges = edges;
		adjaList = undirectedEdgeToAdjaList(edges);
		edgeMap = undirectedEdgeToValueMap(edges);
	}
	UndirectedGraphData(const vector<vector<int>>& edges) { //仅限权值为整数的图
		transform(edges.begin(), edges.end(), std::back_inserter(this->edges), [](const vector<int>& v) {return UndirectedEdge<int>{v}; });
		adjaList = undirectedEdgeToAdjaList(this->edges);
		edgeMap = undirectedEdgeToValueMap(this->edges);
	}
	UndirectedGraphData(map<int, vector<int>>& adjaList) { //仅限没有权值的图
		this->adjaList = adjaList;
		for (auto& v : adjaList) {
			for (auto vi : v.second)if (v.first < vi)edges.push_back(UndirectedEdge<T>(vector<int>{v.first, vi, 0}));
		}
		edgeMap = undirectedEdgeToValueMap(edges);
	}
	void setNumV(int n, int startId = 0) { //startId一般是0或1,可以大于1
		allPointFlag = true;
		for (int i = startId; i < startId + n; i++)adjaList[i];
		this->startId = startId;
	}
	int getNumV() const {
		return adjaList.size();
	}
	int getNumE() const {
		return edges.size();
	}
private:
	//输入无向边集{{1，2}{1，3}{2，3}}，输出邻接表{1:{2,3},2:{1,3},3:{1,2}}
	static map<int, vector<int>> undirectedEdgeToAdjaList(const vector<UndirectedEdge<T>>& v)
	{
		map<int, vector<int>> ans;
		for (auto& vi : v) {
			ans[vi.a].push_back(vi.b);
			ans[vi.b].push_back(vi.a);
		}
		return ans;
	}
	//输入无向带权边集，输出边和权的映射
	static map<pair<int, int>, T> undirectedEdgeToValueMap(const vector<UndirectedEdge<T>>& v)
	{
		map<pair<int, int>, T>m;
		for (auto& vi : v) {
			m[{vi.a, vi.b}] = vi.dist;
			m[{vi.b, vi.a}] = vi.dist;
		}
		return m;
	}
};
class UndirectedGraph
{
public:
	//无向拓扑排序，输入无向无环图{{1，2}{1，3}{4，3}}的邻接表和指定根1，输出父节点表{4:3, 3:1, 2:1}
	static map<int, int> undirectedEdgeToFatherList(UndirectedGraphData<int> &g, int root)
	{
		auto& m = g.adjaList;
		map<int, int>visit;
		map<int, int>fa;
		queue<int>q;
		q.push(root);
		visit[root] = 1;
		while (!q.empty()) {
			int id = q.front();
			q.pop();
			for (auto c : m[id]) {
				if (visit[c] == 0)q.push(c), fa[c] = id;
				visit[c] = 1;
			}
		}
		return fa;
	}
	//根据无向图的邻接表判断是否有环
	static bool hasCircle(const UndirectedGraphData<int>& g)
	{
		auto& m = g.adjaList;
		vector<int>keys; //auto keys = getFirst(m);
		transform(m.begin(), m.end(), std::back_inserter(keys), [](const pair<int, vector<int>>& p) {return p.first; });
		int minkey = *min_element(keys.begin(), keys.end());
		int maxKey = *max_element(keys.begin(), keys.end());
		Union unions(maxKey - minkey + 1);
		map<pair<int, int>, int>mp;
		for (auto& mi : m) {
			for (auto k : mi.second) {
				if (mp[make_pair(k, mi.first)])continue;
				if (unions.inSame(k - minkey, mi.first - minkey))return true;
				unions.merge(k - minkey, mi.first - minkey);
				mp[make_pair(mi.first, k)] = 1;
			}
		}
		return false;
	}
	//给定一个2n个点的图，选出n条边，刚好覆盖这2n个点
	static vector<vector<UndirectedEdge<int>>> getEdgeCover(int n, UndirectedGraphData<int>& g)
	{
		auto& v = g.edges;
		DancingLink d(v.size(), n * 2, v.size() * 2);
		for (int i = 0; i < v.size(); i++) {
			d.push(i, v[i].a + 1);
			d.push(i, v[i].b + 1);
		}
		vector<vector<UndirectedEdge<int>>>ans;
		vector<vector<int>> vrow = d.getAllAns();
		for (auto vi : vrow) {
			vector<UndirectedEdge<int>>vans; //getNumFromId(v, vi)
			transform(vi.begin(), vi.end(), std::back_inserter(vans), [&](int id) {return v[id]; });
			ans.push_back(vans);
		}
		return ans;
	}
};
class Kruskal
{
public:
	//计算最小生成树，结果按照边从小到大排序,出参treeNum是森林中树的数量
	static vector<UndirectedEdge<int>> minCostConnectPoints(int n, vector<UndirectedEdge<int>>& v, int& treeNum)
	{
		sort(v.begin(), v.end(), cmp);
		Union unions(n);
		vector<UndirectedEdge<int>>ans;
		for (int i = 0, j = 0; j < n - 1 && i < v.size(); i++)
		{
			if (unions.inSame(v[i].a, v[i].b))continue;
			unions.merge(v[i].a, v[i].b);
			ans.push_back(v[i]);
			j++;
		}
		treeNum = unions.getRootNums();
		return ans;
	}
private:
	static bool cmp(UndirectedEdge<int>& a, UndirectedEdge<int>& b)
	{
		return a.dist < b.dist;
	}
};
class Prim
{
public:
	//计算最小生成树，结果按照边从小到大排序
	static vector<pair<int, int>> minCostConnectPoints(int n, map<pair<int, int>, int>& value)
	{
		vector<bool>visit_(n);
		vector<int>minLen(n);
		for (int i = 0; i < n; i++) {
			minLen[i] = INT_MAX;
			visit_[i] = false;
		}
		minLen[getStartId(n, value)] = INT_MIN;
		vector<pair<int, int>>ans;
		for (int i = 0; i < n; i++) {
			int id = getId(n, visit_, minLen);
			for (int j = 0; j < n; j++) {
				if (visit_[j] && value[make_pair(id, j)] == minLen[id]) {
					ans.push_back(make_pair(id, j));
					break;
				}
			}
			visit_[id] = true;
			fresh(n, visit_, minLen, value, id);
		}
		return ans;
	}
private:
	static int getStartId(int n, map<pair<int, int>, int>& value)
	{
		int m = INT_MAX;
		int ans = 0;
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				if (i != j && m > value[make_pair(i, j)]) {
					m = value[make_pair(i, j)];
					ans = i;
				}
			}
		}
		return ans;
	}
	static int getId(int n, vector<bool>& visit_, vector<int>& minLen)
	{
		int m = INT_MAX;
		int ans = 0;
		for (int i = 0; i < n; i++) {
			if (!visit_[i] && m > minLen[i]) {
				m = minLen[i];
				ans = i;
			}
		}
		return ans;
	}
	static void fresh(int n, vector<bool>& visit_, vector<int>& minLen, map<pair<int, int>, int>& value, int id)
	{
		for (int i = 0; i < n; i++) {
			if (!visit_[i])minLen[i] = min(minLen[i], value[make_pair(i, id)]);
		}
	}
};

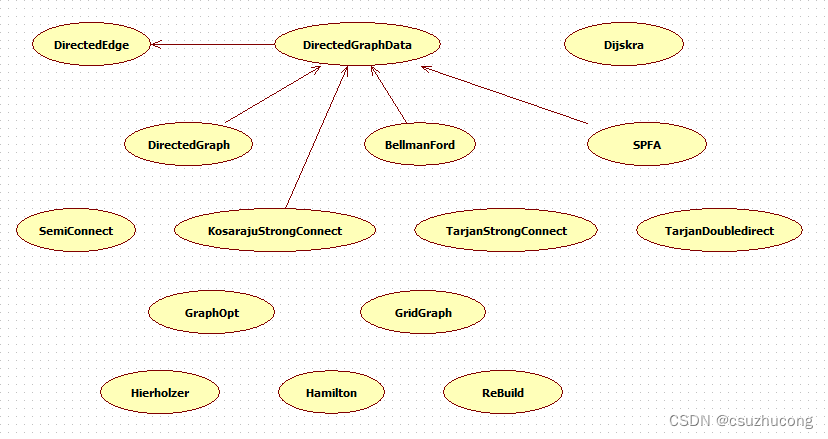
五，有向图、单源最短路径、连通分量、拓扑排序


template<typename T = int>
struct DirectedEdge
{
	DirectedEdge() {
		a = b = dist = 0;
	};
	DirectedEdge(vector<int>v) {
		a = v[0], b = v[1], dist = v[2];
	}
	int a;//端点a的id
	int b;//端点b的id
	T dist;//从a到b的距离
};
template<typename T = int>
struct DirectedGraphData
{
public:
	vector<DirectedEdge<T>>edges; //边集，无法表示孤立点
	map<pair<int, int>, T>edgeMap; //边集，无法表示孤立点
	map<int, vector<int>>adjaList;//邻接表，孤立点是否出现取决于allPointFlag
	bool allPointFlag = false;//默认邻接表中不含孤立点
	int startId = 0;
public:
    DirectedGraphData(){
	}
	DirectedGraphData(const vector<DirectedEdge<T>>& edges) {
		this->edges = edges;
		adjaList = directedEdgeToAdjaList(edges);
		edgeMap = directedEdgeToValueMap(edges);
	}
	DirectedGraphData(const vector<vector<int>>& edges) { //仅限权值为整数的图
		transform(edges.begin(), edges.end(), std::back_inserter(this->edges), [](const vector<int>& v) {return DirectedEdge<int>{v}; });
		adjaList = directedEdgeToAdjaList(this->edges);
		edgeMap = directedEdgeToValueMap(this->edges);
	}
	DirectedGraphData(map<int, vector<int>>& adjaList) { //仅限没有权值的图
		this->adjaList = adjaList;
		for (auto& v : adjaList) {
			for (auto vi : v.second)edges.push_back(DirectedEdge<T>({v.first, vi, 0}));
		}
		edgeMap = directedEdgeToValueMap(edges);
	}
	void setNumV(int n, int startId = 0) { //startId一般是0或1,可以大于1
		allPointFlag = true;
		for (int i = startId; i < startId + n; i++)adjaList[i];
		this->startId = startId;
	}
	int getNumV() const {
		return adjaList.size();
	}
	int getNumE() const {
		return edges.size();
	}
private:
	//输入有向边集{{1，2}{1，3}{2，3}}，输出邻接表{1:{2,3},2:{3}}
	static map<int, vector<int>> directedEdgeToAdjaList(const vector<DirectedEdge<T>>& v)
	{
		map<int, vector<int>> ans;
		for (auto& vi : v) {
			ans[vi.a].push_back(vi.b);
			ans[vi.b];
		}
		return ans;
	}
	//输入有向带权边集，输出边和权的映射
	static map<pair<int, int>, int> directedEdgeToValueMap(const vector<DirectedEdge<T>>& v)
	{
		map<pair<int, int>, int>m;
		for (auto& vi : v) {
			m[{vi.a, vi.b}] = vi.dist;
		}
		return m;
	}
};
class DirectedGraph
{
public:
	//构建有向图的反向图
	static map<int, vector<int>> reverseGraph(const DirectedGraphData<int> &g)
	{
		auto& m = g.adjaList;
		map<int, vector<int>> ans;
		for (auto& mi : m) {
			for (auto& k : mi.second)ans[k].push_back(mi.first);
		}
		return ans;
	}
	//求有向无环图中的最长路径长度，出参nextNode是每个点的后继,len是每个点出发的最长路径长度
	static int getLongestPath(map<int, vector<int>>& m, map<int, int>& nextNode, map<int, int>& len)
	{
		int ans = 0;
		for (auto& ai : m)ans = max(ans, dp(m, nextNode, len, ai.first));
		return ans;
	}
	//判断是否有环
	static bool hasCircle(int numCourses, map<int, vector<int>>& m)
	{
		map<int, int>visitt;//单次访问标记
		map<int, int>flag;//所有访问标记
		for (int i = 0; i < numCourses; i++)
		{
			if (flag[i])continue;
			if (!canFinish(m, i, visitt, flag))return true;
		}
		return false;
	}

private:
	static int dp(map<int, vector<int>>& m, map<int, int>& nextNode, map<int, int>& len, int id)
	{
		if (len[id])return len[id];
		len[id] = 1, nextNode[id] = -1; //无后继的则是 - 1
		for (auto k : m[id]) {
			if (len[id] < dp(m, nextNode, len, k) + 1) {
				len[id] = dp(m, nextNode, len, k) + 1;
				nextNode[id] = k;
			}
		}
		return len[id];
	}
	static bool canFinish(map<int, vector<int>>& m, int loc, map<int, int>& visitt, map<int, int>& flag) {
		if (visitt[loc] == 1)return false;
		if (flag[loc] == 1)return true;
		visitt[loc] = 1, flag[loc] = 1;
		for (int k : m[loc])if (!canFinish(m, k, visitt, flag))return false;
		visitt[loc] = 0;
		return true;
	}
};
class Dijskra//求最短路,适用于不存在负权值的边的图
{
public:
	static map<int, int> shortestPath(map<int, vector<int>>& m, map<pair<int, int>, int>& value, int n, int src)
	{
		map<int, int>dis;
		priority_queue< Node, vector< Node>, cmp>que;
		map<int, int>visit;
		for (int i = 0; i < n; i++)dis[i] = INT_MAX;
		que.push({ src,0 });
		dis[src] = 0;
		while (!que.empty())
		{
			Node nod = que.top();
			que.pop();
			if (visit[nod.id])continue;
			visit[nod.id] = 1;
			for (auto& vi : m[nod.id]) {
				if (nod.len + value[{nod.id, vi}] < dis[vi]) {
					que.push({ vi, dis[vi] = nod.len + value[{nod.id, vi}] });
				}
			}
		}
		return dis;
	}
private:
	struct Node
	{
		int id;
		int len;
	};
	class cmp
	{
	public:
		bool operator()(Node a, Node b)
		{
			return a.len > b.len;
		}
	};
};
class BellmanFord //求最短路,适用于不存在负权值的环的图
{
public:
	static map<int, int> shortestPath(const DirectedGraphData<int>& g, int src)
	{
		map<int, int>dis;
		int n = g.getNumV();
		for (int i = 0; i < n; i++)dis[i] = INT_MAX;
		dis[src] = 0;
		for (int i = 0; i < n; i++) {
			if (!refresh(g.edgeMap, dis))break;
			if (i == n - 1)return map<int, int>{}; //有负环
		}
		return dis;
	}
private:
	static inline bool refresh(const map<pair<int, int>, int>& value, map<int, int>&dis)
	{
		bool flag = false;
		auto dis2 = dis;
		for (auto& e : value) {
			if (dis2[e.first.second] > ((long long)dis[e.first.first]) + e.second) {
				dis2[e.first.second] = ((long long)dis[e.first.first]) + e.second, flag = true;
			}
		}
		dis = dis2;
		return flag;
	}
};
class SPFA //求最短路,适用于不存在负权值的环的图
{
public:
	static map<int, int> shortestPath(const DirectedGraphData<int>& g, int src)
	{
		map<int, int>dis;
		map<int, bool>inQueue;
		map<int, int>visit;
		int n = g.getNumV();
		for (int i = 0; i < n; i++)dis[i] = INT_MAX;
		dis[src] = 0;
		queue<int>q;
		q.push(src);
		visit[src]++;
		inQueue[src] = true;
		while (!q.empty()) {
			int t = q.front();
			q.pop();
			inQueue[t] = false;
			auto v = refresh(dis, t, g);
			for (auto vi : v) {
				if (inQueue[vi])continue;
				q.push(vi);
				inQueue[vi] = true;
				if (++visit[vi] >= n)return map<int, int>{};//存在负环
			}
		}
		return dis;
	}
private:
	static inline vector<int> refresh(map<int, int>&dis, int t, const DirectedGraphData<int>& g)
	{
		vector<int>ans;
		auto it = g.adjaList.find(t);
		if (it == g.adjaList.end())return ans;
		long long d = dis[t];
		for (auto vi : it->second) {
			if (dis[vi] > d + g.edgeMap.at(make_pair(t, vi))) {
				dis[vi] = d + g.edgeMap.at(make_pair(t, vi));
				ans.push_back(vi);
			}
		}
		return ans;
	}
};
//不区分有向图和无向图的通用操作
class GraphOpt
{
public:
	//根据点集取子图,输入邻接表，输出邻接表
	static map<int, vector<int>> getSubGraph(map<int, vector<int>>& m, vector<int>& v)
	{
		map<int, vector<int>>ans;
		map<int, int>mv;
		for (auto vi : v)mv[vi] = 1;
		for (auto vi : v) {
			for (auto mi : m[vi]) {
				if (mv[mi])ans[vi].push_back(mi);
			}
		}
		return ans;
	}
};
class SemiConnect
{
public:
	//半连通分量分割
	static vector<vector<int>> semiConnectComponent(map<int, vector<int>>& m)
	{
		vector<vector<int>>allans;
		map<int, int>visit;
		for (auto& mi : m) {
			int k = mi.first;
			if (visit[k])continue;
			vector<int>ans;
			DFS(m, visit, k, ans);
			allans.push_back(ans);
		}
		return allans;
	}
protected:
	//DFS从k开始遍历，记录所有节点最后一次访问的顺序的反序
	static void DFS(map<int, vector<int>>& m, map<int, int>& visit, int k, vector<int>& ans)
	{
		if (visit[k])return;
		visit[k] = 1;
		for (auto i : m[k])DFS(m, visit, i, ans);
		ans.insert(ans.begin(), k);
	}
};
class KosarajuStrongConnect :public DirectedGraph, public GraphOpt, public SemiConnect
{
public:
	//Kosaraju算法，强连通分量分割
	static vector<vector<int>> connectComponent(map<int, vector<int>>& m)
	{
		vector<vector<int>> semi = semiConnectComponent(m);
		auto m2 = reverseGraph(m);
		vector<vector<int>>allans;
		map<int, int>visit;
		for (auto& s : semi) {
			auto m3 = getSubGraph(m2, s);
			for (auto& k : s) {
				if (visit[k])continue;
				vector<int>ans;
				DFS(m3, visit, k, ans);
				allans.push_back(ans);
			}
		}
		return allans;
	}
	//强连通分量缩点，输入强连通分量列表，输出缩点后的邻接表
	static map<int, vector<int>> getPointGraph(vector<vector<int>>&v, map<int, vector<int>>&m)
	{
		map<int, int>g;
		map<int, vector<int>>ans;
		for (int i = 0; i < v.size(); i++)for (auto x : v[i])g[x] = i;
		for (auto &mi : m) {
			for (auto x : mi.second)
				if (g[x] != g[mi.first])
					ans[mi.first].push_back(x);
		}
		return ans;
	}
};
class TarjanDoubledirect
{
public:
	vector<pair<int, int>>cutb;//割边
	vector<int>cutv;//割点
	vector<vector<int>>conv;//点双连通分量的点集
	vector<vector<long long>>convb;//点双连通分量的边集
	int cons = 0;//无向连通分量数目
	TarjanDoubledirect(int n, map<int, vector<int>>& m)
	{
		this->n = n;
		this->m = m;
		visit.resize(n);
		added.resize(n);
		dfn.resize(n);
		low.resize(n);
		for (int i = 0; i < n; i++)if (!visit[i]) {
			root = i;
			dfs(i);
			cons++;
		}
		FillConv();
	}
private:
	void dfs(int k)
	{
		visit[k] = true;
		low[k] = dfn[k] = dfnId++;
		bool cv = false;
		int chNum = 0;
		st.push(k);
		for (auto nk : m[k]) {
			if (isBackB(nk))low[k] = min(low[k], dfn[nk]);
			if (visit[nk])continue;
			chNum++;
			sFa.push(k);
			dfs(nk);
			sFa.pop();
			low[k] = min(low[k], low[nk]);
			vector<int>conv1;
			vector<long long>convb1;
			if (low[nk] >= dfn[k]) {
				cv = true;
				for (int time = INT_MAX; time; time--) {
					if (st.top() == nk)time = 1;
					conv1.push_back(st.top());
					added[st.top()] = true;
					for (auto i : m[st.top()])if (!added[i])convb1.push_back((long long)(st.top()) * n + i);
					st.pop();
				}
				if (conv1.size() > 1) {
					conv1.push_back(k);
					conv.push_back(conv1);
					convb.push_back(convb1);
				}
			}
			if (low[nk] >= dfn[nk])cutb.push_back(make_pair(k, nk));
		}
		if ((k != root && cv && chNum > 0) || (k == root && chNum > 1))cutv.push_back(k);
	}
	bool isBackB(int nk) // 判断从k到nk是不是后向边
	{
		return visit[nk] && (sFa.empty() || nk != sFa.top());//如果st.top()是nk，则是树边，不是后向边
	}
	void FillConv()//补充由单点组成的点连通分量
	{
		map<int, int>m;
		for (auto& ci : conv) {
			for (auto& k : ci)m[k] = 1;
		}
		vector<int>conv1(1);
		for (int i = 0; i < n; i++)if (m[i] == 0) {
			conv1[0] = i;
			conv.push_back(conv1);
			convb.push_back(vector<long long>());
		}
	}
	int n;
	int dfnId = 0;
	int root;
	vector<bool>visit;//DFS访问标记
	vector<bool>added;
	vector<int>dfn;//首次访问的次序
	vector<int>low;//通过一条后向边能达到的最小dfn
	map<int, vector<int>> m;//邻接表
	stack<int>sFa;//用于判断父节点
	stack<int>st;
};
class TarjanStrongConnect
{
public:
	vector<vector<int>>conv;//强连通分量的点集
	TarjanStrongConnect(int n, map<int, vector<int>>& m)
	{
		this->n = n;
		this->m = m;
		visit.resize(n);
		added.resize(n);
		dfn.resize(n);
		low.resize(n);
		for (int i = 0; i < n; i++)if (!visit[i]) {
			root = i;
			dfs(i);
		}
		FillConv();
	}
private:
	void dfs(int k)
	{
		visit[k] = true;
		low[k] = dfn[k] = dfnId++;
		bool cv = false;
		int chNum = 0;
		st.push(k);
		for (auto nk : m[k]) {
			if (isBackB(nk))low[k] = min(low[k], dfn[nk]);
			if (visit[nk])continue;
			chNum++;
			dfs(nk);
			low[k] = min(low[k], low[nk]);
		}
		vector<int>conv1;
		vector<long long>convb1;
		if (low[k] >= dfn[k]) {
			cv = true;
			for (int time = INT_MAX; time; time--) {
				if (st.top() == k)time = 1;
				conv1.push_back(st.top());
				added[st.top()] = true;
				st.pop();
			}
			conv.push_back(conv1);
		}
	}
	bool isBackB(int nk) // 判断从k到nk是不是后向边
	{
		return visit[nk] && !added[nk];
	}
	void FillConv()//补充由单点组成的点连通分量
	{
		map<int, int>m;
		for (auto& ci : conv) {
			for (auto& k : ci)m[k] = 1;
		}
		vector<int>conv1(1);
		for (int i = 0; i < n; i++)if (m[i] == 0) {
			conv1[0] = i;
			conv.push_back(conv1);
		}
	}
	int n;
	int dfnId = 0;
	int root;
	vector<bool>visit;//DFS访问标记
	vector<bool>added;
	vector<int>dfn;//首次访问的次序
	vector<int>low;//通过一条后向边能达到的最小dfn
	map<int, vector<int>> m;//邻接表
	stack<int>st;
};
//有向图拓扑排序
class DirectedTopoSort:public KosarajuStrongConnect
{
public:
	//有向无环图拓扑排序，输入n=3，g.edges={{0,1}{0,2}{1,2}}, 输出{0,1,2}，有环则输出为空
	static vector<int> topoSortNoCircle(int n, DirectedGraphData<int>& g)
	{
		auto& v = g.edges;
		priority_queue<int, vector<int>, greater<int>> q;
		map<int, int>m;
		for (auto &vi : v)m[vi.b]++;
		for (int i = 0; i < n; i++)if (m[i] == 0)q.push(i);
		vector<int>ans;
		auto &mv = g.adjaList;
		while (!q.empty()) {
			int k = q.top();
			q.pop();
			ans.push_back(k);
			for (auto i : mv[k]) {
				m[i]--;
				if (m[i] == 0)q.push(i);
			}
		}
		return ans.size() == n ? ans : vector<int>{};
	}
	//有向图拓扑排序
	static vector<vector<int>> topoSort(DirectedGraphData<int>& g)
	{
		vector<vector<int>> con = connectComponent(g.adjaList);
		map<int, vector<int>> pointGraph = getPointGraph(con, g.adjaList);
		DirectedGraphData<int>ga(pointGraph);
		vector<int> vp = topoSortNoCircle(con.size(), ga);
		vector<vector<int>>ans;
		for (auto id : vp)ans.push_back(con[id]);
		return ans;
	}
};

六，网格图、回路链路、路径重建


class GridGraph
{
public:
	GridGraph(int row, int col)
	{
		this->row = row;
		this->col = col;
		initD4D8();
	}
	int gridId(int r, int c) //阅读顺序的id,先给col赋值再调用
	{
		return r * col + c;
	}
	vector<int> getNeighbor4(int k)//获得四邻居的id
	{
		vector<int>ans;
		for (int i = 0; i < 4; i++) {
			if (inBoard(k / col + dx4[i], k % col + dy4[i]))ans.push_back(k + d4[i]);
		}
		return ans;
	}
	vector<int> getNeighbor8(int k)//获得八邻居的id
	{
		vector<int>ans;
		for (int i = 0; i < 8; i++) {
			if (inBoard(k / col + dx8[i], k % col + dy8[i]))ans.push_back(k + d8[i]);
		}
		return ans;
	}
private:
	int row;
	int col;
	//二维坐标系的邻居偏移量
	const vector<int> dx4{ 0,0,1,-1 };
	const vector<int> dy4{ 1,-1,0,0 };
	const vector<int> dx8{ 0,0,1,-1,1,1,-1,-1 };
	const vector<int> dy8{ 1,-1,0,0 ,1,-1,1,-1 };
	//一维id坐标系的邻居偏移量
	vector<int> d4;
	vector<int> d8;
private:
	inline void initD4D8()
	{
		for (int i = 0; i < 4; i++)d4.push_back(gridId(dx4[i], dy4[i]));
		for (int i = 0; i < 8; i++)d8.push_back(gridId(dx8[i], dy8[i]));
	}
	inline bool inBoard(int r, int c)
	{
		return r >= 0 && r < row&& c >= 0 && c < col;
	}
	inline bool inBoard(int id)
	{
		return id >= 0 && inBoard(id / col, id % col);
	}
};
class Hierholzer {
public:
	stack<int>euler;//欧拉回路或链路,栈顶是起点
	Hierholzer(int n, map<int, vector<int>>& m, int type, int start = 0)//type=0是无向图 1是有向图
	{
		this->n = n;
		this->m = m;
		this->type = type;
		dfs(GetStartPoint(start));
	}
private:
	int GetStartPoint(int start)//链路是唯一起点，回路是指定起点
	{
		if (type == 0) {
			for (auto& mi : m) {
				if (mi.second.size() % 2)return mi.first;
				for (auto nk : mi.second)num[id(mi.first, nk)]++;
			}
			for (auto& ni : num)ni.second /= 2;
		}
		else {
			map<int, int>m2;
			for (auto& mi : m)for (auto nk : mi.second)m2[nk]++, num[id(mi.first, nk)]++;
			for (auto& mi : m)if (mi.second.size() > m2[mi.first])return mi.first;
		}
		return start;
	}
	void dfs(int k)
	{
		while (true) {
			while (mid[k] < m[k].size()) {
				if (num[id(k, m[k][mid[k]])]-- <= 0)mid[k]++;
				else sdfs.push(k), k = m[k][mid[k]];
			}
			euler.push(k);
			if (sdfs.empty()) return;
			k = sdfs.top(), sdfs.pop();
		}
	}
	inline long long id(int a, int b)
	{
		if (type == 0 && a > b)a ^= b ^= a ^= b;
		return (long long)a * n + b;
	}
	int n;
	int type;
	stack<int>sdfs;
	map<int, vector<int>> m;//邻接表
	map<int, int>mid;
	map<long long, int>num;//支持多重边
};
class Hamilton
{
public:
	stack<int> hami;//哈密顿链路
	Hamilton(int n, map<int, vector<int>>& m, int type)//type=0是无向图 1是有向图
	{
		this->n = n;
		this->m = m;
		this->type = type;
		for (int i = 0; i < n; i++)dfs(i);
	}
private:
	bool dfs(int k)
	{
		s.push(k);
		if (s.size() == n) {
			hami = s;
			return true;
		}
		for (auto nk : m[k]) {
			if (visit[k])continue;
			visit[k] = 1;
			if (dfs(nk))return true;
			visit[k] = 0;
		}
		s.pop();
		return false;
	}
	int n;
	int type;
	map<int, vector<int>> m;//邻接表
	map<int, int>visit;
	stack<int>s;
};
class ReBuild
{
public:
	stack<int> ans;
	ReBuild(map<int, int>& dis, map<int, vector<int>>& m, int col, int s, int e)
	{
		this->e = e;
		this->col = col;
		ans.push(e);
		dfs(dis, m, s);
	}
private:
	bool dfs(map<int, int>& dis, map<int, vector<int>>& m, int k)
	{
		if (k == e)return true;
		for (int nex : m[k]) {
			if (dis[nex] == dis[k] + len(k, nex) && dfs(dis, m, nex)) {
				ans.push(k);
				return true;
			}
		}
		return false;
	}
	int len(int s, int e)
	{
		if (s / col == e / col)return abs(s - e);
		return abs(s - e) / col;
	}
	int col;
	int e;
};

七，test


template<typename T>
static bool isSame(const vector<T>& v1, const vector<T>& v2)
{
	if (v1.size() - v2.size())return false;
	for (int i = 0; i < v1.size(); i++)if (v1[i] != v2[i])return false;
	return true;
}
#define EXPECT_VEC_EQ(a,b) if(!isSame((a),(b))){cout<<"ERROR!!!!!!!!!\n";return false;}
#define EXPECT_EQ(a,b) if(a!=b){cout<<"ERROR!!!!!!!!!\n";return false;}


bool test1()
{
	TreeNode t1(1), t2(2), t3(3), t4(4);
	t1.left = &t2, t1.right = &t3, t2.left = &t4;
	auto p = &t1;
	EXPECT_EQ(MaxDepth(p), 3);
	EXPECT_EQ(MinDepth(p), 2);
	vector<int>pre{ 1, 2, 4, 3 }, post{ 4, 2, 3, 1 }, inorder{ 4, 2, 1, 3 };
	EXPECT_VEC_EQ(PreorderTraversal(p), pre);
	EXPECT_VEC_EQ(PostorderTraversal(p), post);
	EXPECT_VEC_EQ(InorderTraversal(p), inorder);
	auto p2 = BuildTree(pre, inorder);
	EXPECT_EQ(IsSameTree(p, p2), true);
	p2 = BuildTree2(inorder, post);
	EXPECT_EQ(IsSameTree(p, p2), true);
	EXPECT_EQ(CountNodes(p), 4);
	p2 = CopyTree(p);
	EXPECT_EQ(IsSameTree(p, p2), true);
	InvertTree(p2);
	EXPECT_EQ(IsSameTree(p, p2), false);
	InvertTree(p2);
	EXPECT_EQ(IsSameTree(p, p2), true);
	return true;
}

bool testTreeArray()
{
	TreeArray<> t(100);
	t.add(1, 5);
	t.add(3, 10);
	EXPECT_EQ(t.getSum(1), 5);
	EXPECT_EQ(t.getSum(100), 15);
	return true;
}
bool testSegmentTree()
{
	SegmentTreeTypeSum<10000> st;
	int *num = st.getData();
	num[1] = 3, num[2] = 4, num[3] = 2, num[4] = 6;
	st.build(4);
	st.update(1, 5); //5 4 2 6
	EXPECT_EQ(st.query(1, 3), 11);
	EXPECT_EQ(st.queryPreSum(5), 1);
	EXPECT_EQ(st.queryPreSum(9), 2);
	EXPECT_EQ(st.queryPreSum(11), 3);
	SegmentTree<1, 10000> stMin;
	num = stMin.getData();
	num[1] = 3, num[2] = 4, num[3] = 2, num[4] = 6;
	stMin.build(4);
	stMin.update(2, 3, 5);//3 5 5 6
	EXPECT_EQ(stMin.query(1, 4), 3);
	EXPECT_EQ(stMin.query(3, 4), 5);
	return true;
}
bool test2()
{
	return testTreeArray() && testSegmentTree();
}

bool test3() //待完善
{
    MultiTree{};
	return true;
}

bool testUnion()
{
	Union u(5);
	EXPECT_VEC_EQ(u.getRoots(), (vector<int>{0, 1, 2, 3, 4}));
	u.merge(1, 2);
	u.merge(1, 1);
	u.merge(3, 3);
	EXPECT_VEC_EQ(u.getRoots(), (vector<int>{0, 2, 3, 4}));
	u.merge(4, 3);
	auto v = u.getRoots();
	EXPECT_VEC_EQ(u.getRoots(), (vector<int>{0, 2, 3}));
	return true;
}
bool testDancingLink()//待完善
{
	return true;
}

bool testUndirectedGraph()//待完善
{
	return true;
}
bool testKruskal()//待完善
{
	Kruskal{};
	return true;
}
bool testPrim()//待完善
{
	Prim{};
	return true;
}
bool test4()
{
	return testUnion() && testDancingLink() && testUndirectedGraph() && testKruskal() && testPrim();
}

bool testDirectedGraph()//待完善
{
	DirectedGraph{};
	return true;
}
bool testDijskra()//待完善
{
	map<int, vector<int>> m;
	map<pair<int, int>, int> value;
	int n = 1;
	DijskraShortestPath(m, value, n, 0);
	return true;
}
bool testBellmanFord()//待完善
{
	return true;
}
bool testGraphOpt()//待完善
{
	GraphOpt{};
	return true;
}
bool testConnect()//待完善
{
	SemiConnect{};
	KosarajuStrongConnect{};
	int n = 1;
	map<int, vector<int>> m;
	TarjanDoubledirect{ n,m };
	TarjanStrongConnect{ n,m };
	return true;
}
bool testTopoSort() //待完善
{
	map<int, vector<int>>m;
	m[1].push_back(2);
	m[2].push_back(3);
	m[3].push_back(1);
	m[3].push_back(4);
	m[4].push_back(5);
	m[5].push_back(6);
	m[6].push_back(4);
	m[5].push_back(7);
	DirectedGraphData<int>g(m);
	auto ans = DirectedTopoSort::topoSort(g);
	return true;
}
bool test5()
{
	return testDirectedGraph() && testDijskra() && testBellmanFord() && testGraphOpt() && testConnect() && testTopoSort();
}

bool testGridGraph()//待完善
{
	GridGraph{ 0, 0 };
	return true;
}

bool testHierholzerAndHamilton()//待完善
{
	map<int, vector<int>> m;
	map<pair<int, int>, int> value;
	int n = 1;
	Hierholzer{ n,m,0,0 };
	Hamilton{ n,m,0 };
	return true;
}
bool testReBuild()//待完善
{
	map<int, vector<int>> m;
	map<int, int> dis;
	ReBuild{ dis,m,0,0,0 };
	return true;
}
bool test6()
{
	return testGridGraph() && testHierholzerAndHamilton() && testReBuild();
}

bool hasCircleWithOne(vector<vector<int>>& matrix)
{
	GridGraph opt(matrix.size(), matrix[0].size());
	map<int, vector<int>>m;
	for (int i = 1; i < matrix.size(); i++)for (int j = 0; j < matrix[0].size(); j++)
		if (matrix[i][j] == 1 && matrix[i - 1][j] == 1)
			m[opt.gridId(i, j)].push_back(opt.gridId(i - 1, j)), m[opt.gridId(i - 1, j)].push_back(opt.gridId(i, j));
	for (int i = 0; i < matrix.size(); i++)for (int j = 1; j < matrix[0].size(); j++)
		if (matrix[i][j] == 1 && matrix[i][j - 1] == 1)
			m[opt.gridId(i, j)].push_back(opt.gridId(i, j - 1)), m[opt.gridId(i - 1, j)].push_back(opt.gridId(i, j));
	return HasUndirectedCircle(m);
}
bool testHasCircleWithOne()//待完善
{
	vector<vector<int>>v{ {1,0},{1,1} };
	EXPECT_EQ(hasCircleWithOne(v), false);
	v[0][1] = 1;
	EXPECT_EQ(hasCircleWithOne(v), true);
	return true;
}

int main()
{
	if (test1() && test2() && test3() && test4() && test5() && test6() && testHasCircleWithOne())cout << "test succ!";
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1008722.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

关于 Resolution（分辨率、解析力）各单位的意义及相互之间的换算

关于 Resolution（分辨率、解析力）各单位的意义及相互之间的换算

1、问题背景 最近在调试的项目&#xff0c;有关于对解析力的要求&#xff0c;用 imatest 软件测试 MTF50 的值&#xff0c;如下图所示&#xff0c;可以看到他有不同的单位表示&#xff0c;LW/PH、Cycles/pixel 。另外关于解析力的单位还有LP/mm、L/mm、Cycles/mm、LP/PH&#…
阅读更多...
学生护眼灯用白炽灯还是led？专业的学生护眼灯推荐

学生护眼灯用白炽灯还是led？专业的学生护眼灯推荐

现在的护眼灯逐渐成为了孩子们学习路上必不可少的一盏灯具&#xff0c;它比普通的台灯光线更加均匀舒适&#xff0c;而且更加护眼。因此也成为了家长们呵护孩子视力健康的一大“帮手”&#xff0c;不过护眼台灯的种类也有很多&#xff0c;最近就有家长问孩子使用的护眼灯是白炽…
阅读更多...
用GPT干的18件事，能够真正提高学习生产力，建议收藏

用GPT干的18件事，能够真正提高学习生产力，建议收藏

用GPT干的18件事&#xff0c;能够真正提高学习生产力&#xff0c;建议收藏。 语法更正 文本翻译 语言转换 代码解释 修复代码错误 作为百科全书 信息提取 好友聊天 创意生成器 采访问题 论文大纲 故事创作 问题类比 创建 SQL 需求 情感分析 将产品描述转变为广告 关键字提取 闲…
阅读更多...
Tailwind CSS 初学者指南

Tailwind CSS 初学者指南

Tailwind CSS是一个实用程序优先的CSS框架&#xff0c;允许您快速构建现代网站&#xff0c;而无需离开HTML。它是 Web 开发社区中最流行和使用最广泛的 CSS 框架之一&#xff0c;每月下载量超过 250 万次1。在本文中&#xff0c;我们将探讨 Tailwind CSS 2023 的路线图&#xf…
阅读更多...
go string类型简叙

go string类型简叙

字符串赋值后就不能修改 var str string "abcd" str[0] f //这里就有能修改str内容字符串的两种表示形式 双引号&#xff0c;会识别转义字符反引号&#xff0c;以字符串的原生形式输出&#xff0c;包括换行和特殊字符&#xff0c;可以实现防止攻击、输出输出源代…
阅读更多...
el-table表格中加入输入框

el-table表格中加入输入框

<template><div class"box"><div class"btn"><el-button type"primary">发送评委</el-button><el-button type"primary" click"flag true" v-if"!flag">编辑</el-button…
阅读更多...
Android EditText筛选+选择功能开发

Android EditText筛选+选择功能开发

在日常开发中经常会遇到这种需求&#xff0c;EditText既需要可以筛选&#xff0c;又可以点击选择。这里筛选功能用的是AutoCompleteTextView&#xff0c;选择功能使用的是第三方库https://github.com/kongzue/DialogX。 Android AutoCompleteTextView(自动完成文本框)的基本使用…
阅读更多...
Mozilla 紧急修补 Firefox 和 Thunderbird 中的 WebP 严重零日漏洞

Mozilla 紧急修补 Firefox 和 Thunderbird 中的 WebP 严重零日漏洞

Mozilla 周二发布了安全更新&#xff0c;修复了 Firefox 和 Thunderbird 中的一个关键零日漏洞。 该漏洞被标记为 CVE-2023-4863&#xff0c;是 WebP 图像格式中的堆缓冲区溢出漏洞&#xff0c;在处理特制图像时可能导致任意代码执行。 Mozilla 在一份公告中说&#xff0c;打…
阅读更多...
MyBatisPlus（二）基础Mapperr接口：增删改查

MyBatisPlus（二）基础Mapperr接口：增删改查

MyBatisPlus&#xff1a;基础Mapper接口&#xff1a;增删改查 插入一条数据 代码 Testpublic void insert() {User user new User();user.setId(6L);user.setName("张三");user.setAge(25);user.setEmail("zhangsanexample.com");userMapper.insert(use…
阅读更多...
系统安全漏洞检测技术第三方检测机构

系统安全漏洞检测技术第三方检测机构

安全测试报告 建立一个安全的Web系统一直是很多企业的目标&#xff0c;一个比较实用的方法就是建立比较容易实现的相对安全的系统&#xff0c;同时按照一定的安全策略建立相应的安全辅助系统&#xff0c;系统安全漏洞检测就是这样一类安全辅助系统。 系统安全漏洞检测技术 1、…
阅读更多...
Kali Linux基础篇(一) 信息收集

Kali Linux基础篇(一) 信息收集

一、前言 1、信息收集分主动信息收集和被动信息收集 主动方式&#xff1a;攻击者直接访问网站&#xff0c;对网站做出扫描、探测等行为&#xff0c;目标系统可能会记录操作信息被动方式&#xff1a;利用第三方的服务访问目标&#xff0c;被动信息收集不会留下访问痕迹&#x…
阅读更多...
华三路由交换技术基础——计算机网络基础

华三路由交换技术基础——计算机网络基础

计算机网络&#xff1a; 定义&#xff1a;一组具有自治权的计算机互联的集合 作用&#xff1a; 1.共享信息资源 2.分解式处理信息 4.负载均衡 5.综合信息服务 它是计算机技术与通信技术的两个领域的结合 一&#xff0c;计算机网络中的基本概念&#xff1a; 局域网&#xff…
阅读更多...
js中如何判断一个变量是否为数字类型？

js中如何判断一个变量是否为数字类型？

聚沙成塔每天进步一点点 ⭐ 专栏简介⭐使用Number.isNaN()方法⭐使用正则表达式⭐使用isNaN()函数⭐ 写在最后 ⭐ 专栏简介 前端入门之旅&#xff1a;探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅&#xff01;这个…
阅读更多...
线性代数的本质(二)——线性变换与矩阵

线性代数的本质(二)——线性变换与矩阵

文章目录 线性变换与矩阵线性变换与二阶方阵常见的线性变换复合变换与矩阵乘法矩阵的定义列空间与基矩阵的秩逆变换与逆矩阵 线性变换与矩阵 线性变换与二阶方阵 本节从二维平面出发学习线性代数。通常选用平面坐标系 O x y Oxy Oxy &#xff0c;基向量为 i , j \mathbf i,…
阅读更多...
【Linux网络编程】Socket-UDP实例

【Linux网络编程】Socket-UDP实例

这份代码利用下面所有知识编写了一个简易聊天室&#xff08;基于Linux操作系统&#xff09;。虽然字数挺多其实并不复杂&#xff0c;这里如果能够看完或许会对你的知识进行一下串联&#xff0c;这篇文章比较杂并且网络编程这块知识需要用到系统编程的知识&#xff0c;希望能帮助…
阅读更多...
内网隧道代理技术（二十四）之 ICMP隧道介绍

内网隧道代理技术（二十四）之 ICMP隧道介绍

ICMP隧道介绍 ICMP介绍 ICMP（InternetControl MessageProtocol）Internet控制报文协议。它是TCP/IP协议簇的一个子协议，用于在IP主机、路由器之间传递控制消息。控制消息是指网络通不通、主机是否可达、路由是否可用等网络本身的消息。这些控制消息虽然并不传输用户数据，但…
阅读更多...
《PostgreSQL与NoSQL：合作与竞争的关系》

《PostgreSQL与NoSQL：合作与竞争的关系》

&#x1f337;&#x1f341; 博主猫头虎&#xff08;&#x1f405;&#x1f43e;&#xff09;带您 Go to New World✨&#x1f341; &#x1f405;&#x1f43e;猫头虎建议程序员必备技术栈一览表&#x1f4d6;&#xff1a; &#x1f6e0;️ 全栈技术 Full Stack: &#x1f4da…
阅读更多...
OpenCV（三十五）：凸包检测

OpenCV（三十五）：凸包检测

1.凸包检测介绍 凸包检测是计算凸包的一种技术&#xff0c;凸包就是&#xff1a;给定二维平面上的点集&#xff0c;将最外层的点连接起来构成的凸边形&#xff0c;它是包含点集中所有的点。 2.凸包检测函数convexHull() void cv::convexHull ( InputArray points, OutputArra…
阅读更多...
华为云云耀云服务器L实例评测｜初始化centos镜像到安装nginx部署前端vue、react项目

华为云云耀云服务器L实例评测｜初始化centos镜像到安装nginx部署前端vue、react项目

文章目录 ⭐前言⭐购买服务器&#x1f496; 选择centos镜像 ⭐在控制台初始化centos镜像&#x1f496;配置登录密码 ⭐在webstorm ssh连接 服务器⭐安装nginx&#x1f496; wget 下载nginx&#x1f496; 解压运行 ⭐添加安全组⭐nginx 配置⭐部署vue&#x1f496; 使用默认的ng…
阅读更多...
PHP8中删除数组中的重复元素-PHP8知识详解

PHP8中删除数组中的重复元素-PHP8知识详解

在 php 8 中&#xff0c;你可以使用array_unique()函数来删除数组中的重复元素。该函数将返回一个新的数组&#xff0c;其中包含原始数组中的唯一元素&#xff0c;而重复的元素只保留第一个出现的。 array_unique()函数返回具有唯一性元素的数组&#xff0c;语法格式如下&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023