排序数组

难度：中等

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

快速排序

算法介绍：
快速排序（英语：Quicksort），又称分区交换排序（partition-exchange sort），简称快排，一种排序算法，最早由东尼·霍尔（Tony Hoare ）提出。在平均状况下，排序 $n$ 个项目要 $O(n\log n)$ 次比较。在最坏状况下则需要 $O(n^2)$ 次比较，但这种状况并不常见。事实上，快速排序 $O(n\log n)$ 通常明显比其他演算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地达成。

快速排序使用分治法（Divide and conquer）策略来把一个序列（list）分为较小和较大的 2 个子序列，然后递归地排序两个子序列。

其基本步骤为：

1. 挑选基准值：从数列中挑出一个元素，称为“基准”（pivot）；
2. 分割（partition）：重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（与基准值相等的数可以到任何一边）。在这个分割结束之后，对基准值的排序就已经完成；
3. 递归排序子序列：递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。

递归到最底部的判断条件是数列的大小是零或一，此时该数列显然已经有序。

思路：
我们定义函数 quicksort(nums, l, r) 为对 nums 数组里 $[l,r]$ 的部分进行排序，如果r-l小于22，则直接进行插入排序。否则每次先调用 partition 函数对 nums 数组里 $[l,r]$ 的部分进行划分，并返回分界值的下标 zoneIndex，然后按上述将的递归调用 quicksort(nums, l, zoneIndex- 1) 和 quicksort(nums, zoneIndex+ 1, r) 即可。

那么核心就是划分函数的实现了，划分函数一开始需要确定一个分界值（我们称之为基准数 pivot)，然后再进行划分。而主元的选取有很多种方式，这里我们采用随机的方式，对当前划分区间 $[l,r]$ 里的数等概率随机一个作为我们的基准数，再将基准数放到区间末尾，进行划分。

整个划分函数 $partition$ 主要涉及分区指示器 $zoneIndex$ ，一开始 zoneIndex = l - 1。
之后依次遍历 $nums[l,r]$的所有元素，只需要做以下两个判断：

1. 如果当前元素小于等于基准数时，首先 $zoneIndex$ 右移一位;
2. 在 $1$ 的基础之上，如果当前元素下标大于 $zoneIndex$ 下标时，当前元素和 $zoneIndex$ 所指元素交换。

样例如下：
注意，分区写法不唯一。该动画并没有随机选取基准数，而是使用第一个数作为基准数，并且没有和最后一个位置置换，所以 $i$ 是从 $l+1$ 开始遍历，最后遍历完毕将 $zoneIndex$ 的位置和 $0$ 的位置进行交换，达到分区效果。

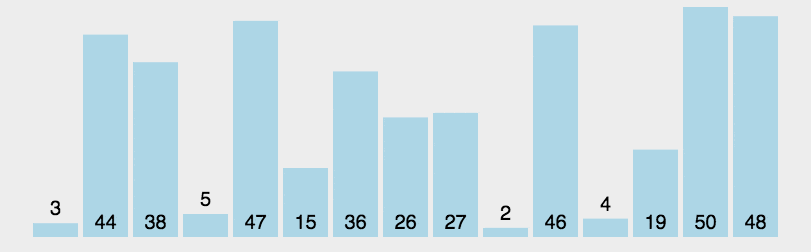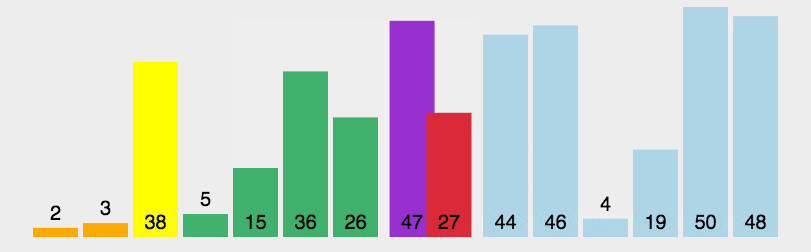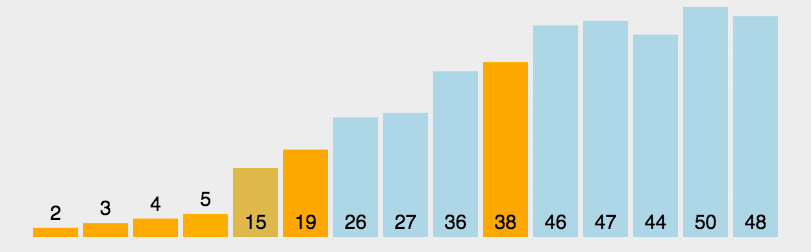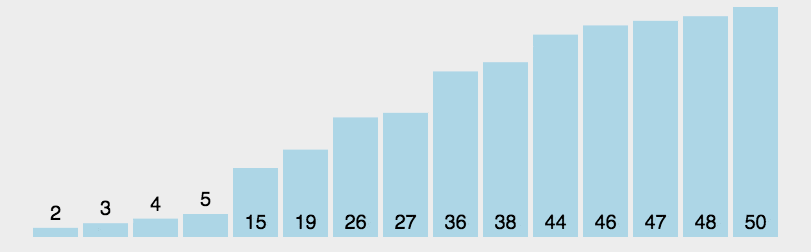
时间复杂度： 基于随机选取主元的快速排序时间复杂度为期望 $O(n\log n)$，其中 $n$ 为数组的长度。

空间复杂度： $O(h)$，其中 $h$ 为快速排序递归调用的层数。我们需要额外的 $O(h)$ 的递归调用的栈空间，由于划分的结果不同导致了快速排序递归调用的层数也会不同，最坏情况下需 $O(n)$ 的空间，最优情况下每次都平衡，此时整个递归树高度为 $\log n$，空间复杂度为 $O(\log n)$。

import random
class Solution:
    # 标准快速排序
    def quicksort(self, nums, l, r):
        # 如果数组长度小于22,则进行插入排序加速,减少递归次数加速排序
        if r - l < 22:
            return self.insertsort(nums, l, r)
        # 获取指示器通过分区后的位置
        zoneIndex = self.partition(nums, l, r)
        # 左右分区分别排序（递归）
        self.quicksort(nums, zoneIndex + 1, r)
        self.quicksort(nums, l, zoneIndex - 1)

    # 快速排序分区
    def partition(self, nums, l, r):
        # 随机选择左右指针中间的一个坐标作为基准数
        pivot = random.randint(l, r)
        nums[pivot], nums[r] = nums[r], nums[pivot]
        # 指示器从 左指针-1 开始
        zoneIndex = l - 1
        # 以下操作的可以节省空间实现原地排序
        for i in range(l, r + 1):
            # 当前元素小于等于基准数
            if nums[i] <= nums[r]:
                # 首先分区指示器进行累加
                zoneIndex += 1
                # 当前元素在分区指示器的右边时，交换当前元素和分区指示器元素
                if zoneIndex < i:
                    nums[zoneIndex], nums[i] = nums[i], nums[zoneIndex]
        return zoneIndex

    # 插入排序
    def insertsort(self, nums, l, r):
        for i in range(l, r + 1):
            index, value = i, nums[i]
            while index > 0 and nums[index-1] > value:
                nums[index] = nums[index-1]
                index -= 1
            nums[index] = value

    def sortArray(self, nums):
        # 为了过最后两个实例...这边就写了标准快排
        if len(set(nums)) == 1:
            return nums
        # 调用快速排序
        self.quicksort(nums, 0, len(nums)-1)
        return nums

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/sort-an-array