（2596. 检查骑士巡视方案leetcode,经典深搜）-------------------Java实现

题目表述

骑士在一张 n x n 的棋盘上巡视。在有效的巡视方案中，骑士会从棋盘的左上角出发，并且访问棋盘上的每个格子恰好一次。

给你一个 n x n 的整数矩阵 grid ，由范围 [0, n * n - 1] 内的不同整数组成，其中 grid[row][col] 表示单元格 (row, col) 是骑士访问的第 grid[row][col] 个单元格。骑士的行动是从下标 0 开始的。

如果 grid 表示了骑士的有效巡视方案，返回 true；否则返回 false。

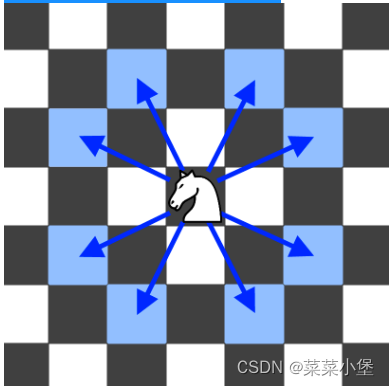
注意，骑士行动时可以垂直移动两个格子且水平移动一个格子，或水平移动两个格子且垂直移动一个格子。下图展示了骑士从某个格子出发可能的八种行动路线。

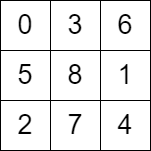
样例

在这里插入图片描述

条件

n == grid.length == grid[i].length
3 <= n <= 7
0 <= grid[row][col] < n * n
grid 中的所有整数互不相同

思路

注意点

ac代码

Java:

package leetcode2596;

import java.util.Scanner;

class Solution {
    public boolean checkValidGrid(int[][] grid) {
        int now = 0;
        int now_x = 0,now_y = 0;
        int n = grid.length;
        boolean flag =false;
        int[][] next_step = new int[][]{{2,1},{2,-1},{-2,1},{-2,-1},
                                        {1,2},{1,-2},{-1,2},{-1,-2}
        };
        if(grid[0][0]!=0)
            return false;
        while(now<n*n){
            for (int i=0;i<8;i++)
            {
                now_x+=next_step[i][0];
                now_y+=next_step[i][1];
                if (now_x>=0&&now_x<n&&now_y>=0&&now_y<n&&grid[now_x][now_y]==(now+1))
                {now++;flag=true;break;}
                now_x-=next_step[i][0];
                now_y-=next_step[i][1];
            }
            if (flag)
                flag=false;
            else
                break;
        }
        System.out.println("now:"+now);
        return now==(n*n-1)?true:false;
    }
}
public class leetcode2596 {
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int n = cin.nextInt();
        cin.nextLine();
        int [][] grid = new int[n][];
        for (int i=0;i<n;i++)
        {
            grid[i] = new int[n];
            for (int j=0;j<n;j++)
                grid[i][j] = cin.nextInt();
            cin.nextLine();
        }

        for (int[] x :grid)
        {
         for (int y:x)
             System.out.print(y+" ");
            System.out.println();
        }
            Solution s = new Solution();
        System.out.println(s.checkValidGrid(grid));
    }
}
//input
//5
//0 11 16 5 20
//17 4 19 10 15
//12 1 8 21 6
//3 18 23 14 9