返回图像处理总目录:《JavaCV图像处理合集总目录》
前言
在DNG格式发布之前,我们先了解一下之前单反相机、苹果和安卓移动端相机拍照输出未经处理的原始图像格式是什么?
RAW
什么是RAW?
RAW是未经处理、也未经压缩的格式。可以把RAW概念化为“原始图像编码数据”或更形象的称为“数字底片”。
RAW是CMOS或者CCD图像感应器将捕捉到的光源信号转化为数字信号的原始数据。
也即RAW文件是一种记录了数码相机传感器的原始信息,同时记录了由相机拍摄所产生的一些元数据(Metadata,如ISO的设置、快门速度、光圈值、白平衡等)的文件。
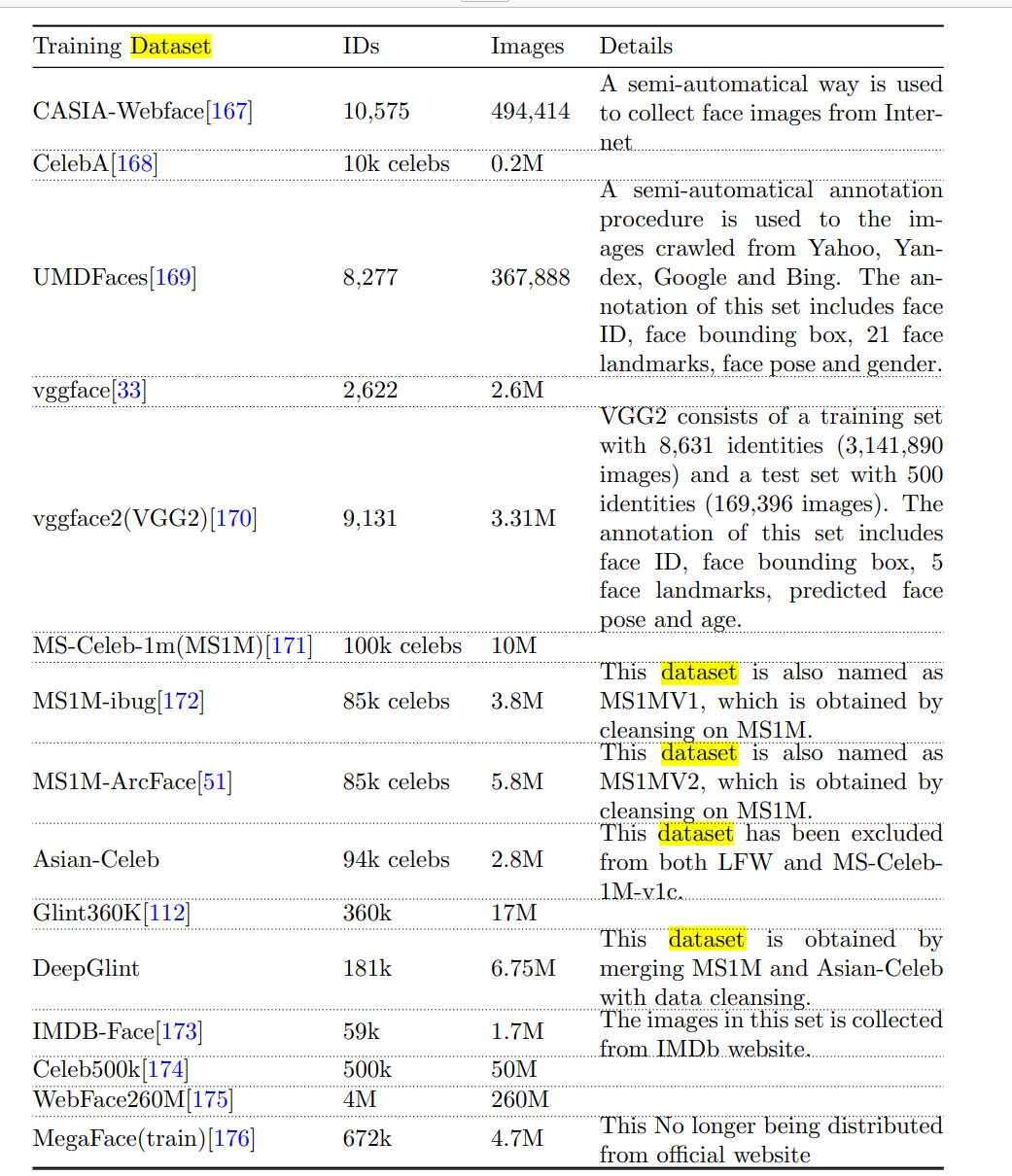
sensor的每一像素对应一个彩色滤光片,滤光片按Bayer pattern分布。将每一个像素的数据直接输出,即RAW RGB data。
Raw data(Raw RGB)经过彩色插值就变成RGB,如下图所示:
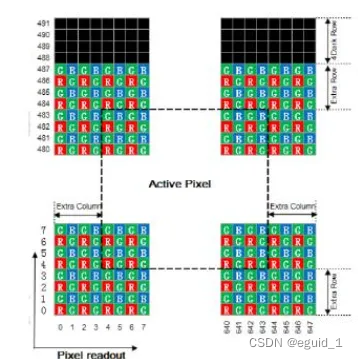
RAW数据是怎么产生的?
通过单反相机、苹果和安卓移动端摄像头,所拍摄的景物通过镜头,投射到传感器上生成光学图像,传感器将光学图像转换成了电信号,电信号再经过模数转换变为数字信号,存储数字信号的文件也就是RAW文件。
RAW与jpeg之类有什么不同?
RAW数据是直接存的未经处理的数字信号。
而jpeg之类的图片格式则是已经经过ISP修饰优化处理过后并且又经过有损压缩过后的数据。

为何要放弃RAW,DNG的由来
因为RAW数据标准不统一
RAW是未经过加工过的档案,原始图档仅是将传感器上所有参数都会记录下来,包括原始曝光、曝光、白平衡、色调、颜色、风格等等数据。
问题就在于每个相机和手机厂商都有自己的RAW格式进行私有化定制,所以导致并没有统一的规范和标准去定义RAW,每家相机和手机厂商都需要有专门的软件来查看和编辑自家的RAW格式。
DNG标准早在2015年就已经发布了,最新的DNG 1.7.0.0标准规范是Adobe公司在2023年6月发布。
目前所有单反相机、苹果、华为、小米、一加等手机厂商都已经支持DNG格式输出拍照原始图像数据(DNG)。
DNG想要统一原始数据标准
数字负片 (DNG)
是一种公共存档格式,可用于存储由各种数字相机生成的原始数据文件。对于通过各种相机型号创建的原始数据文件,一直欠缺一种适用的开放标准,而数字负片解决了这一问题,可确保摄影师能够轻松地访问他们的文件。
除“数字负片规范”外,Adobe 还提供了免费的 Adobe DNG Converter。这里不提供下载软件地址,如果有兴趣可以自行到官网下载。

支持的相机尝试列表:https://helpx.adobe.com/cn/camera-raw/using/supported-cameras.html
由于DNG格式比较新,目前支持DNG格式的软件不多,基本只有Adobe自家的软件才能支持:Photoshop、Photoshop Elements、Lightroom 和 Lightroom Classic等。
FFmpeg目前还不能支持DNG格式,但是由于DNG与TIFF的特殊关系,可以通过将DNG改后缀为TIFF来用ffmpeg打开。因此对于开发者来说,暂时开发量有点大,因为规范推出的时间太短,开源库估计还要再等等才有。
TIFF, TIFF/EP, DNG, RAW之间的关系
TIFF和DNG同为Specification,分别定义了后缀名为.tif/.tiff和.dng的文件格式同时在TIFF Specification也定义个baseline及部分扩展的tag。
TIFF/EP则定义并规范了在电子影像中所使用的TAG。
DNG同时与TIFF和TIFF/EP兼容,并包含了EXIF和XMP信息。DNG实际上就是扩张的TIFF, 把DNG的扩展名改成TIF就可以直接预览图片。
DNG格式标准规范
下载地址:https://download.csdn.net/download/eguid_1/88335365
返回图像处理总目录:《JavaCV图像处理合集总目录》