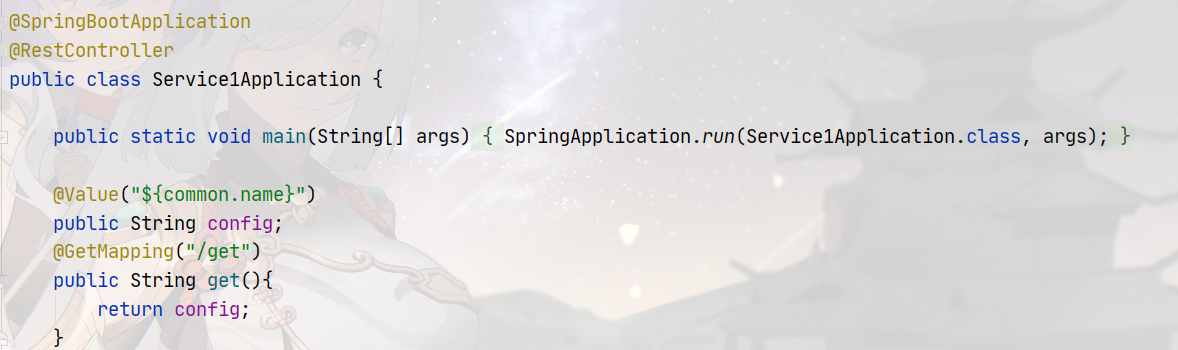
题目描述

思路讲解

这道题的数据量是10^6，直接用floyd算法，肯定是不行的

此处介绍新的思路：多源BFS

我们的核心目的是，对于每一个终点（即此处的顾客）能够找到离它最近的源点（即此处的餐馆）

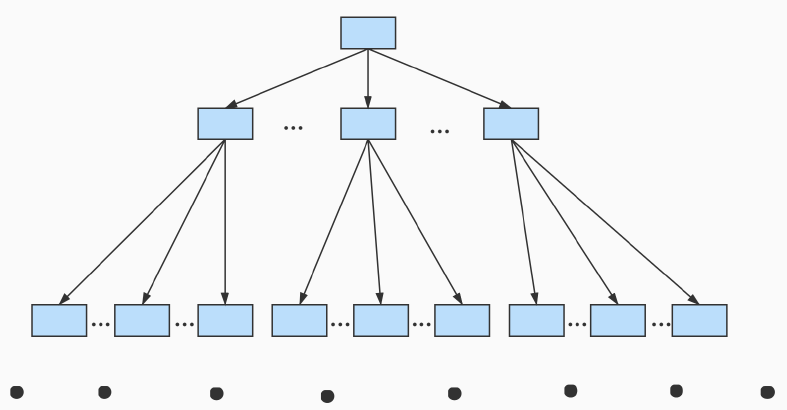
思路如下，我们假想一个“超级源点”S，如图所示：

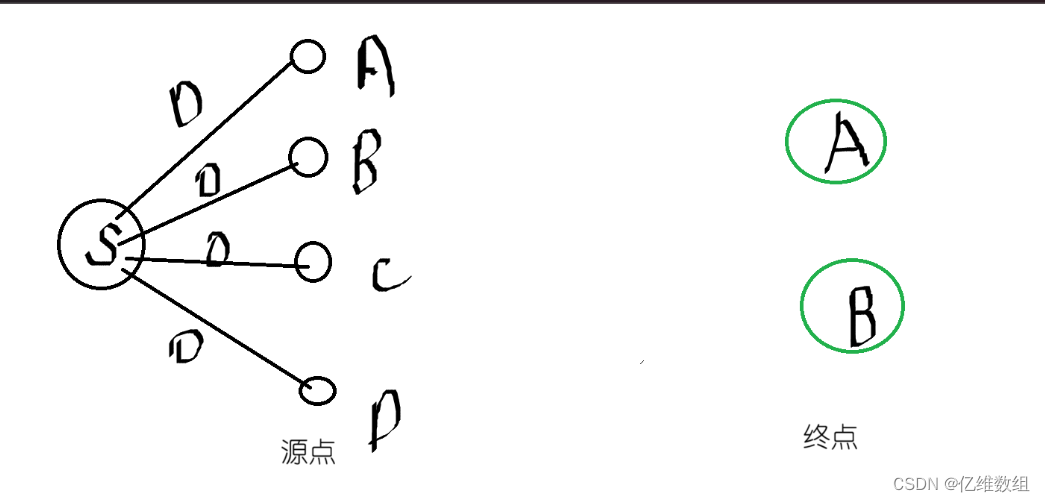
这个超级遇到源点距离每一个源点为0

那么算某个终点（比如A）到源点A,B,C,D的最短距离，就可以转换为求A到S的距离

代码应该怎么实现呢？

很简单，假设提前已经把S入队了，直接进入下一步：S出队，然后入队源点A,B,C,D即可

其它和普通BFS一毛一样

时间复杂度：O（N）

最后注意，答案可能爆int，所以用longlong

满分代码

#include<iostream>
#include<queue>
#include<utility>
#include<cstring>
using namespace std;
const int N=1010;
typedef long long LL;
typedef pair<int,int>PII;
queue<PII>q;
int n,m,d,k;
int dist[N][N];
struct Target{
	int x,y,c;
}target[N*N];
LL res=0;
bool trap[N][N];
void bfs()
{
	int dx[]={-1,0,1,0},dy[]={0,1,0,-1};
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		for(int i=0;i<4;i++)
		{
			int a=t.first+dx[i],b=t.second+dy[i];
			if(a<1||a>n||b<1||b>n||trap[a][b])continue;
			if(dist[a][b]>dist[t.first][t.second]+1)
			{
				dist[a][b]=dist[t.first][t.second]+1;
				q.push({a,b});
			}
		}
	}
}
int main()
{
	scanf("%d%d%d%d",&n,&m,&k,&d);
	memset(dist,0x3f,sizeof dist);
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		q.push({x,y});
		dist[x][y]=0;
	}
	for(int i=1;i<=k;i++)
	{
		int x,y,c;
		scanf("%d%d%d",&x,&y,&c);
		target[i].x=x,target[i].y=y,target[i].c=c;
	}
	for(int i=1;i<=d;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		trap[x][y]=true;
	}
	bfs();
	for(int i=1;i<=k;i++)
	res+=(LL)dist[target[i].x][target[i].y]*target[i].c;
	cout<<res;
	return 0;
}