系列文章目录
提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加
例如:第一章 Python 机器学习入门之pandas的使用
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 系列文章目录
- 前言
- 一、二分查找
- 1、思路
- 2、初步代码复现
- 3、整数溢出的情况
- 如图:中间索引上的值 + 右边界索引上的值 会造成`整数溢出`:
- 4、解决:使用位运算符 >>>
- 二、冒泡排序
- 1、思路
- 2、初步实现
- 比较次数逐次递减
- 问题:在第7轮冒泡时,数组已经排序完成,不需要后续继续循环
- 3、优化1:外轮循环
- `设置一个boolean类型,当不再冒泡时break跳出`
- 结果:
- 问题:内循环的比较次数还有优化空间
- 4、优化2:内轮循环
- `内轮循环比较时记录最后比较的下标,在下一外轮时从下标数开始`
- 结果:
- 三、选择排序
- 1、思路
- 2、实现
- 结果:
- 优点:把每轮内循环的交换,放到了外循环中进行,所以和冒泡相比的每轮内循环都可能进行交换,`选择排序的交换次数大幅度减少`
- 3、与冒泡排序的比较
- a、第三点的集合有序度高,冒泡优于选择。指的是:
- b、稳定排序和不稳定排序,是指排序时是否打乱原来相同元素的位置
- 四、插入排序
- 1、思路
- 2、初步实现
- 结果:插排
- 3、与选择排序比较
- 在这里插入图片描述
- 五、希尔排序(了解)
- 1、提出原因
- 2、希尔排序是插入排序的优化
- `能够快速的将大数移动到数组后半部分`
- 链接: [希尔排序](https://blog.csdn.net/m0_63033419/article/details/127524644?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169457506116800188536874%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169457506116800188536874&biz_id=0&utm_medium=distribute.pc_chrome_plugin_search_result.none-task-blog-2~all~top_positive~default-2-127524644-null-null.nonecase&utm_term=%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F&spm=1018.2226.3001.4187)
- 七、待更新。。。
前言
后续可能用到的 swap() 交换方法
//交换
public static void swap(int a[], int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
提示:以下是本篇文章正文内容,下面案例可供参考
一、二分查找
1、思路

2、初步代码复现
@Test
public void test01() {
int[] arr = {1, 2, 3, 5, 7, 8, 9, 12, 23, 34, 45, 56, 67, 90};
int target = 67;
int i = binarySerch(arr, target);
if (i != -1) {
System.out.println("找到了,在第" + i + "位");
} else System.out.println("未找到!");
}
//二分查找
public static int binarySerch(int[] a, int t) {
int l = 0;
int r = a.length - 1;
int m;
while (l <= r) {
m = (l + r) / 2;//如果遇到整数溢出问题 需要解决
// m = (l + r) >>> 1;//使用无符号右移的方式 效率更高 而且不会溢出
if (a[m] == t) {
return m;
} else if (a[m] > t) {//要查找的值比中间值小,去左边找 将右边界点设置成a[m-1]
r = m - 1;
} else if (a[m] < t) {//要查找的值比中间值大,去右边找 将左边界点设置成a[m+1]
l = m + 1;
}
}
return -1;
}
执行
3、整数溢出的情况
如果数组长度超过了int的最大存储空间

如图:中间索引上的值 + 右边界索引上的值 会造成整数溢出:
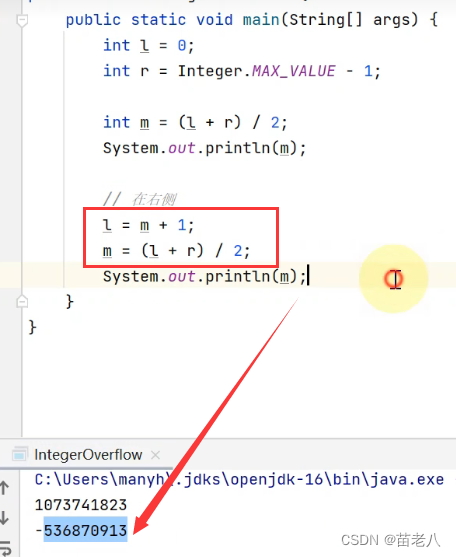
4、解决:使用位运算符 >>>

二、冒泡排序
1、思路

2、初步实现
//冒泡
@Test
public void test02() {
int a[] = {0, 1, 67, 456, 3, 23, 64, 63, 75, 767, 123, 12828, 25236};
// int a[] = {1,2,3,4,5,6,7,8,9,10};
bubble(a);
}
public static void bubble(int a[]) {
for (int i = 0; i < a.length - 1; i++) {
for (int j = 0; j < a.length - 1 - i; j++) {//冒出的泡 所以需要-i
System.out.println("比较次数:" + j);
if (a[j] > a[j + 1]) {
swap(a, j, j + 1);
}
}
System.out.println("第" + i + "轮冒泡排序:" + Arrays.toString(a));
}
}
比较次数逐次递减

问题:在第7轮冒泡时,数组已经排序完成,不需要后续继续循环
3、优化1:外轮循环
设置一个boolean类型,当不再冒泡时break跳出
//冒泡优化一 没有比较就跳出
public static void bubble(int a[]) {
for (int i = 0; i < a.length - 1; i++) {
boolean swapped = false;//省去多余的冒泡,因为有些数组原本就是有序的
for (int j = 0; j < a.length - 1 - i; j++) {
System.out.println("比较次数:" + j);
if (a[j] > a[j + 1]) {
swap(a, j, j + 1);
swapped = true;//发生了交换
}
}
System.out.println("第" + i + "轮冒泡排序:" + Arrays.toString(a));
if (!swapped) {//如果没有发生交换,则进行break跳出
break;
}
}
}
结果:
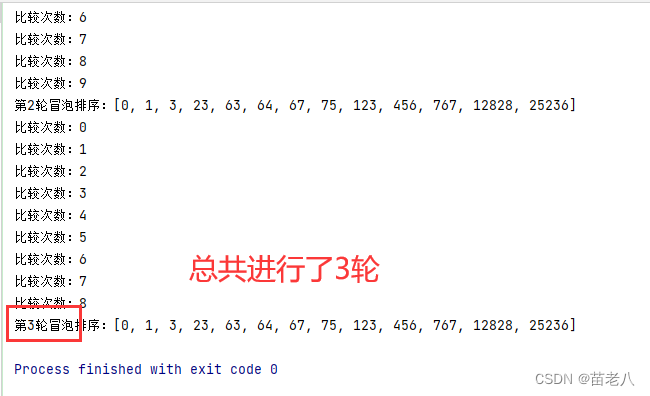
问题:内循环的比较次数还有优化空间

4、优化2:内轮循环
内轮循环比较时记录最后比较的下标,在下一外轮时从下标数开始
//冒泡优化2 原数组中大数在后时,可以跳过当次冒泡
//所以记录最后一次冒泡的下标位置 下一次冒泡即可按下标位置作为冒泡次数
public static void bubble2(int a[]) {
int length = a.length - 1;
int s = 0;//记录交换轮数,可不用
while (true) {
int last = 0;//表示最后一次交换索引位置
for (int j = 0; j < length; j++) {
System.out.println("比较次数:" + j);
if (a[j] > a[j + 1]) {
swap(a, j, j + 1);
last = j;
}
}
length = last;
System.out.println("第"+(s++)+"轮冒泡排序:" + Arrays.toString(a));
if (length == 0) {//当最后一次比较的下标为0时 结束
break;
}
}
}
结果:
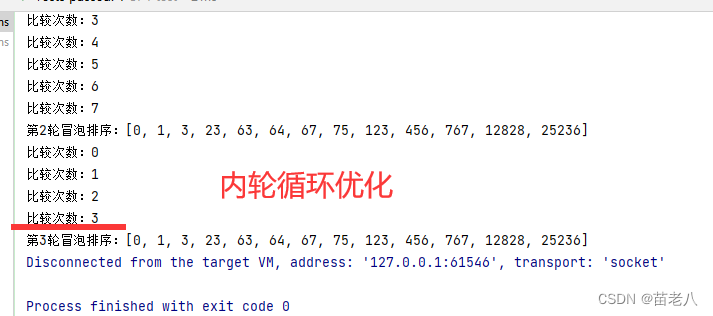
三、选择排序
1、思路

2、实现
@Test
public void test03() {
//选择排序
int a[] = {1, 45, 12, 34, 42, 14, 31, 76, 58, 94};
select(a);
}
//选择排序
public static void select(int[] a) {
//i 代表每轮选择最小的元素要替换的位置下标索引
for (int i = 0; i < a.length; i++) {
int s = i;//代表最小的元素
for (int j = s + 1; j < a.length; j++) {//需要比较的下一位
if (a[j] < a[s]) {
s = j;
}
}
if (s!=i) {//当每轮最开始比较的数是当轮最小值时,不交换,减少交换次数
swap(a, i, s);
}
System.out.println("第" + i + "次排序后:" + Arrays.toString(a));
}
}
结果:

优点:把每轮内循环的交换,放到了外循环中进行,所以和冒泡相比的每轮内循环都可能进行交换,选择排序的交换次数大幅度减少
3、与冒泡排序的比较

a、第三点的集合有序度高,冒泡优于选择。指的是:
选择:
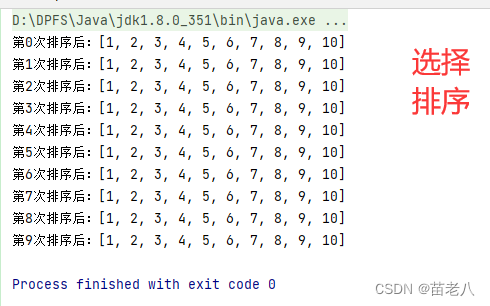
冒泡:

b、稳定排序和不稳定排序,是指排序时是否打乱原来相同元素的位置
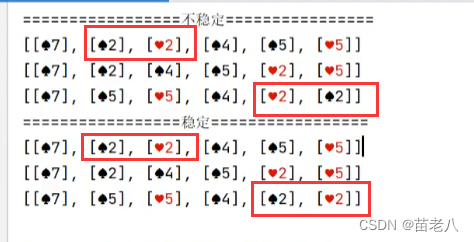
四、插入排序
1、思路

2、初步实现
@Test
public void test04() {
//插入排序
int a[] = {1, 45, 12, 34, 42, 14, 31, 76, 58, 94};
// int a[] = {1,2,3,4,5,6,7,8,9,10};
insert(a);
}
private void insert(int[] a) {
// i 代表待插入元素的索引
for (int i = 1; i < a.length; i++) {
int t = a[i];//代表待插入元素的值
int j = i - 1;//代表左侧已排序的索引下标
while (j >= 0){
if (t < a[j]) {
a[j+1] = a[j];
}else break;//因为左边默认是排好序的,所以不再进行比较
j--;//确保每比较一个就往左更新下标 直到为0或者已排序区域的值都比待插入的值小
}
a[j+1] = t;
System.out.println(Arrays.toString(a));
}
}
结果:插排

3、与选择排序比较
五、希尔排序(了解)
1、提出原因
使用插入排序时,如果数组前半部分有多个大数,且数组长度很长时,插排会将大数移动到数组后半部分,此时移动次数会大大增加,所以提出了希尔排序
2、希尔排序是插入排序的优化
将原本插排中相邻间隔为1的两个数进行比较 优化成相邻间隔为n的两个数进行比较,n可根据长度调整
如n为5
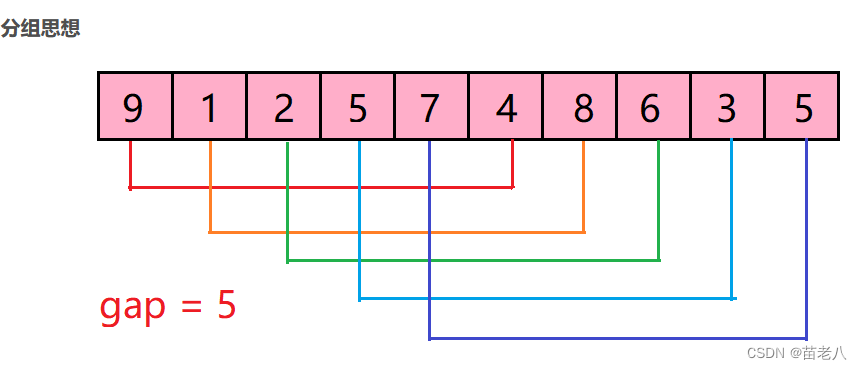








![docker 镜像内执行命令显示:You requested GPUs: [0] But your machine only has: []](https://img-blog.csdnimg.cn/5de3a7e45a6d4cbab54af11bfb901861.png)