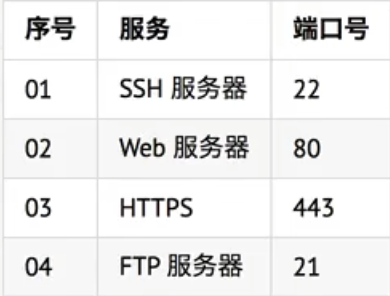
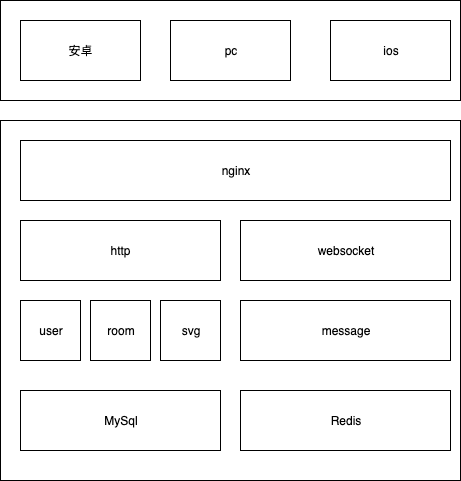
Problem Description

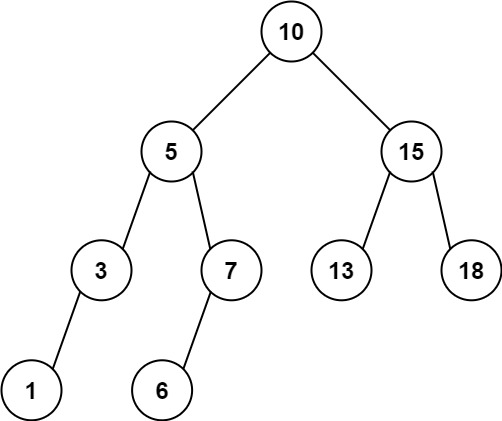
平衡二叉树又称AVL树，它是一种具有平衡因子的特殊二叉排序树。平衡二叉树或者是一棵空树，或者是具有以下几条性质的二叉树：

1.       若它的左子树不空，则左子树上所有结点的值均小于它的根节点的值；

2.       若它的右子树不空，则右子树上所有结点的值均大于它的根节点的值；

3.       它的左右子树也分别为平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

若将二叉树上结点的平衡因子定义为该结点的左子树深度减去它的右子树的深度，则平衡二叉树上的所有结点的平衡因子只可能为-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1，则这棵二叉树就是不平衡的。

通过平衡二叉树的性质不难得知，其插入、删除、查询都操作的时间复杂度均为O(log2n)。

维持平衡二叉树性质的操作可以被称为旋转。其中平衡二叉树的右旋处理可以描述如下：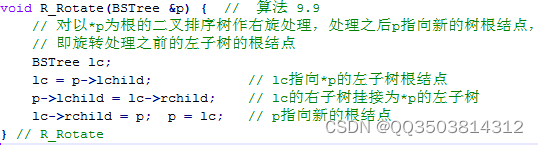

 而其左旋处理与右旋正好相反，可以描述如下：

 在本题中，读入一串整数，首先利用这些整数构造一棵平衡二叉树。另外给定多次查询，利用构造出的平衡二叉树，判断每一次查询是否成功。

 

 Input Description

 

输入的第一行包含2个正整数n和k，分别表示共有n个整数和k次查询。其中n不超过500，k同样不超过500。

第二行包含n个用空格隔开的正整数，表示n个整数。

第三行包含k个用空格隔开的正整数，表示k次查询的目标。

 

 Output Description

 

只有1行，包含k个整数，分别表示每一次的查询结果。如果在查询中找到了对应的整数，则输出1，否则输出0。

请在每个整数后输出一个空格，并请注意行尾输出换行。

Sample Input

8 3
1 3 5 7 8 9 10 15
9 2 5

 Sample Output

1 0 1 

 Hint

在本题中，首先需要按照题目描述中的算法完成平衡二叉树的构造过程，之后需要通过在平衡二叉树中的不断向下查找，将需要查询的值与当前节点的值进行比较，直到确定被查询的值是否存在。

通过课本中的性能分析部分，不难发现平衡二叉树的查找、插入、删除等操作的时间复杂度均为O(log2n)，这是通过利用旋转操作使二叉树保持平衡状态而保证的。

 我的想法：

 我的代码：

#include <iostream>
#include <stdio.h>
#include <algorithm>
using namespace std;

typedef struct Node
{
	int v, height;
	Node * lchild, *rchild;
}Node, *TNode;

int GetHeight(TNode &Tree)//获取当前节点的高度
{
	if (Tree == NULL)
	{
		return 0;
	}
	return Tree->height;
}

void UpdateHeight(TNode &Tree)
{
	Tree->height = max(GetHeight(Tree->lchild), GetHeight(Tree->rchild)) + 1;
	//树高为左右子树中的最大值加一
}

int GetTreeHeight(TNode &Tree)//获取左右节点高度差
{
	return GetHeight(Tree->lchild) - GetHeight(Tree->rchild);
}

void L(TNode &Tree)//左旋
{
	TNode temp = Tree->rchild;//记录Tree的右孩子
	Tree->rchild = temp->lchild;//改变树的右孩子为树右孩子的右孩子
	temp->lchild = Tree;///
	UpdateHeight(Tree);
	UpdateHeight(temp);
	Tree = temp;
}

void R(TNode &Tree)//右旋
{
	TNode temp = Tree->lchild;
	Tree->lchild = temp->rchild;
	temp->rchild = Tree;
	UpdateHeight(Tree);
	UpdateHeight(Tree);
	Tree = temp;
}

void Inster(TNode &Tree, int e)
{
	if (Tree == NULL)
	{
		TNode temp = new Node;               //创建一个新的节点，并用temp指向这个节点
		temp->v = e;                         //赋予该树权值
		temp->lchild = temp->rchild = NULL;  //左右孩子置为空
		temp->height = 1;                    //树高为1
		Tree = temp;
		return;
	}
	if (e < Tree->v)//要擦入的元素小于根元素
	{
		Inster(Tree->lchild, e); //看左孩子
		UpdateHeight(Tree);      //更新一下树高
		if (GetTreeHeight(Tree) == 2)//左右子树树高相差为2
		{
			if (GetTreeHeight(Tree->lchild) == 1)//右子树的左右孩子树高相差为1
			{
				R(Tree);
			}
			else if(GetTreeHeight(Tree->lchild) == -1)
			{
				L(Tree->lchild);
				R(Tree);
			}

		}
	}
	else if(e > Tree->v)//大于要插入的元素
	{
		Inster(Tree->rchild, e);//看右孩子
		UpdateHeight(Tree);//再次更新树高
		if (GetTreeHeight(Tree) == -2)
		{
			if (GetTreeHeight(Tree->rchild) == -1)//RR型
			{
				L(Tree);
			}
			else if(GetTreeHeight(Tree->rchild) == 1)//RL型
			{
				R(Tree->rchild);
				L(Tree);
			}
		}
	}
}


TNode CreateTree(int n)
{
	int e = 0;
	TNode Tree = NULL;

	//初始化树
	for (int i = 0; i < n; i++)
	{
		cin >> e;
		Inster(Tree, e);
	}
	return Tree;
}

int Search(TNode &Tree, int e)
{
	if (Tree == NULL)
	{
		return 0;
	}
	else if (Tree->v == e)
	{
		return 1;
	}
	else if (Tree->v < e)
	{
		Search(Tree->rchild, e);
	}
	else
	{
		Search(Tree->lchild, e);
	}
}

int main()
{
	int n, k;
	cin >> n >> k;//n表示有n个整数，k表示有k个操作

	//先来构建二叉树
	TNode root = CreateTree(n);

	int ch;//ch是要匹配的数
	while (k--)
	{
		cin >> ch;//匹配成功输出1，失败输出0
		printf("%d ", Search(root, ch));
	}
	printf("\n");
	return 0;
}