1 时钟Clock

理想的时钟模型是一个占空比为50%且周期固定的方波。时钟是FPGA中同步电路逻辑运行的一个基准。理想的时钟信号如下图:

2 时钟抖动Clock Jitter

理想的时钟信号是完美的方波，但是实际的方波是存在一些时钟抖动的。那么什么是时钟抖动呢?时钟抖动，Clock Jitter，是相对于理想时钟沿，实际时钟存在不随时间积累的、时而超前、时而滞后的偏移称为时钟抖动（时钟脉冲宽度发生暂时变化，也就是T cycle【时钟周期】或大或小)。有抖动的时钟信号如下图: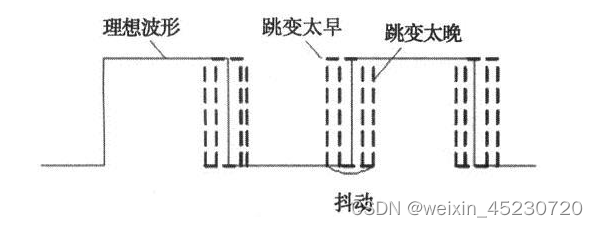

3 时钟偏差Clock Skew

        时钟偏差，Clock Skew，是指同一个时钟域内的时钟信号到达数字电路各寄存器所用时间的差异。时序分析的起点一般是源寄存器(reg1) ，终点—般是目标寄存器(reg2)。
        时钟信号也会走线，那么和其它信号的传输一样，就会有延时。下图中，时钟信号从时钟源传输到源寄存器的延时我们定义为Tc2s，传输到目标寄存器的延时我们定义为Tc2d。如下图:

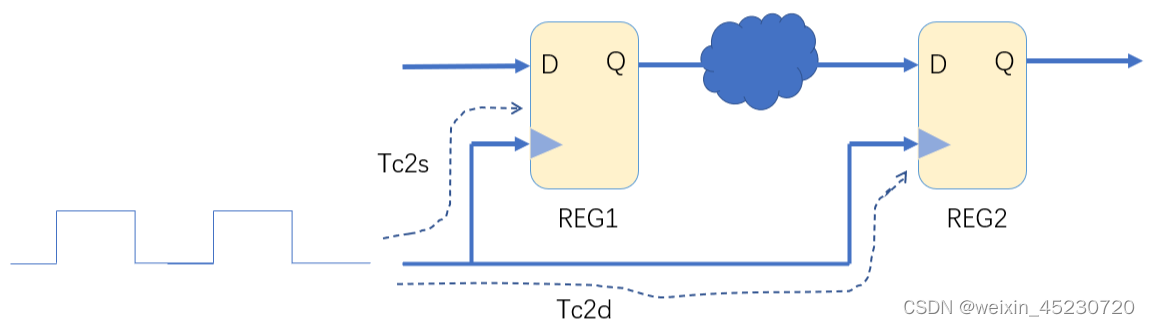
时钟网络延时 Tskew就是Tc2d与Tc2s之差，即Tskew=Tc2d - Tc2s。如下图: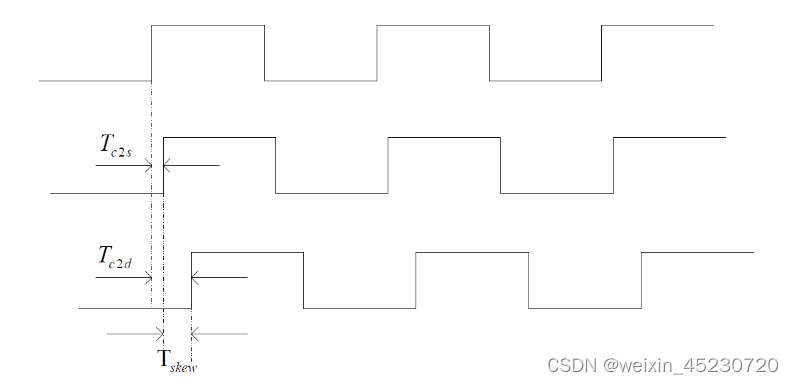

第一个方波是时钟源，第二个方波为时钟到达REG1时的波形，第三个方波为时钟到达REG2时的波形，从图上可以看出Tskew是时钟到达两个寄存器时的相位偏差。
 

4 时钟不确定性Clock Uncertainty

Clock Uncertainty，即时钟的不确定性。时钟的不确定性主要是由Clock Skew和.Jitter构成。因此Clock Uncertainty = ClockSkew + Clock Jitter。大家搞明白什么是Skew和Jitter，那么也就明白什么是Clock Uncertainty。
一般标准的时序约束文件中，都需要加Clock Uncertainty的约束，这个约束是为了让时序分析更贴近真实的电路设计。对于Uncertainty的设置，每种工艺，或者每种设计来说，都不尽相同。

5 同步电路和异步电路

简单来讲，FPGA设计中寄存器全部使用一个时钟的设计是同步设计电路，FPGA设计寄存器使用多个时钟的设计是异步设计电路。我们说的所有时序分析都是建立在同步电路的基础上的，异步电路不能做时序分析(或者说只能做伪路径约束)。
异步电路由于使用的时钟不同，导致上游寄存器的输出数据进入下游寄存器的时间是任意的，这非常可能导致不满足下游寄存器的建立时间要求和保持时间要求，从而导致亚稳态。同样的原因，由于两者时钟不同，所以也不法建立对应的模型来分析异步电路是否能满足时序要求。

6 建立时间(Setup Time）和保持时间(Hold Time)

建立时间和保持时间是寄存器的固定属性，为了使寄存器稳定地采样到当前D端的数据，D端数据必须满足建立时间和保持时间的要求:
建立时间: Setup Time，缩写是TSu，即在时钟上升沿之前数据必须稳定的最短时间。

保持时间: Hold Time，缩写是 Th，即在时钟上升沿之后数据必须稳定的最短时间

通俗来讲:建立时间和保持时间就是在寄存器采样窗口中输入数据必须保持不变，以免寄存器无法稳定采样。也就是说，在我寄存器的采样窗口之前你输入数据就必须要保持稳定，即输入数据不能来的太晚（建立时间);同样的，你寄存器的输入数据也必须在我寄存器的采样窗口结束后才变化，在此之前必须保持问题，即输入数据不能走的太早（保持时间)。
建立时间和保持时间的示意图如下:

7  什么是时序分析?

时序分析主要有两种办法:

        静态时序分析: (static timing analysis，STA)，是遍历电路存在的所有时序路径，根据给定工作条件(PVT)下的时序库.lib文件计算信号在这些路径上的传播延时，检查信号的建立和保持时间是否满足约束要求，根据最大路径延时和最小路径延时找出违背时序约束的错误。
        动态时序分析: (dynamic timing analysis，DTA)，通常是所有的输入信号都会给一个不同时刻的激励，在testbech ( sp或者.v)中设置一段仿真时间，最后对仿真结果进行时序和功能分析。这里的仿真可以是门级或者晶体管级，包括spice格式和RTL格式的网表。
        STA不需要输入向量就能穷尽所有的路径，运行速度快，占用内存小。不仅可以对芯片设计进行全面的时序功能检查，还可以利用时序分析的结果来优化设计。DTA的优点是结果精确，并且适用于更多的设计类型;缺点是速度慢，并且可能会遗漏一些关键路径。一般来讲，我们提到的时序分析都是指静态时序分析STA。

8  什么是时序约束?

        了解了时序分析后，其实时序约束也就好理解了。简单来讲，时序约束就是你要告诉综合工具，你的标准是什么。综合工具应该如何根据你的标准来布线，以满足所有寄存器的时序要求。
        在FPGA设计中，一旦时钟频率上升，那么时钟周期就会减少。不难想象频率越高，时钟周期越小，而建立时间和保持时间的要求不变，那么对应的，满足建立时间和保持时间也会变难，因为留给信号到达的窗口变小了嘛!
        但是综合工具怎么知道你的设计要求是多少?那它又怎么去约束时钟呢?所以我们开发者需要告诉综合工具，我们的约束标准是什么，综合工具才可以根据这个标准去布局布线，从而满足我们的时序要求。
        假设信号需要从输入到输出在FPGA内部经过一些逻辑延时和路径延时。我们的系统要求这个信号在FPGA内部的延时不能超过13ns(约束条件)，而开发工具在执行过程中找到了下图所示的一些可能的布局布线方式。图中区域1的延迟是5ns，区域2的延迟是7ns，区域3的延迟是5ns，区域4的延迟是11ns。那么，怎样的布局布线能够达到我们的要求呢?仔细分析一番，发现所有路径的延时可能为12ns(走路径1)、16ns(走路径3)、21ns(走路径2到路径5)、17ns(走路径2到路径4)，只有1条路径能够满足要求，布局布线工具就会选择满足要求的路径1。

        这个地方我们系统要求这个信号在FPGA内部的延时不能超过13ns，是有1条路径可以满足要求的，那么如果系统要求这个信号在FPGA内部的延时不能超过5ns，那么没有任何一条路径可以满足要求，这个就说明这个FPGA器件速度等级比较慢，可以选择速度等级比较快的FPGA器件，当然也有可能是系统要求过于苛刻(过约束)。
        如果系统要求这个信号在FPGA内部的延时不能超过18ns，那么是有3条路径可以满足要求的，分别是走路径1，走路径3，走路径2到路径4这3条路径，这个说明如果系统要求松，那么布局布线工具可以选择就很多，这样对布局布线工具比较友好。时序分析的前提就是我们先提出要求，然后时序分析工具才会根据特定的时序模型进行分析，即有约束才会有分析。如果我们不添加时序约束，那么时序分析工具就不会去分析时序和做时序收敛。也就是说，只有在对设计添加了时序约束后，系统的时序问题才有可能暴露出来.

9  什么是时序收敛?

        在我们给出时序约束的标准后，综合工具会自动进行时序分析，然后出具时序报告表。如果我们的设计欠佳或者约束条件过高，导致综合工具无法实现满足我们要求的布局布线。这种情况下，就可以说该设计是不满足时序要求的。
通过修改RTL设计(如减少扇出、重新布线优化、重定时、流水线切割等一系列方法)或其他方法，来使综合工具能重新实现满足我们设计要求的布局布线的这一设计过程，就被称为时序收敛Timing closure。同样的，当所有的时序设计要求被满足后，也可以说这一设计是时序收敛的。
        简单点讲，时序收敛就是你改作业的过程，把不及格的作业通过改、抄等手段给改到合格的过程就是时序收敛。
        好的时序是设计出来的，不是约束出来的。好的约束必须以好的设计为前提。没有好的设计，在约束上下再大的功夫也是没有意义的。不过，通过正确的约束也可以检查设计的优劣，通过时序分析报告可以检查出设计上时序考虑不周的地方，从而加以修改。
        通过多次“分析—修改—分析”的迭代也可以达到完善设计的目标。所以说，设计是约束的根本，约束是设计的保证，二者是相辅相成的。

10  组合逻辑与时序逻辑

数字电路根据逻辑功能的不同特点，可以分成两大类:组合逻辑电路与时序逻辑电路。

组合逻辑电路的最大特点是输出是实时跟随输入变化的，如下面的组合逻辑，如果两个输入之间到达的路径延时不一致的话，则很容易产生毛刺。偏偏FPGA又不是理想器件，在资源被大量使用的情况下，要做到不同的路径达到门电路的延时一致几乎是不可能的，所以可以说纯组合逻辑电路的毛刺现象几乎是不可避免的。毛刺的产生很多时候都是个灾难，因为它并不是你预期设计的一部分，这相当于你的设计遇上了没有预料到的输入情况，所以输出在很大程度上也会变得不可控。
 

时序逻辑电路的最大特点是输出不是实时跟随输入变化的，而是在时钟的上升沿(或下降沿，一般以上升沿为主流)统一发生变化(诚然这个变化也不是瞬时的，还需要一定的Tco时间)。在时钟的上升沿之前，只要输入满足建立时间和保持时间的要求，则任你如何有毛刺也不会对输出造成影响，这很容易理解，因为在非上升沿不会发生采样，自然也不会有输出。
 

时序逻辑电路解决了组合逻辑电路无法解决的毛刺问题，将电路的行动全部置于统一的行动之下...钟。在时钟信号的控制下，整个电路可以有条不紊的运行。当然，组合逻辑电路并不是被替代，因为我们仍然需要其实现逻辑功能。所以组合逻辑与时序逻辑可以说是共生，你中有我我中有你----组合逻辑实现逻辑功能，而时序逻辑则将电路的运行置于统一的管理之下。
 

11 同步电路和异步电路

基于FPGA的设计Q几乎都是时序逻辑电路，极少会有设计纯组合逻辑电路的情况。因此，时序逻辑电路在FPGA的设计中占有非常重要的地位。对于时序逻辑，按信号间关系来看，又可分为同步时序逻辑和异步时序逻辑，简称同步逻辑和异步逻辑。

简单来讲，FPGA设计中寄存器全部使用一个时钟的设计是同步设计电路，FPGA设计寄存器使用多个时钟的设计是异步设计电路。我们说的所有时序分析都是建立在同步电路的基础上的，异步电路不能做时序分析(或者说只能做伪路径约束)。
异步电路由于使用的时钟不同，导致上游寄存器的输出数据进入下游寄存器的时间是任意的，这非常可能导致不满足下游寄存器的建立时间要求和保持时间要求，从而导致亚稳态。同样的原因，由于两者时钟不同，所以也不法建立对应的模型来分析异步电路是否能满足时序要求。
所以，对FPGA的时序分析其实主要就是对同步时序逻辑电路进行分析，然后再做约束。那么到底要约束些什么?
 

12 建立时间与保持时间

时序逻辑电路的基础是触发器FF，对FF的使用有两个要求是必须满足的----建立时间与保持时间。
        建立时间: Setup Time，缩写是TSu，即在时钟上升沿之前数据必须稳定的最短时间
        保持时间: Hold Time，缩写是 Th，即在时钟上升沿之后数据必须稳定的最短时间
通俗来讲:建立时间和保持时间就是在寄存器采样窗口中输入数据必须保持不变，以免寄存器无法稳定采样。也就是说，在我寄存器的采样窗口之前你输入数据就必须要保持稳定，即输入数据不能来的太晚(建立时间)﹔同样的，你寄存器的输入数据也必须在我寄存器的采样窗口结束后才变化，在此之前必须保持问题，即输入数据不能走的太早（保持时间)。
建立时间和保持时间的示意图如下:

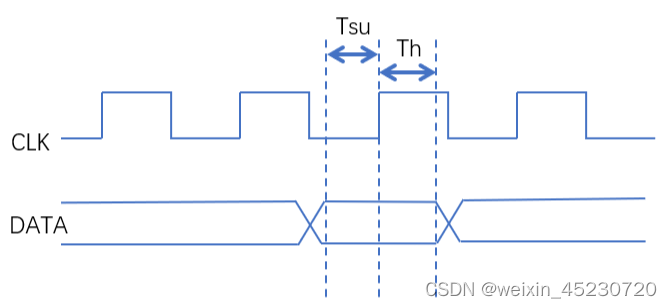
        建立时间和保持时间是触发器的固定属性，也就是说同一FPGA型号其所有的FF的建立时间和保持时间都是相同的，而不同的FPGA型号之间，其建立时间与保持时间则不同。关于FPGA对应的建立时间和保持时间可以通过手册来查询，也可以用vivado做时序分析时查询。高级的FPGA芯片其建立时间和保持时间会比低级的FPGA芯片较小，这也是其能运行频率更高的原因。
        了解FPGA的建立时间和保持时间非常重要，它是我们进行时序分析的基础，甚至可以说，时序分析就是要分析所有的FF是不是都满足建立时间与保持时间的要求。如果建立时间或者保持时间的要求无法被满足，那么就会发生亚稳态现象。

        亚稳态(Metastability):如果数据传输中不满足触发器的Tsu和Th不满足，就可能产生亚稳态，此时触发器输出端Q在有效时钟沿之后比较长的一段时间处于不确定的状态，在这段时间里Q端在0和1之间处于振荡状态，而不是等于数据输入端D的值。这段时间称为决断时间Tmet (resolution time)。经过resolution time之后Q端将稳定到O或1上，但是稳定到O或者1，是随机的，与输入没有必然的关系。

13 恢复时间与去除时间

        恢复时间(Recovery Time)是指异步控制信号(如寄存器的异步清除和置位控制信号)在"下个时钟沿来临之前变无效的最小时间长度。这个时间的意义是，如果保证不了这个最小恢复时间，也就是说这个异步控制信号的解除与下个时钟沿'离得太近（但在这个时钟沿之前)，没有给寄存器留有足够时间来恢复至正常状态，那么就不能保证"下个时钟沿”能正常作用，也就是说这个时钟沿"可能会失效。
        去除时间(Removal)是指异步控制信号(如寄存器的异步清除和置位控制信号)在"有效时钟沿'之后变无效的最小时间长度。这个时间的意义是，如果保证不了这个去除时间，也就是说这个异步控制信号的解除与‘有效时钟沿'离得太近《但在这个时钟沿之后)，那么就不能保证有效地屏蔽这个“时钟沿”，也就是说这个“时钟沿"可能会起作用。
换句话来说，如果你想让某个时钟沿起作用，那么你就应该在"恢复时间'之前是异步控制信号变无效，如果你想让某个时钟沿不起作用，那么你就应该在“去除时间"过后使控制信号变无效。如果你的控制信号在这两种情况之间，那么就没法确定时钟沿是否起作用或不起作用了，也就是说可能会造成寄存器处于不确定的状态。而这些情况是应该避免的。所以恢复时间和去除时间是应该遵守的。
        比如下图中:复位信号rst_n作为一个异步控制型号，需要在下一个时钟有效沿之前就变无效（拉高)，以保证Recovery恢复时间，这样寄存器才有足够的时间恢复到正常状态(这有点类似建立时间);同样的，复位信号rst_n的移除不能与上一个时钟有效沿间隔太近，以保证其无法影响上—个时钟有效沿(这有点类似保持时间)。

14 4种基本的时序路径

下图是—张典型的FPGA与上游、下游器件通信的示意图。
 

其可以划分为基本的四条数据路径，这四条路径也是需要进行时序约束的最基本的路径。

1 管脚到寄存器
        路径1，上游器件通过FPGA管脚到FPGA的寄存器的时序路径，即pin2reg(管脚到寄存器)，需要对其进行约束，以满足FPGA端寄存器的建立时间和保持时间要求;

        路径1约束的是上游器件的源寄存器(起点)和FPGA内部的目的寄存器(终点)的数据路径，其目的是要满足后端即FPGA内部寄存器的建立时间要求和保持时间要求。
        路径1可以视为是路径2的一种，只不过路径1的源寄存器和目的寄存器都在FPGA内部，而路径2的源寄存器在上游器件中。

2 寄存器到寄存器
        路径2，FPGA内部的寄存器到另一个寄存器，即reg2reg(寄存器到寄存器)，需要对其进行约束，以满足FPGA端寄存器的建立时间和保持时间要求;

        路径2约束的是FPGA内部源寄存器（起点)和FPGA内部目的寄存器(终点)的数据路径，其目的是要通过提供要求的方式来使得综合工具vivado满足所有FPGA内部寄存器的建立时间要求和保持时间要求。
3 寄存器到管脚
        路径3，FPGA管脚到下游器件的寄存器的时序路径，即reg2pin(寄存器到管脚)，需要对其进行约束，以满足下游器件的寄存器的建立时间和保持时间要求;

        路径3约束的是FPGA内部的源寄存器（起点)和下游器件的目的寄存器(终点)的数据路径，其目的是要满足前端即FPGA内部寄存器的建立时间要求和保持时间要求。
        路径3同样可以视为是路径2的一种，只不过路径1的源寄存器和目的寄存器都在FPGA内部，而路径3的目的寄存器在下游器件中。
4 管脚到管教
        路径4，FPGA管脚到FPGA管脚的时序路径〈不通过任何寄存器)，其本质上是纯组合逻辑电路，仅仅需要约束其值在一个指定范围，不需要满足建立时间和保持时间要求。

        路径4中不存在任何寄存器，通常都是纯组合逻辑或者走线延迟等，所以也就不需要满足寄存器的建立时间要求和保持时间要求。需要的仅仅是根据开发需求约束其延迟的最小值和最大值。

15 发射沿(Launch Edge)与锁存沿(Latch Edge)

        路径1、2、3实际上都是对寄存器到寄存器之间的数据路径之间的约束，而路径4则是约束纯组合逻辑。
        由于寄存器的采样往往都发生在时钟的边沿，所以目的寄存器采样的值实际上是上个时钟周期的源寄存器的值，也就是说在源寄存器与目的寄存器之间其采样时间相差—个时钟周期。

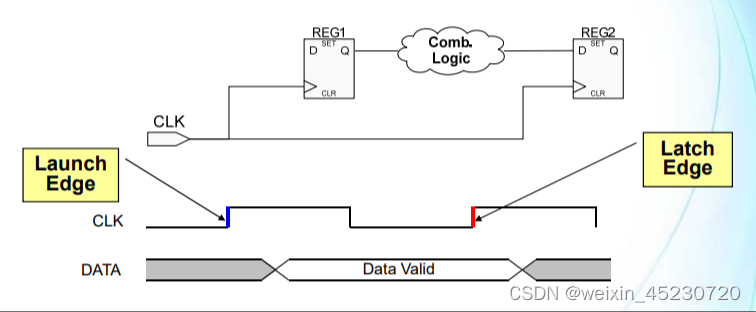
        发射沿（Launch Edge)∶是源寄存器采样的时间点，也是时序分析路径的起点。

        锁存沿(Latch Edge)︰是目的寄存器采样的时间点，也是时序分析路径的终点

16 数据到达时间(Data Arrival Time)

由于2个寄存器之间存在的组合逻辑和走线延迟等，使得在发射沿采样到的数据需要一定的时间才能到达后级的锁存沿，这个时间就被称为数据到达时间(Data Arrival Time) 。

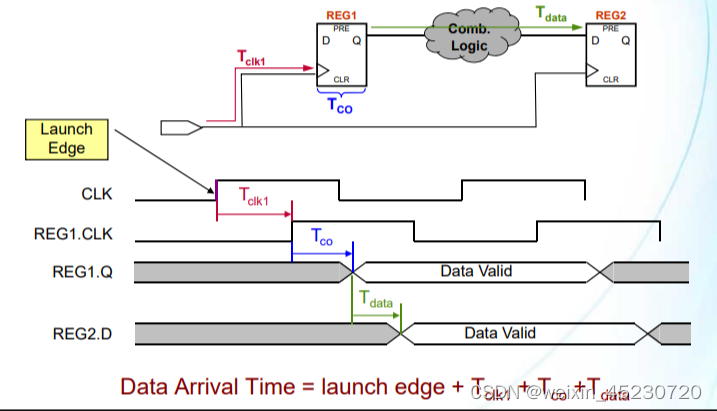
如上图，在计算数据到达时间时，存在3个时间参数:
        Tclk1:时钟信号从起点到达源寄存器REG1的时钟端口的时钟网络延时，产生原因一般是走线延迟
        Tco:源寄存器REG1内部的数据输出延迟，这个延迟时间是寄存器的固有属性，只和使用的FPGA芯片型号有关
        Tdata:数据从源寄存器REG1输出Q端到下级目的寄存器REG2的数据输入D之间的延时，一般是组合逻辑器件产生的固有延时和走线延时

        根据上图可以算出数据到达时间:Data Arrival Time = launch edge + Tclk1 + Tco +Tdata

17、数据需求时间--建立时间(Data Required Time - Setup)

时序约束的本质就是要满足所有寄存器的建立时间要求和保持时间要求，所以在数据经过一定的延迟从源寄存器到达目的寄存器后，同样需要满足目的寄存器的建立时间要求（Tsu) 。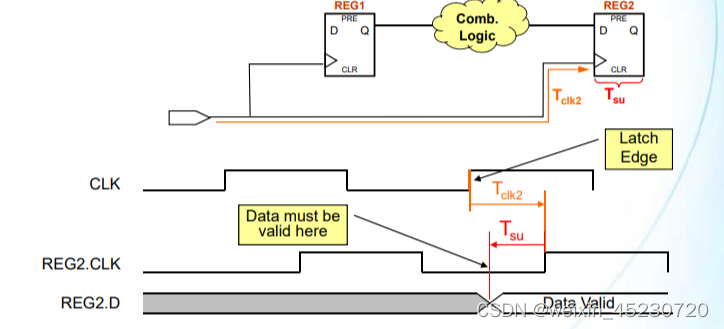

如上图，在计算数据需求时间--建立时间时，存在2个时间参数:
        Tclk2:时钟信号从起点到达目的寄存器REG2的时钟端口的时钟网络延时，产生原因一般是走线延迟
        Tsu:在时钟有效边沿到达之间，输入数据必须保持不变的时间，这意味着上级寄存器的输入至少要在这之前就保持稳定

        根据上图可以算出: Data Required Time + Tsu = latch edge +Tck2，即Data Required Time = latch edge + Tclk2- Tsu
        数据需求时间--建立时间，实际上是一种对数据到来之前数据保持稳定的最极端时间要求。比如为了满足目的寄存器的建立时间要求，计算得到上级寄存器的输出必须至少在3ns之前即保持稳定，这也就意味着上级数据能到达的最晚时间是3ns，那么1ns、2ns到达自然是可以的，

18 数据需求时间--保持时间(Data Required Time - Hold)

建立时间和保持时间是寄存器的2个固定需求属性，所以在数据经过一定的延迟从源寄存器到达目的寄存器后，同样需要满足目的寄存器的保持时间要求(Th) 。

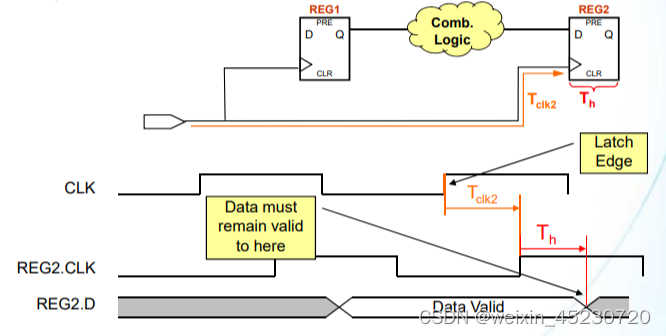
如上图，在计算数据需求时间--保持时间时，存在2个时间参数:
        Tclk2:时钟信号从起点到达目的寄存器REG2的时钟端口的时钟网络延时，产生原因一般是走线延迟
        Th:在时钟有效边沿到达之后，输入数据必须保持不变的时间，这意味着上级寄存器的输入至少要在这之后才能发生变化
        所以可以算出: Data Required Time = latch edge + Tclk2+ Th

19、建立时间裕量(Setup Slack)

        数据需求时间--建立时间实际上是一种对数据到来之前保持稳定的最极端的时间要求，比如为了满足目的寄存器的建立时间要求，计算得到上级寄存器的输出必须至少在时间刻度3ns之前即保持不变，这也就意味着上级数据能到达的最晚时间是3ns，那么1ns、2ns到达自然是可以的。
        如果数据在1ns即到达了目的寄存器，那么建立时间裕量就是3ns-1ns = 2ns，那么这个裕星有什么作用呢或者说代表着什么?前面我们知道到寄存器之间可能会存在一段组合逻辑和走线延迟，如果你的设计中某2个寄存器之间的建立时间裕量是2ns，则意味着你还有空间去折腾，比如寄存器彼此之间还可以增加一些组合逻辑器件或者更长的走线。

根据上图，可以算出: Setup Slack = Data Required Time-Data Arval Time，即Setup Slack = (latch edge + Tck2 - Tsu ) -(launch edge + Tck1 +Tco +Tdata ) = (latch edge - launch edge)+(Tclk2-Tck1 ) - (Tsu + Tco +Tdata) = Tperiod + Tskew-(Tsu + Tco +Tdata) 。
        如果Setup Slack为正，则说明数据在规定的时间内达到了目的寄存器;反之，则认为数据并没有在规定的时间达到目标，此时REG2锁存的数据很有可能是亚稳态状态。

20、保持时间裕量(Hold Slack)

数据需求时间--保持时间实际上是一种对时钟沿到来之后数据保持稳定的最极端的时间要求，比如为了满足目的寄存器的保持时间要求，计算得到上级寄存器的输出必须至少在时间刻度3ns之前都保持不变，这也就意味着上级数据能变化的最早时间是3ns，那么4ns,5ns到达自然是可以的。
如果数据在5ns处才在目的寄存器发生了变化，那么保持时间裕量就是5ns-3ns = 2ns。

根据上图，可以算出: Hold Slack = Data Arival Time - Data Required Time，即Hold Slack = (latch edge + Tck1 +Tco +Tdata)(latch edge + Tclk2 + Th) = (Tco +Tdata - Th) - (Tclk2 - Tck1) + (latch edge - latch edge) = (Tco +Tdata -Th) - Tskew。

        如果Hold Slack为正，则认为数据在被锁存的时候有足够多的稳定时间，是有效的;反之则认为数据可能是亚稳态状态。

21 、总结

搞明白了这些概念，那么静态时序分析9.其实也就很简单了。上文出现了很多的公式，看起来有点晦涩难懂，但是没关系，这些公示实际上仅仅是起到一个辅助理解时序分析的作用，并不需要去记忆，更也不需要熟练掌握这些公式来生搬硬套时序分析。因为现在的综合工具已经足够智能了，你只需要提出时序约束的要求，综合工具vivado自然会对这些路径——进行计算，你所要做的仅仅是找到时序裕量为负的路径并想办法改善即可。
此外，通过对上面公式的分析，可以让我们更好的了解静态时序分析的本质。

根据上文有（1)和(2）两式:
 

        建立时间裕量: Setup Slack = Tperiod + Tskew - (Tsu +Tco +Tdata)--- (1)

        保持时间裕量:Hold Slack = (Tco +Tdata - Th) - Tskew ----- (2)

其中，Tperiod是时钟周期;Tskew是寄存器之间的时钟偏差，产生的原因是时钟到达不同的寄存器的时钟端口有延迟;Tsu与Th分别是寄存器的建立时间要求和保持时间要求，这是寄存器的固有属性，只和FPGA的型号相关;Tco是从寄存器的输入端口到输出端口所需要的延时时间，同样是寄存器的固有属性;Tdata是寄存器之间的组合逻辑和走线延迟等之和，这与具体设计有关，平时我们大多都是通过减少Tdata来使得时间裕量为正，以此实现设计的时序收敛。
        Tskew实际上是一个可以被忽略掉的较小值，所以把它去掉，再对(1)和(2)两式做变形(Slack>0需被满足)，然后有(3)和(4）两式

                        Tperiod >(Tsu + Tco +Tdata) ---- (3)
                        (Tco +Tdata ) > Th ---- (4)

(3)）式子中的(Tsu +Tco +Tdata)代表数据从源寄存器到目的寄存器所消耗的时间，即（Tsu + Tco +Tdata)<Tperiod表示数据从源寄存器的采样时刻传到目的寄存器的采样时刻，不能超过一个时钟周期。如果数据传输超过一个时钟周期，那么就会导致目的寄存器器开始采样的时候，从源寄存器出发的数据还没有传过来。
对于(4）式可以两边同时加上Tsu ，得到(5)式:
                        (Tco +Tdata + Tsu ) >(Th + Tsu) ---- (5)

(5)式子中的(Tsu + Tco +Tdata)代表数据从源寄存器到目的寄存器所消耗的时间，(Th+TSu)是建立时间和保持时间之和,即寄存器的采样窗口时间。那么（Tsu +Tco +Tdala)> Th+Tsu表示数据从源寄存器的采样时刻传到目的寄存器的采样时刻，至少要大于寄存器的采样窗口。假如数据传输时间不大于采样窗口，则意味着数据的传输是特别快的，有可能目的寄存器开始采样时，源寄存器的采样仍没有结束，如果这个时候输入端数据有变化，那么不仅源寄存器处于亚稳态，目的寄存器也将处于亚稳态!
所以，数据传输延时既不能太大以至于超过一个时钟周期，也不能太小以至于小于触发器采样窗口的宽度。这就是静态时序分析的物理意义了。