一、原理
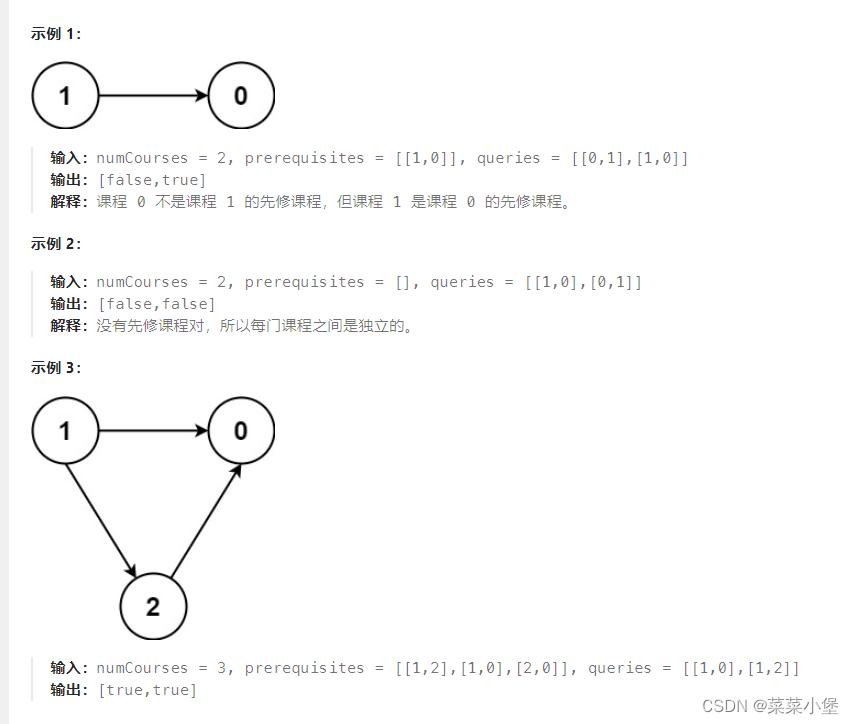
首先明确TSP问题的目标是什么,假设当前有3个城市,需要你从第一个城市开始,遍历所有城市,然后回到初始位置,要求总路径最短。这个时候就需要计算每个城市之间的两两距离,然后按顺序确定一条最短路径。
最稳妥的方案是,使用暴力枚举,列举出来所有的路线为1->2->3->1、1->3->2->1,然后计算一个最短路径即可。
但是当城市数量很多的时候,暴力枚举的方法计算量十分大,此时就需要考虑有没有简单一些的方法,虽然不是十分准确,但是能猜出一个大致的结果,即使不是最优解,只要接近最优结果也能接受。其他大部分智能优化算法都是这种思路,只是使用的具体思路有区别。
模拟退火算法,实际就是猜答案,然后从猜的结果中找个最优的结果输出,当猜的数量够大,结果就最接近实际结果。它会设置一个初始温度比较高例如1000,一个结束温度20,以一定函数从1000降低到20,然后设置一个迭代次数,每次迭代都会随机打乱路线,如果这个路线比之前的路线好,则直接把它作为最优路线,如果没有之前的好,则以一个很小的概率接受,这个概率也是通过随机数确定的,这里为什么要以一个很小的概率接受一个不好的结果呢?其实是为了防止结果陷入局部最优解,但是对于模拟退火这种猜答案的方式,个人感觉其实用不着以很小的概率接受一共不好的路线。
所以这个算法名字听起来不知所云,但是主要就是猜答案,也没有什么特殊的。
二、代码
//模拟退火算法(SA)求解TSP问题
/*类的体会2:
1.类外访问类中private方式:
①通过设置类中的public,get()函数,来获取一些变量值;
②对于数组的获取,一方面可以通过get(下标)函数来完成一对一的获取;
另一方面可以通过在类中public处声明类外的友元函数friend(对象),友元函数通过对象可以访问到private
2.类中函数要访问类外数据:
①全局变量可以直接访问;
②在类外创建该类的对象,通过对象调用函数,并传递类外数据参数;
③访问其他类还可以用友元函数
*/
#include<iostream>
#include<stdlib.h>
#include<time.h>
#include<math.h>
#include<vector>
#include<algorithm>
using namespace std;
#define T0 1000 //初始温度
#define T_end 20 //退出温度(环境温度)
#define q 0.9 //退火系数
#define L 10 //每个温度时的迭代次数,即链长
#define C 10 //城市数量
//10个城市的坐标:
double citys_position[C][2] =
{
{1304,2312},{3639,1315},{4177,2244},{3712,1399},{3488,1535},
{3326,1556},{3238,1229},{4196,1004},{4312,7900},{4386,570}
};
class Simulated_Annealing
{
private:
int i, j;
int Current_Solution[C]; //存放一个解
int Current_copy[C]; //存放解的副本,用于计算差异
double T = T0; //温度变量,并初始化
double f1, f2, df; //f1是初始解目标值,f2是新解目标值,df是新旧解目标值差
int count = 0; //记录降温次数(因为按系数退火,迭代次数不确定)
vector<vector<double>> All_soluitons; //存放每代中最后的解(也可以是全部解,加上链表迭代的)
vector<double> All_fitness; //存放每代中最后的解值
public:
/*《函数SA声明》:模拟退火主体功能*/
void SA();
/*《函数citys_generate声明》:初始化解*/
void citys_generate();
/*《函数Swap声明》:初始化解*/
void Swap(int* input_solution);
/*《Fitness函数声明:对传入解计算适应度值》*/
double Fitness(int* input_solution);
/*《distance函数声明:计算两两节点的距离,传入两个城市各自的坐标信息》*/
double distance(double* city1, double* city2);
/*《getCount函数:给外部调用count值》*/
int getCount() { return count; }
/*《getF1函数:给外部调用f1值》*/
int getF1() { return f1; }
/*《getCurrent_Solution函数:给外部调用该数组》*/
int getCurrent_Solution(int k)
{
return Current_Solution[k];
}
/*《get_All_solutions函数申明:定义为类中的友元函数,可以通过对象去访问类中的private。
注意:友元函数是可以访问类中的私有成员,但是得告诉他,他是哪个类的朋友。
是通过对象的传参来作过渡,而不能实现直接的访问,他找不到!》*/
friend void get_All_solutions(Simulated_Annealing &SA);
};
void main()
{
srand((unsigned)time(NULL));
time_t start, finish; //计时变量
start = clock(); //程序运行开始计时
/*《调用Simulated_Annealing类》*/
Simulated_Annealing SA1;
SA1.SA();
finish = clock(); //程序结束停止计时
//计算运行时间
double run_time = ((double)(finish - start)) / CLOCKS_PER_SEC;
//输出结果
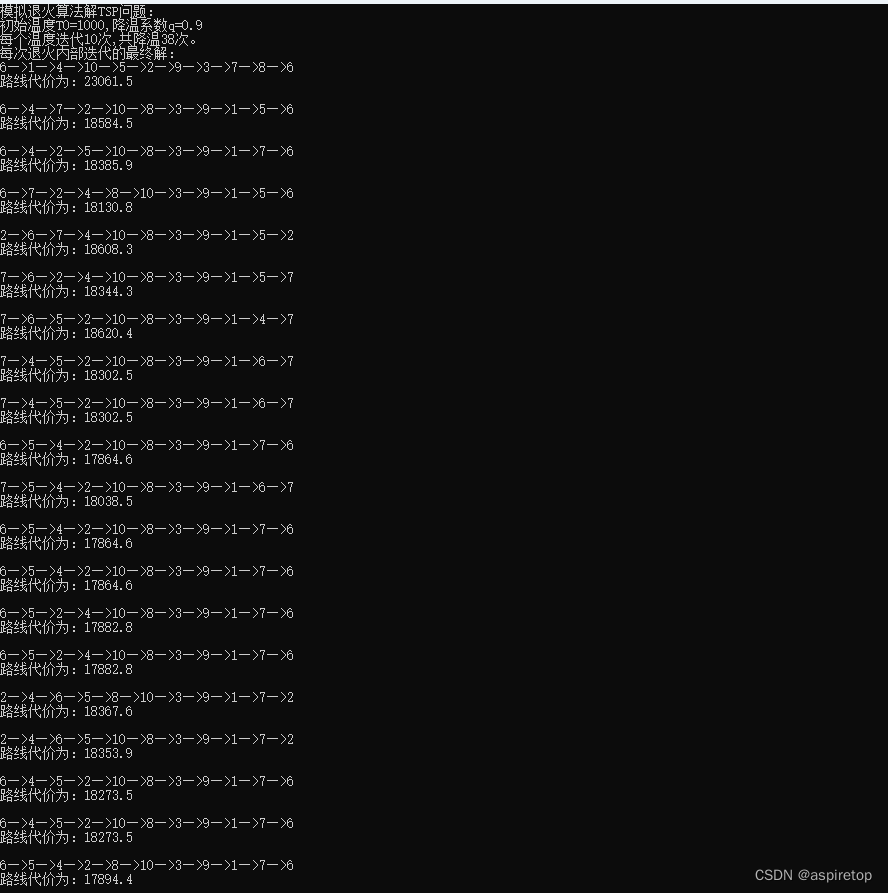
printf("模拟退火算法解TSP问题:\n");
cout << "初始温度T0=" << T0 << ",降温系数q=" << q << endl;
printf("每个温度迭代%d次,共降温%d次。\n", L, SA1.getCount());
/*《调用get_All_solutions函数:输出每次退火的方法和值,友元函数,可以通过对象去访问类中的private》*/
get_All_solutions(SA1);
printf("最终得TSP问题最优路径为:\n");
for (int j = 0; j < C - 1; j++)
{
printf("%d—>", SA1.getCurrent_Solution(j));
}
printf("%d—>", SA1.getCurrent_Solution(C - 1));
printf("%d\n", SA1.getCurrent_Solution(0));
cout << "最优路径长度为:" << SA1.getF1() << endl;
printf("程序运行耗时%1f秒.\n", run_time);
}
/*《函数SA定义》:模拟退火主体功能*/
void Simulated_Annealing::SA()
{
/*①《调用函数citys_generate》:初始化解*/
citys_generate();
/*《调用Fitness函数:对传入解计算适应度值》*/
f1 = Fitness(Current_Solution);//随机求解的一个代价值
while (T > T_end)//当温度低于结束温度时,退火结束
{
All_soluitons.push_back({}); //每代开始添加一个空行,存放本代结果值
All_fitness.push_back({}); //每代开始添加一个空行,存放本代代价值
for (i = 0; i < L; i++)//迭代次数5
{
//②复制初始解
for (j = 0; j < C; j++)
{
Current_copy[j] = Current_Solution[j];
}
/*③《调用Swap函数:对传入解做邻域搜索,两点交换》*/
Swap(Current_copy);//随机生成一个新的路线
/*④《调用Fitness函数:对传入解计算适应度值》*/
f2 = Fitness(Current_copy);//计算当前代价
df = f1 - f2;//当前代价和前一个代价差
/*退火原理:Metropolis准则,df<0*/
//⑤若新解>旧解值,df<0,则以概率 exp(df / T) 接受新解 df越大,指数越大。含义为新解效果越差,接受概率越小
if (df < 0)
{
//随机数(0,1),用于决定是否接受新解
double r;
r = (double)rand() / RAND_MAX; //分母32767
if (r < exp(df / T))//以很小的概率接受这个不好的解
{
//接受新解
for (j = 0; j < C; j++)
{
Current_Solution[j] = Current_copy[j];
}
f1 = f2;
}
}
//⑥若新解<=旧解值,df>=0,则直接接受新解
else//如果新解效果比较好,直接用这个新解
{
for (j = 0; j < C; j++)
{
Current_Solution[j] = Current_copy[j];
}
f1 = f2;
}
}
//⑦存放本次迭代的最后方案和适应值
for (int j = 0; j < C; j++)
{
All_soluitons[count].push_back(Current_Solution[j]);//每次迭代的路径存入vector
}
All_fitness[count] = f1;
//⑧以一定的速率降温
T *= q;//以1/2的速率减小
count++;
}
}
/*《函数citys_generate定义》:初始化解*/
void Simulated_Annealing::citys_generate()
{
//①一个城市序列
vector<int> temp_city;
for (int i = 0; i < C; i++)//城市数量
{
temp_city.push_back(i + 1);
}
//②打乱
random_shuffle(temp_city.begin(), temp_city.end());//均匀分布来随机移动元素
//③赋值给Current_Solution
for (int j = 0; j < temp_city.size(); j++)
{
Current_Solution[j] = temp_city[j];//初始为随机解
}
}
/*《函数Swap定义》:初始化解*/
void Simulated_Annealing::Swap(int* input_solution)
{
//①生成交换节点下标
int point1 = rand() % C;//交换点1
int point2 = rand() % C;//交换点2
while (point1 == point2)
{
point2 = rand() % C;//保证交换点不同
}
//②交换
swap(input_solution[point1], input_solution[point2]);//随机交换最终路径的航点
}
/*《Fitness函数定义:对传入解计算适应度值》*/
double Simulated_Annealing::Fitness(int* input_solution)//代价函数
{
//初始化路径长度
double cost = 0;
//从第一个城市遍历到最后一个城市
for (int j = 0; j < C - 1; j++)
{
/*《调用distance函数:计算两两节点的距离,传入两个城市各自的坐标信息》*/
int k = input_solution[j];//城市序号-1=城市位置下标 第二个参数为第二个城市的位置
cost += distance(citys_position[input_solution[j] - 1], citys_position[input_solution[j + 1] - 1]);//初始位置为第一个城市
}
//从最后一个城市回到第一个城市
cost += distance(citys_position[input_solution[C - 1] - 1], citys_position[input_solution[0] - 1]);
return cost;
}
/*《distance函数声明:计算两两节点的距离,传入两个城市各自的坐标信息》*/
double Simulated_Annealing::distance(double* city1, double* city2)
{
/*计算相邻两城市间距离*/
double x1 = city1[0]; //城市1横坐标
double y1 = city1[1];
double x2 = city2[0];
double y2 = city2[1]; //城市2纵坐标
double dist = pow((pow((x1 - x2), 2) + pow((y1 - y2), 2)), 0.5);
return dist; //返回距离值
}
/*《get_All_solutions函数申明:定义为类中的友元函数,通过对象可以访问类中的向量》*/
void get_All_solutions(Simulated_Annealing &SA)
{
cout << "每次退火内部迭代的最终解:" << endl;
for (int i = 0; i < SA.All_soluitons.size(); i++)
{
for (int j = 0; j < SA.All_soluitons[i].size(); j++)
{
cout << SA.All_soluitons[i][j] << "—>";
}
cout << SA.All_soluitons[i][0] << endl;
cout << "路线代价为:" << SA.All_fitness[i] << std::endl << std::endl;
}
}




![[其他]IDEA中Maven项目配置国内源](https://img-blog.csdnimg.cn/773f990abefe4a36ac7bb8536b7cea4e.png)