并查集基础
一、概念及其介绍
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。
并查集的思想是用一个数组表示了整片森林(parent),树的根节点唯一标识了一个集合,我们只要找到了某个元素的的树根,就能确定它在哪个集合里。
二、适用说明
并查集用在一些有 N 个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这个过程看似并不复杂,但数据量极大,若用其他的数据结构来描述的话,往往在空间上过大,计算机无法承受,也无法在短时间内计算出结果,所以只能用并查集来处理。
三、并查集的基本数据表示

如上图 0-4 下面都是 0,5-9 下面都是 1,表示 0、1、2、3、4 这五个元素是相连接的,5、6、7、8、9 这五个元素是相连的。
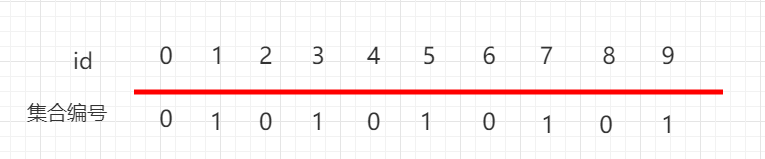
再如上图 0、2、4、6、8 下面都是 0 这个集合,表示 0、2、4、6、8 这五个元素是相连接的,1、3、5、7、9 下面都是 1 这个集合,表示 0,1、3、5、7、9 这五个元素是相连的。
构造一个类 UnionFind,初始化, 每一个id[i]指向自己, 没有合并的元素:
...
public UnionFind1(int n) {
count = n;
id = new int[n];
// 初始化, 每一个id[i]指向自己, 没有合并的元素
for (int i = 0; i < n; i++)
id[i] = i;
}
...
Java 实例代码
源码包下载:Download
UnionFind.java 文件代码:
package runoob.union;
public class UnionFind{
private int[] id;
// 数据个数
private int count;
public UnionFind1(int n) {
count = n;
id = new int[n];
for (int i = 0; i < n; i++)
id[i] = i;
}
}
二分搜索树的特性
一、顺序性
二分搜索树可以当做查找表的一种实现。
我们使用二分搜索树的目的是通过查找 key 马上得到 value。minimum、maximum、successor(后继)、predecessor(前驱)、floor(地板)、ceil(天花板、rank(排名第几的元素)、select(排名第n的元素是谁)这些都是二分搜索树顺序性的表现。
二、局限性
二分搜索树在时间性能上是具有局限性的。
如下图所示,元素节点一样,组成两种不同的二分搜索树,都是满足定义的:
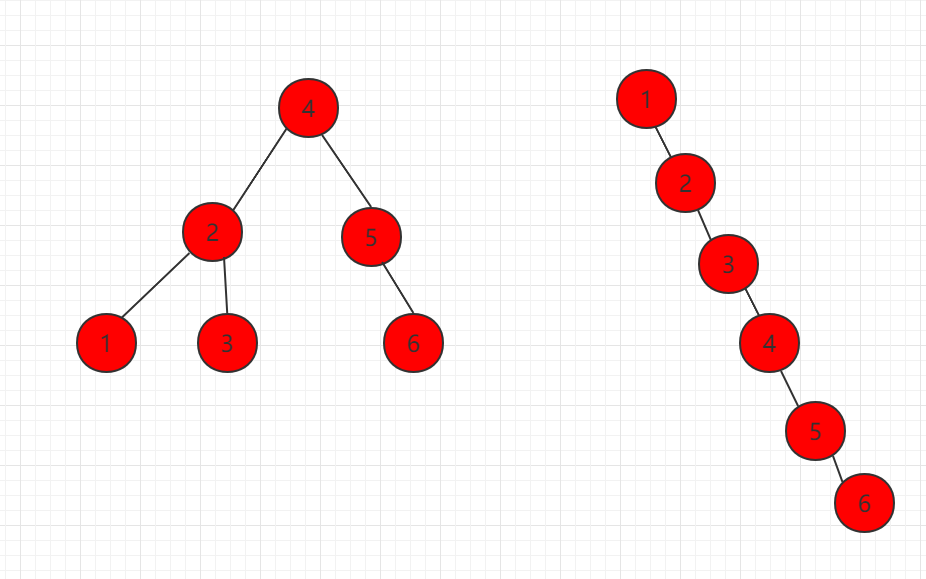
二叉搜索树可能退化成链表,相应的,二叉搜索树的查找操作是和这棵树的高度相关的,而此时这颗树的高度就是这颗树的节点数 n,同时二叉搜索树相应的算法全部退化成 O(n) 级别。