机器学习笔记之最优化理论与方法——关于共轭方向法重要特征的相关证明
- 引言
- 回顾:共轭方向法的思想与几何解释
- 共轭方向法的重要特征(2023/9/12)
- 共轭方向法重要特征的证明
引言
上一节介绍了共轭方向法的朴素思想与几何意义。本节将继续介绍共轭方向法的重要特征以及相关证明。
回顾:共轭方向法的思想与几何解释
共轭方向法的基本思想是:针对凸二次函数的优化问题:
min
f
(
x
)
=
1
2
x
T
Q
x
+
C
T
x
,
Q
≻
0
\begin{aligned}\min f(x) = \frac{1}{2} x^T \mathcal Q x + \mathcal C^T x ,\mathcal Q \succ 0\end{aligned}
minf(x)=21xTQx+CTx,Q≻0,基于正定矩阵
Q
\mathcal Q
Q,构建一个由两两共轭的向量组成的向量组
D
=
{
d
0
,
d
1
,
⋯
,
d
n
−
1
}
\mathcal D = \{d_0,d_1,\cdots,d_{n-1}\}
D={d0,d1,⋯,dn−1}:
∀
d
i
,
d
j
∈
D
;
i
≠
j
⇒
(
d
i
)
T
Q
d
j
=
0
\forall d_i,d_j \in \mathcal D;i \neq j \Rightarrow (d_i)^T \mathcal Q d_j = 0
∀di,dj∈D;i=j⇒(di)TQdj=0
并令:
x
k
+
1
=
x
k
+
∑
i
=
0
n
−
1
α
i
⋅
d
i
x_{k+1} = x_{k} + \sum_{i=0}^{n-1}\alpha_i \cdot d_i
xk+1=xk+i=0∑n−1αi⋅di
其中
α
i
(
i
=
0
,
1
,
2
,
⋯
,
n
−
1
)
\alpha_i(i=0,1,2,\cdots,n-1)
αi(i=0,1,2,⋯,n−1)满足:
α
i
=
arg
min
α
ϕ
(
α
)
=
arg
min
α
f
(
x
k
+
α
⋅
d
i
)
\alpha_i = \mathop{\arg\min}\limits_{\alpha} \phi(\alpha) = \mathop{\arg\min}\limits_{\alpha} f(x_k + \alpha \cdot d_i)
αi=αargminϕ(α)=αargminf(xk+α⋅di)
从而通过坐标轴交替下降法执行
n
n
n次迭代,完成一次线搜索过程。
从几何意义的角度解释:记
S
=
(
d
0
,
d
1
,
⋯
,
d
n
−
1
)
n
×
n
\mathcal S = (d_0,d_1,\cdots,d_{n-1})_{n \times n}
S=(d0,d1,⋯,dn−1)n×n。根据共轭方向的定义,必然有
S
T
Q
S
\mathcal S^T \mathcal Q \mathcal S
STQS是一个对角矩阵:
{
(
d
i
)
T
Q
d
j
=
0
∀
d
i
,
d
j
∈
S
;
i
≠
j
S
T
Q
S
=
[
(
d
i
)
T
Q
d
j
]
n
×
n
=
[
(
d
1
)
T
Q
d
1
0
⋯
0
0
(
d
2
)
T
Q
d
2
⋯
0
⋮
⋮
⋱
⋮
0
0
⋯
(
d
n
−
1
)
T
Q
d
n
−
1
]
=
Λ
\begin{cases} (d_i)^T \mathcal Q d_j = 0 \quad \forall d_i,d_j \in \mathcal S;i \neq j \\ \quad \\ \mathcal S^T \mathcal Q \mathcal S = [(d_i)^T \mathcal Q d_j]_{n \times n} = \begin{bmatrix} (d_1)^T\mathcal Qd_1 & 0 & \cdots & 0 \\ 0 & (d_2)^T \mathcal Q d_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & (d_{n-1})^T \mathcal Qd_{n-1} \end{bmatrix} = \Lambda \end{cases}
⎩
⎨
⎧(di)TQdj=0∀di,dj∈S;i=jSTQS=[(di)TQdj]n×n=
(d1)TQd10⋮00(d2)TQd2⋮0⋯⋯⋱⋯00⋮(dn−1)TQdn−1
=Λ
根据这个性质,可以对正定矩阵
Q
\mathcal Q
Q进行对角化,从而将
f
(
x
)
f(x)
f(x)变成一个标准型。具体方法如下:
- 由于
d
0
,
d
1
,
⋯
,
d
n
−
1
d_0,d_1,\cdots,d_{n-1}
d0,d1,⋯,dn−1向量两两共轭,必然也是两两线性无关。因而矩阵
S
\mathcal S
S是一个可逆矩阵。对决策变量
x
∈
R
n
x \in \mathbb R^n
x∈Rn使用
S
\mathcal S
S进行投影,得到新的向量
x
^
\hat {x}
x^;从而将
f
(
x
)
f(x)
f(x)变成关于
x
^
\hat{x}
x^的函数形式
f
^
(
x
^
)
\hat f(\hat {x})
f^(x^):
{ x = S ⋅ x ^ ⇔ x ^ = S − 1 x f ( x ) = 1 2 x T Q x + C T x = 1 2 [ x ^ ] T S T Q S ⋅ x ^ + ( S T C ) T x = f ^ ( x ^ ) \begin{cases} x = \mathcal S \cdot \hat {x} \Leftrightarrow \hat {x} = \mathcal S^{-1} x\\ \quad \\ \begin{aligned} f(x) & = \frac{1}{2} x^T \mathcal Q x + \mathcal C^T x \\ & = \frac{1}{2} [\hat {x}]^T \mathcal S^T \mathcal Q \mathcal S \cdot \hat {x} + (\mathcal S^T \mathcal C)^T x = \hat f(\hat {x}) \end{aligned} \end{cases} ⎩ ⎨ ⎧x=S⋅x^⇔x^=S−1xf(x)=21xTQx+CTx=21[x^]TSTQS⋅x^+(STC)Tx=f^(x^) - 此时的
f
^
(
x
^
)
\hat f(\hat {x})
f^(x^)是一个标准型。对应的,将线搜索过程中的数值解使用
S
\mathcal S
S进行投影,可以得到如下结果:
{ x ^ k = S − 1 x k x ^ k + 1 = S − 1 x k + 1 = S − 1 ( x k + ∑ i = 0 n − 1 α i ⋅ d i ) = S − 1 x k + ∑ i = 0 n − 1 α i ⋅ S − 1 d i \begin{cases} \hat {x}_k = \mathcal S^{-1} x_k \\ \begin{aligned} \hat x_{k+1} & = \mathcal S^{-1} x_{k+1} \\ & = \mathcal S^{-1} \left(x_{k} + \sum_{i=0}^{n-1}\alpha_i \cdot d_i\right) \\ & = \mathcal S^{-1} x_k + \sum_{i=0}^{n-1} \alpha_i \cdot \mathcal S^{-1} d_i \end{aligned} \end{cases} ⎩ ⎨ ⎧x^k=S−1xkx^k+1=S−1xk+1=S−1(xk+i=0∑n−1αi⋅di)=S−1xk+i=0∑n−1αi⋅S−1di
由于 S − 1 S = I \mathcal S^{-1} \mathcal S = \mathcal I S−1S=I,从而 S − 1 d i ( i = 0 , 1 , ⋯ , n − 1 ) \mathcal S^{-1}d_i(i=0,1,\cdots,n-1) S−1di(i=0,1,⋯,n−1)表示单位坐标向量 e i + 1 e_{i+1} ei+1。将其代入有:
x k + 1 = x k + ∑ i = 0 n − 1 α i ⋅ d i ⇔ x ^ k + 1 = x ^ k + ∑ i = 0 n − 1 α i ⋅ e i + 1 x_{k+1} = x_{k} + \sum_{i=0}^{n-1}\alpha_i \cdot d_i \Leftrightarrow \hat x_{k+1} = \hat x_k + \sum_{i=0}^{n-1} \alpha_i \cdot e_{i+1} xk+1=xk+i=0∑n−1αi⋅di⇔x^k+1=x^k+i=0∑n−1αi⋅ei+1
最终可用坐标轴交替下降法对数值解序列进行求解。上述算法的关键在于:该算法必须在共轭方向 d 0 , d 1 , ⋯ , d n − 1 d_0,d_1,\cdots,d_{n-1} d0,d1,⋯,dn−1已知的条件下。本节将重点介绍:如何获取共轭方向 d i d_i di。
共轭方向法的重要特征(2023/9/12)
由于
f
(
x
)
=
1
2
x
T
Q
x
+
C
T
x
,
Q
≻
0
\begin{aligned}f(x) = \frac{1}{2} x^T \mathcal Q x + \mathcal C^T x,\mathcal Q \succ 0\end{aligned}
f(x)=21xTQx+CTx,Q≻0是凸二次函数,基于初始点
x
0
x_0
x0以及关于正交矩阵
Q
\mathcal Q
Q的共轭方向
d
k
(
k
=
0
,
1
,
2
,
⋯
,
n
−
1
)
d_k(k=0,1,2,\cdots,n-1)
dk(k=0,1,2,⋯,n−1),算法的线搜索过程以及各迭代步骤的最优步长
α
k
(
k
=
0
,
1
,
2
,
⋯
,
n
−
1
)
\alpha_k(k=0,1,2,\cdots,n-1)
αk(k=0,1,2,⋯,n−1)表示如下:
{
x
k
+
1
=
x
k
+
α
k
⋅
d
k
α
k
=
−
[
∇
f
(
x
k
)
]
T
d
k
(
d
k
)
T
Q
d
k
k
=
0
,
1
,
2
,
⋯
,
n
−
1
\begin{cases} x_{k+1} = x_k + \alpha_k \cdot d_k \\ \quad \\ \begin{aligned} \alpha_k = - \frac{[\nabla f(x_k)]^T d_k}{(d_k)^T \mathcal Q d_k} \quad k=0,1,2,\cdots,n-1 \end{aligned} \end{cases}
⎩
⎨
⎧xk+1=xk+αk⋅dkαk=−(dk)TQdk[∇f(xk)]Tdkk=0,1,2,⋯,n−1
这里需要做一些说明。上面的描述是文章下面链接中视频的描述(37:25)。很明显,它将线搜索迭代过程的下标
k
k
k与共轭方向迭代过程的下标
i
i
i全部归为下标
k
k
k,真实情况应该是下面描述:
{
x
k
+
1
=
x
k
+
α
i
⋅
d
i
α
i
=
−
[
∇
f
(
x
k
)
]
T
d
i
(
d
i
)
T
Q
d
i
{
i
=
0
,
1
,
2
,
⋯
,
n
−
1
k
=
0
,
1
,
2
,
⋯
,
∞
\begin{cases} x_{k+1} = x_k + \alpha_i \cdot d_i \\ \quad \\ \begin{aligned} \alpha_i = - \frac{[\nabla f(x_k)]^T d_i}{(d_i)^T \mathcal Q d_i} \end{aligned} \end{cases}\begin{cases} i=0,1,2,\cdots,n-1 \\ k = 0,1,2,\cdots, \infty \end{cases}
⎩
⎨
⎧xk+1=xk+αi⋅diαi=−(di)TQdi[∇f(xk)]Tdi{i=0,1,2,⋯,n−1k=0,1,2,⋯,∞
从这组公式可以看出:只有决策变量
x
k
∈
R
n
x_k \in \mathbb R^n
xk∈Rn各分量均迭代一次后,
x
k
⇒
x
k
+
1
x_k \Rightarrow x_{k+1}
xk⇒xk+1。但视频中的写法也没有错,因为凸二次函数
f
(
x
)
f(x)
f(x)可以通过一步
k
:
0
⇒
1
k:0 \Rightarrow 1
k:0⇒1即可完成迭代。而这一步存在
n
n
n次迭代,因而在该简单情况下,视频中将下标
i
,
k
i,k
i,k合并,并描述成
n
n
n次迭代。这样做的好处在于:第
k
k
k次迭代描述的是共轭方向
d
k
d_k
dk的迭代过程。后续均使用视频中的方式进行描述。
基于上面描述产生的数值解序列 { x k } k = 1 n \{x_k\}_{k=1}^{n} {xk}k=1n具有如下特征:
-
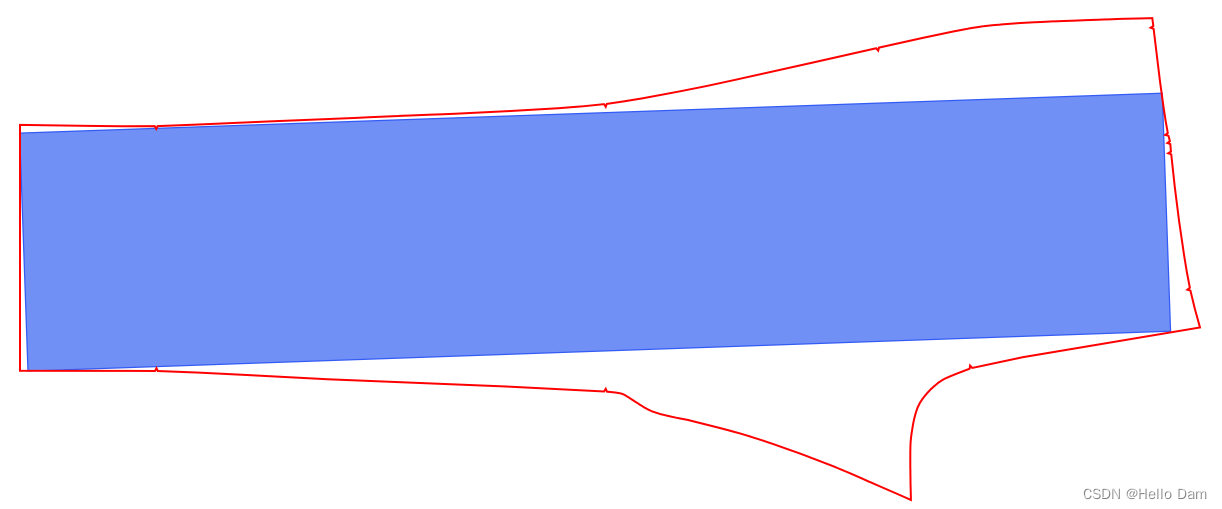
在第 k ( k = 1 , 2 , ⋯ , n ) k(k=1,2,\cdots,n) k(k=1,2,⋯,n)次迭代产生的迭代结果 x k x_k xk,其梯度方向 ∇ f ( x k ) \nabla f(x_k) ∇f(xk)与之前使用过的共轭方向 d i ( i = 0 , 1 , ⋯ , k − 1 ) d_i(i=0,1,\cdots,k-1) di(i=0,1,⋯,k−1)均垂直:
[ ∇ f ( x k ) ] T d i = 0 i = 0 , 1 , 2 , ⋯ , k − 1 [\nabla f(x_k)]^T d_i = 0 \quad i=0,1,2,\cdots,k-1 [∇f(xk)]Tdi=0i=0,1,2,⋯,k−1
对应示例图像表示如下:
很明显,从初始点x ( 0 ) x^{(0)} x(0)开始,沿着共轭方向 d ( 1 ) d^{(1)} d(1)更新至x ( 1 ) x^{(1)} x(1);其中∇ f ( x ( 1 ) ) \nabla f(x^{(1)}) ∇f(x(1))描述方向与d ( 1 ) d^{(1)} d(1)描述方向相垂直;由于x ( 2 ) x^{(2)} x(2)是最优解,其∇ f ( x ( 2 ) ) = 0 \nabla f(x^{(2)}) = 0 ∇f(x(2))=0。从而与d ( 1 ) , d ( 2 ) d^{(1)},d^{(2)} d(1),d(2)均垂直。

-
经过 k k k次迭代得到的位置 x k = x 0 + ∑ i = 0 k − 1 α i ⋅ d i x_k = x_0 + \sum_{i=0}^{k-1} \alpha_i \cdot d_i xk=x0+∑i=0k−1αi⋅di,可以将该结果描述为如下形式:
{ x k = arg min { 1 2 x T Q x + C T x ∣ x ∈ X k } X k = { x 0 + ∑ i = 0 k − 1 α i ⋅ d i ∣ α i ∈ R } \begin{cases} \begin{aligned} & x_k = \mathop{\arg\min} \left\{\frac{1}{2} x^T \mathcal Q x + \mathcal C^T x \mid x \in \mathcal X_k\right\} \\ & \mathcal X_k = \left\{x_0 + \sum_{i=0}^{k-1} \alpha_i \cdot d_i \mid \alpha_i \in \mathbb R\right\} \end{aligned} \end{cases} ⎩ ⎨ ⎧xk=argmin{21xTQx+CTx∣x∈Xk}Xk={x0+i=0∑k−1αi⋅di∣αi∈R}
说明:关于x k x_k xk对应的可选择范围 X k \mathcal X_k Xk,其对应的共轭方向 d 0 , ⋯ , d k − 1 d_0,\cdots,d_{k-1} d0,⋯,dk−1并未出现调整,只是将对应的步长α 0 , ⋯ , α k − 1 \alpha_0,\cdots,\alpha_{k-1} α0,⋯,αk−1均作为变量,从而构成位置空间X k \mathcal X_k Xk,而x k x_k xk是位置空间中使目标函数f ( x ) f(x) f(x)最小的位置点。当k = n k=n k=n时,此时对应的位置空间X n \mathcal X_n Xn就是完整的特征空间R n \mathbb R^n Rn。当然,这里描述的完整特征空间是由共轭方向 d 0 , d 1 , ⋯ , d n d_0,d_1,\cdots,d_n d0,d1,⋯,dn构成的投影空间,而不是原始特征空间。
x n = arg min { 1 2 x T Q x + C T x ∣ x ∈ R n } \begin{aligned}x_n = \mathop{\arg\min}\limits \left\{\frac{1}{2} x^T \mathcal Q x + \mathcal C^T x \mid x \in \mathbb R^n\right\}\end{aligned} xn=argmin{21xTQx+CTx∣x∈Rn}
根据上式可以看出,关于f ( x ) f(x) f(x)必然可以通过最多 n n n步找到最优解。
共轭方向法重要特征的证明
关于 [ ∇ f ( x k ) ] T d i ( i = 1 , 2 , ⋯ , k − 1 ) [\nabla f(x_k)]^T d_i(i=1,2,\cdots,k-1) [∇f(xk)]Tdi(i=1,2,⋯,k−1)的证明:
-
当 i = k − 1 i=k-1 i=k−1时,对应迭代步骤的步长 α k − 1 \alpha_{k-1} αk−1可表示为:
该式中仅包含α \alpha α一个变量,记作ϕ k − 1 ( α ) \phi_{k-1}(\alpha) ϕk−1(α)。
α k − 1 = arg min α f ( x k − 1 + α ⋅ d k − 1 ) = arg min α ϕ k − 1 ( α ) \alpha_{k-1} = \mathop{\arg\min}\limits_{\alpha} f(x_{k-1} + \alpha \cdot d_{k-1}) = \mathop{\arg\min}\limits_{\alpha}\phi_{k-1}(\alpha) αk−1=αargminf(xk−1+α⋅dk−1)=αargminϕk−1(α)
上式可等价为:
根据线搜索公式:x k = x k − 1 + α k − 1 ⋅ d k − 1 x_k = x_{k-1} + \alpha_{k-1} \cdot d_{k-1} xk=xk−1+αk−1⋅dk−1可知∇ f ( x k − 1 + α k − 1 ⋅ d k − 1 ) \nabla f(x_{k-1} + \alpha_{k-1} \cdot d_{k-1}) ∇f(xk−1+αk−1⋅dk−1)就是函数f ( ⋅ ) f(\cdot) f(⋅)在x k x_k xk处的梯度:∇ f ( x k ) \nabla f(x_k) ∇f(xk)。
0 ≜ ∇ ϕ k − 1 ( α k − 1 ) = ∂ ϕ k − 1 ( α ) ∂ α ∣ α = α k − 1 = [ ∇ f ( x k − 1 + α k − 1 ⋅ d k − 1 ) ] T d k − 1 = [ ∇ f ( x k ) ] T d k − 1 \begin{aligned} 0 & \triangleq \nabla \phi_{k-1}(\alpha_{k-1}) \\ & = \frac{\partial \phi_{k-1}(\alpha)}{\partial \alpha} \mid_{\alpha = \alpha_{k-1}} \\ & = [\nabla f(x_{k-1} + \alpha_{k-1} \cdot d_{k-1})]^T d_{k-1} \\ & = [\nabla f(x_k)]^T d_{k-1} \end{aligned} 0≜∇ϕk−1(αk−1)=∂α∂ϕk−1(α)∣α=αk−1=[∇f(xk−1+αk−1⋅dk−1)]Tdk−1=[∇f(xk)]Tdk−1
可以看出:第 k − 1 k-1 k−1次迭代产生的输出位置 x k x_k xk,其梯度 ∇ f ( x k ) \nabla f(x_k) ∇f(xk)与 k − 1 k-1 k−1次迭代使用的共轭方向 d k − 1 d_{k-1} dk−1垂直。同理:当 k = 1 , 2 , ⋯ , n k=1,2,\cdots,n k=1,2,⋯,n时,该结论均成立。 -
上面仅仅是描述:同一次迭代,其产生的输出位置与共轭方向之间是垂直关系;若非同一次迭代,观察内积 [ ∇ f ( x k ) ] T d i ( i = 0 , 1 , 2 , ⋯ , k − 2 ) [\nabla f(x_k)]^T d_i(i=0,1,2,\cdots,k-2) [∇f(xk)]Tdi(i=0,1,2,⋯,k−2):
将∇ f ( x k ) = Q x k + C \nabla f(x_k) = \mathcal Q x_k + \mathcal C ∇f(xk)=Qxk+C代入。将x k x_k xk视作从第i + 1 i+1 i+1次迭代开始,一直到k − 1 k-1 k−1次迭代产生的输出位置。这里可能并没有取出所有的迭代步骤,仅选择从i + 1 i+1 i+1到k − 1 k-1 k−1这一迭代部分。对应线搜索过程表示如下:
x k = x i + 1 + α i + 1 ⋅ d i + 1 + ⋯ + α k − 1 ⋅ d k − 1 x_k = x_{i+1} + \alpha_{i+1} \cdot d_{i+1} + \cdots + \alpha_{k-1} \cdot d_{k-1} xk=xi+1+αi+1⋅di+1+⋯+αk−1⋅dk−1根据向量共轭的定义:∀ d i , d j ∈ D ; i ≠ j ⇒ ( d i ) T Q d j = 0 \forall d_i,d_j \in \mathcal D;i \neq j \Rightarrow (d_i)^T \mathcal Q d_j = 0 ∀di,dj∈D;i=j⇒(di)TQdj=0,消除掉展开式中的无关项;i + 1 , ⋯ , k − 1 ≠ i i+1,\cdots,k-1 \neq i i+1,⋯,k−1=i恒成立;且Q T = Q \mathcal Q^T = \mathcal Q QT=Q。
[ ∇ f ( x k ) ] T d i = ( Q x k + C ) T d i = [ Q ( x i + 1 + α i + 1 ⋅ d i + 1 + ⋯ + α k − 1 d k − 1 ) + C ] T d i = [ Q x i + 1 + α i + 1 Q ⋅ d i + 1 + ⋯ + α k − 1 Q ⋅ d k − 1 + C ] T d i = [ Q x i + 1 ] T d i + α i + 1 ( d i + 1 ) T Q T d i ⏟ = 0 + ⋯ + α k − 1 ( d k − 1 ) T Q T d i ⏟ = 0 + C T d i = [ Q x i + 1 + C ] T d i = [ ∇ f ( x i + 1 ) ] T d i \begin{aligned} [\nabla f(x_k)]^T d_i & = (\mathcal Q x_k +\mathcal C)^T d_i \\ & = [\mathcal Q (x_{i+1} + \alpha_{i+1} \cdot d_{i+1} + \cdots + \alpha_{k-1} d_{k-1}) + \mathcal C]^T d_i \\ & = [\mathcal Q x_{i+1} + \alpha_{i+1} \mathcal Q \cdot d_{i+1} + \cdots + \alpha_{k-1} \mathcal Q \cdot d_{k-1} + \mathcal C]^T d_i \\ & = [\mathcal Q x_{i+1}]^Td_i + \underbrace{\alpha_{i+1} (d_{i+1})^T \mathcal Q^T d_i}_{=0} + \cdots + \underbrace{\alpha_{k-1}(d_{k-1})^T \mathcal Q^T d_i}_{=0} + \mathcal C^Td_i \\ & = [\mathcal Q x_{i+1} + \mathcal C]^T d_{i} \\ & = [\nabla f(x_{i+1})]^T d_i \end{aligned} [∇f(xk)]Tdi=(Qxk+C)Tdi=[Q(xi+1+αi+1⋅di+1+⋯+αk−1dk−1)+C]Tdi=[Qxi+1+αi+1Q⋅di+1+⋯+αk−1Q⋅dk−1+C]Tdi=[Qxi+1]Tdi+=0 αi+1(di+1)TQTdi+⋯+=0 αk−1(dk−1)TQTdi+CTdi=[Qxi+1+C]Tdi=[∇f(xi+1)]Tdi
当 i = k − 1 i=k-1 i=k−1时,上面已经证明过,因而有: [ ∇ f ( x i + 1 ) ] T d i = 0 [\nabla f(x_{i+1})]^T d_i = 0 [∇f(xi+1)]Tdi=0
从而得到结论:即便不是同一次迭代,其迭代产生位置的梯度 ∇ f ( x k ) \nabla f(x_k) ∇f(xk)与使用过的共轭方向 d 0 , d 1 , ⋯ , d k − 1 d_0,d_1,\cdots,d_{k-1} d0,d1,⋯,dk−1同样存在垂直关系。
关于 { x k = arg min { 1 2 x T Q x + C T x ∣ x ∈ X k } X k = { x 0 + ∑ i = 0 k − 1 α i ⋅ d i ∣ α i ∈ R , i = 1 , 2 , ⋯ , k − 1 } \begin{cases} \begin{aligned} & x_k = \mathop{\arg\min} \left\{\frac{1}{2} x^T \mathcal Q x + \mathcal C^T x \mid x \in \mathcal X_k\right\} \\ & \mathcal X_k = \left\{x_0 + \sum_{i=0}^{k-1} \alpha_i \cdot d_i \mid \alpha_i \in \mathbb R,i=1,2,\cdots,k-1\right\} \end{aligned} \end{cases} ⎩ ⎨ ⎧xk=argmin{21xTQx+CTx∣x∈Xk}Xk={x0+i=0∑k−1αi⋅di∣αi∈R,i=1,2,⋯,k−1}的证明:
- 将
x
k
x_k
xk使用线搜索公式进行表述:
x k = x 0 + α 0 ⋅ d 0 ⏟ x 1 + α 1 ⋅ d 1 ⏟ x 2 + ⋯ + α k − 1 ⋅ d k − 1 = x 0 + ∑ i = 0 k − 1 α i ⋅ d i \begin{aligned} x_k & = \underbrace{\underbrace{x_0 + \alpha_0 \cdot d_0}_{x_1} + \alpha_1 \cdot d_1}_{x_2}+\cdots + \alpha_{k-1} \cdot d_{k-1} \\ & = x_0 + \sum_{i=0}^{k-1} \alpha_i \cdot d_i \end{aligned} xk=x2 x1 x0+α0⋅d0+α1⋅d1+⋯+αk−1⋅dk−1=x0+i=0∑k−1αi⋅di
如果 α 0 , α 1 , ⋯ , α k − 1 \alpha_0,\alpha_1,\cdots,\alpha_{k-1} α0,α1,⋯,αk−1均视作各迭代步骤中的变量,并且 x 0 , d i ( i = 0 , 1 , ⋯ , k − 1 ) x_0,d_{i}(i=0,1,\cdots,k-1) x0,di(i=0,1,⋯,k−1)均是已知项,从而可以将 f ( x k ) f(x_k) f(xk)表示为仅关于 α 0 , α 1 , ⋯ , α k − 1 \alpha_0,\alpha_1,\cdots,\alpha_{k-1} α0,α1,⋯,αk−1的函数 ϕ ( α 0 , α 1 , ⋯ , α k − 1 ) \phi(\alpha_0,\alpha_1,\cdots,\alpha_{k-1}) ϕ(α0,α1,⋯,αk−1):
f ( x k ) = ϕ ( α 0 , α 1 , ⋯ , α k − 1 ) = 1 2 ( x 0 + ∑ i = 0 k − 1 α i ⋅ d i ) T Q ( x 0 + ∑ i = 0 k − 1 α i ⋅ d i ) + C T ( x 0 + ∑ i = 0 k − 1 α i ⋅ d i ) \begin{aligned} f(x_k) & = \phi(\alpha_0,\alpha_1,\cdots,\alpha_{k-1}) \\ & = \frac{1}{2} \left(x_0 + \sum_{i=0}^{k-1} \alpha_i \cdot d_i\right)^T \mathcal Q \left(x_0 + \sum_{i=0}^{k-1} \alpha_i \cdot d_i\right) + \mathcal C^T \left(x_0 + \sum_{i=0}^{k-1} \alpha_i \cdot d_i\right) \end{aligned} f(xk)=ϕ(α0,α1,⋯,αk−1)=21(x0+i=0∑k−1αi⋅di)TQ(x0+i=0∑k−1αi⋅di)+CT(x0+i=0∑k−1αi⋅di) - 由于
x
k
x_k
xk是
X
k
\mathcal X_k
Xk内的最小点,这意味着:
x
k
x_k
xk在迭代过程中选择的步长:
a
1
,
a
2
,
⋯
,
a
k
−
1
a_1,a_2,\cdots,a_{k-1}
a1,a2,⋯,ak−1;这些步长同样构成了
ϕ
(
α
0
,
α
1
,
⋯
,
α
k
−
1
)
\phi(\alpha_0,\alpha_1,\cdots,\alpha_{k-1})
ϕ(α0,α1,⋯,αk−1)的最小解:
两个事件是等价的~
x k = x 0 + ∑ i = 0 k − 1 a i ⋅ d i ⇒ { x k = arg min { 1 2 x T Q x + C T x ∣ x ∈ X k } ( a 0 , a 2 , ⋯ , a k − 1 ) = arg min α 0 , ⋯ , α k − 1 ϕ ( α 0 , α 1 , ⋯ , α k − 1 ) \begin{aligned} & x_k = x_0 + \sum_{i=0}^{k-1} a_i \cdot d_i \Rightarrow \begin{cases} \begin{aligned} x_k = \mathop{\arg\min} \left\{\frac{1}{2} x^T \mathcal Q x + \mathcal C^T x \mid x \in \mathcal X_k\right\} \end{aligned} \\ \quad \\ (a_0,a_2,\cdots,a_{k-1}) = \mathop{\arg\min}\limits_{\alpha_0,\cdots,\alpha_{k-1}} \phi(\alpha_0,\alpha_1,\cdots,\alpha_{k-1}) \end{cases} \end{aligned} xk=x0+i=0∑k−1ai⋅di⇒⎩ ⎨ ⎧xk=argmin{21xTQx+CTx∣x∈Xk}(a0,a2,⋯,ak−1)=α0,⋯,αk−1argminϕ(α0,α1,⋯,αk−1)
如何验证上述式子成立 ? ? ?即证:
如果将变量视作一个向量:Λ = ( α 0 , ⋯ , α k − 1 ) T \Lambda = (\alpha_0,\cdots,\alpha_{k-1})^T Λ=(α0,⋯,αk−1)T,关于最优解向量A = ( a 0 , ⋯ , a k − 1 ) T \mathcal A = (a_0,\cdots,a_{k-1})^T A=(a0,⋯,ak−1)T的梯度∇ ϕ ( Λ ) ∣ Λ = A = 0 \nabla \phi(\Lambda)\mid_{\Lambda = \mathcal A} = 0 ∇ϕ(Λ)∣Λ=A=0向量;即对应各分量的偏导数均为0 0 0。
∂ ϕ ( α 0 , ⋯ , α k − 1 ) ∂ α i ∣ α i = a i = 0 i = 0 , 1 , 2 , ⋯ , k − 1 \frac{\partial \phi(\alpha_0,\cdots,\alpha_{k-1})}{\partial \alpha_i} \mid_{\alpha_i = a_i} = 0 \quad i=0,1,2,\cdots,k-1 ∂αi∂ϕ(α0,⋯,αk−1)∣αi=ai=0i=0,1,2,⋯,k−1
计算 ∂ ϕ ( α 0 , ⋯ , α k − 1 ) ∂ α i \begin{aligned}\frac{\partial \phi(\alpha_0,\cdots,\alpha_{k-1})}{\partial \alpha_i}\end{aligned} ∂αi∂ϕ(α0,⋯,αk−1):
注意复合函数求导~并且α 0 , ⋯ , α i − 1 , α i + 1 , ⋯ , α k − 1 \alpha_0,\cdots,\alpha_{i-1},\alpha_{i+1},\cdots,\alpha_{k-1} α0,⋯,αi−1,αi+1,⋯,αk−1均视作常数。
∂ ϕ ( α 0 , ⋯ , α k − 1 ) ∂ α i = 2 ⋅ 1 2 ⋅ [ Q ( x 0 + ∑ i = 0 k − 1 α i ⋅ d i ⏟ x k ) + C ] T d i = ( Q ⋅ x k + C ) T d i = [ ∇ f ( x k ) ] T d i = 0 \begin{aligned} \frac{\partial \phi(\alpha_0,\cdots,\alpha_{k-1})}{\partial \alpha_i} & = 2 \cdot \frac{1}{2} \cdot \left[\mathcal Q \left(\underbrace{x_0 + \sum_{i=0}^{k-1} \alpha_i \cdot d_i}_{x_k}\right) + \mathcal C\right]^T d_i \\ & = (\mathcal Q \cdot x_k + \mathcal C)^T d_i \\ & = [\nabla f(x_k)]^T d_i \\ & = 0 \end{aligned} ∂αi∂ϕ(α0,⋯,αk−1)=2⋅21⋅ Q xk x0+i=0∑k−1αi⋅di +C Tdi=(Q⋅xk+C)Tdi=[∇f(xk)]Tdi=0
因而 i = 0 , 1 , ⋯ , k − 1 i=0,1,\cdots,k-1 i=0,1,⋯,k−1均满足上述条件,得证。同理,当 k = n k=n k=n时,可以在完整的特征空间中找到最小解。
Reference
\text{Reference}
Reference:
最优化理论与方法-第七讲-无约束优化问题(三)