1. 树的概念

树是一种非线性的数据结构,它是由 n (n >= 0)个有限结点组成一个具有层次关系的.

把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的.

2. 树的结构

• 有一个特殊的结点,称为根节点,根节点没有前驱节点.
• 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1,T2,…Tm,其中每一个集合本身又是一棵树,并且称为根的子树
• 树是递归定义的.

注意:树形结构中,子树之间不能有交集,否则就不是树形结构,是图结构了.

---

下面就是一个平平无奇的树

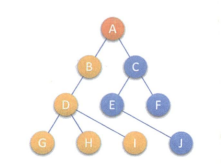
子树 T1 和子树 T2 是根节点 A 的子树,同时 D,G,H,J 组成的树也是以 B 为根节点的子树,所以说树是递归定义的.

---

对于树的定义还需要强调两点:

• n > 0 时根节点是唯一的,不可能存在多个根节点
• m > 0 时,子树的个数没有限制,但是它们一定是不相交的.

3. 树的相关概念

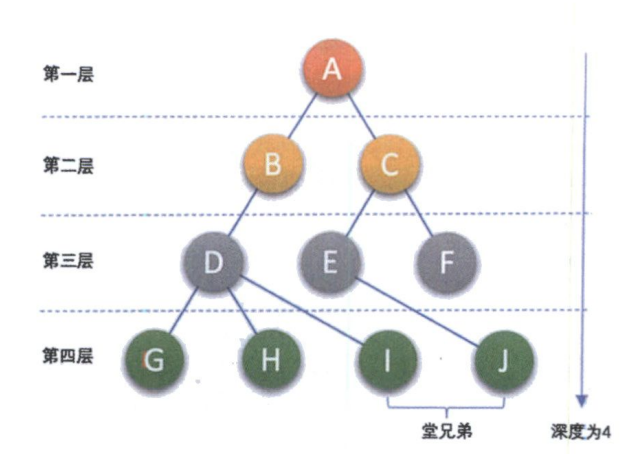
结点的度:一个结点含有子树的个数称为该结点的度; 如上图,A的为 2 ,D的为 3
叶结点或终端结点:度为 0 的结点称为叶结点; 如上图, G, H, I, J, F为叶节点
非终端结点或分支结点:度不为 0 的结点; 如上图, A, B, C, D, E为分支结点
双亲结点或父节点:若一个结点含有子节点,则这个结点称为其子节点的父节点; 如上图,A 为 B 的父节点
孩子结点或子节点:一个结点含有的子树的根节点称为该结点的子节点; 如上图,E 是 C 的孩子结点
兄弟结点:具有相同父节点的结点互称为兄弟结点;如上图,G, H, I互称为兄弟结点
树的度:一棵树中,最大的结点的度称为树的度如上图,树的度为 3
结点的层次:从根开始定义起, 根为第1层,根的子节点为第2层,以此类推
树的高度或深度:树中结点的最大层次如上图,该树的高度为4
堂兄弟结点:双亲在同一层的结点互为堂兄弟如上图, I, J互为堂兄弟结点
结点的祖先:从根到该结点所经分支上的所有节点如上图,A 是所有结点的祖先
子孙:以某结点为根的子树中任一节点都称为该节点的子孙如上图:所有结点都是 A 的子孙
森林:由 m (m > 0) 棵互不相交的树的集合称为森林

4. 树的表示

以前学单链表的时候就有一个指针,双链表有两个指针,但是树有几个指针就不确定了,因为树没有规定每个结点有多少孩子.
有三种方式来表示

孩子表示法

说明了树的度为N,使用顺序表表示

每个结点有多个指针域,其中每个指针指向一棵子树的根节点

#define N 3     //假设树的度为N

struct TreeNode
{
    int val;
    struct TreeNode* child[N];  //指针数组
};  

但是这样的表示也有缺陷,就是需要知道树的度,而且很有可能造成空间的浪费

双亲表示法

每个结点中,附设一个指示器指示其双亲结点在数组中的位置

struct TreeNode
{
    int val;
    int parent;
}

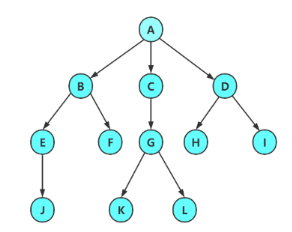
虽然找到该结点的双亲结点时间复杂度为$O(1)$, 但是要找到该结点的子节点却仍然需要遍历整个树才可以找到,显然这个结构也有缺陷

孩子兄弟表示法

任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的.因此,我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟.

struct TreeNode
{
    int val;
    struct TreeNode* firstchild;
    struct TreeNode* nextbrother;
}

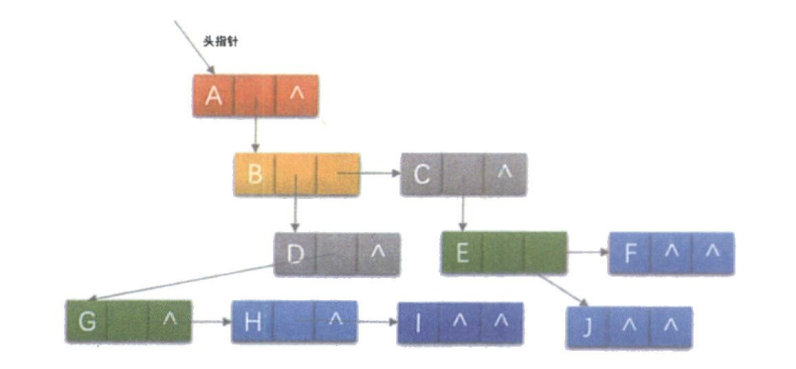
这样可以说是最优的表示法了
如果我们想要得到某个结点的所有孩子,下面的代码就可以了.

struct TreeNode* Anode;
struct TreeNode* child = Anode->firstchild;

while (child)
{
    printf("%d ", child->val);
    child = child->nextbrother;
}

这样确实做到了最大节省空间,同时,这也是一个二叉树,它的逻辑结构适合很多操作,是一个很优秀的逻辑结构.

5. 树在实际中的应用

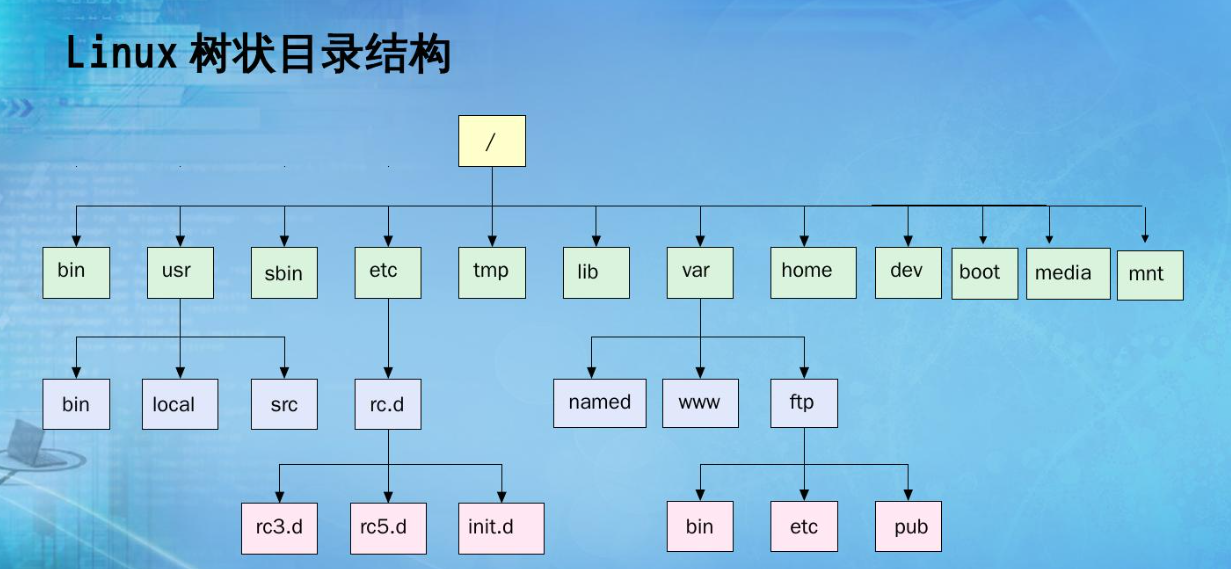
文件系统的目录树结构、网络拓扑，最短路径问题，搜索引擎、思维导图等
了最大节省空间,同时,这也是一个二叉树,它的逻辑结构适合很多操作,是一个很优秀的逻辑结构.

5. 树在实际中的应用

文件系统的目录树结构、网络拓扑，最短路径问题，搜索引擎、思维导图等