目录

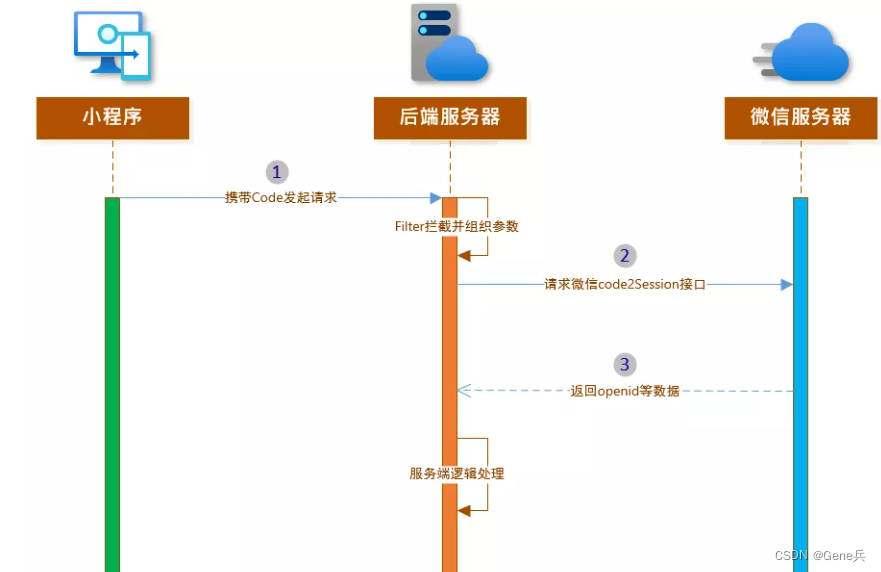
第17章 KNN算法（有监督学习算法，放在此位置是为了与下一章的K-means做对比）

17.1 KNN算法原理

17.2 KNN中的K

第18章 K-means——最简单的聚类算法

18.1 K-means算法步骤

18.2 K-means算法具体细节

18.3 启发式算法

18.4 K-means算法的局限性

18.5 K-means算法代码实现

18.6 KNN实例

---

第17章 KNN算法（有监督学习算法，放在此位置是为了与下一章的K-means做对比）

17.1 KNN算法原理

KNN算法的基本思想是:

• 训练数据包括样本的特征向量(x)和标签(y)
• K是一个常数，由用户来定义
• 一个没有标签的样本进入算法后，首先找到与它距离最近的K个样本，然后用它的K个最近邻的标签来确定它的标签。

KNN 算法的步骤如下。

• 算距离:给定未知对象，计算它与训练集中的每个样本的距离。在特征变量连续的情况下，将欧氏距离作为距离度量;若特征是离散的，也可以用重叠度量或者其他指标作为距离，这要结合具体情况分析。
• 找近邻:找到与未知对象距离最近的K个训练样本。
• 做分类/回归:将在这K个近邻中出现次数最多的类别作为未知对象的预测类别(多数表决法)，或者是取K个近邻的目标值平均数，作为未知对象的预测结果。

多数表决法有个问题，如果训练样本的类别分布不均衡，那么出现频率较多的样本将会主导预测结果。这一问题的解决办法有多种，其中常见的一种是:不再简单计算K个近邻中的多数。而是同时考虑K个近邻的距离，K个近邻中每一个样本的类别(或目标值)都以距离的倒数为权值，最后求全体加权结果。

---

17.2 KNN中的K

在KNN算法中，假设训练样本一共有m个，当一个待预测样本进来的时候，它要与每一个训练样本进行距离计算，然后从中选出K个最近的邻居，根据这 K个近邻标签确定自己的预测值。

此处的K是一个正整数。若K=1，则该对象的预测值直接由最近的一个样本确定。若 K=m，则整个训练集共同确定待测样本。

通常K>1，但也不会太大，是一个“较小”的正整数。具体取何值最佳，则取决于训练数据和算法目标。

在一般情况下，K值越大，受噪声的影响越小;但K值越大，也越容易模糊类别之间的界限。

比如下图所示的这个例子，用 KNN 做分类，黑色为A类，蓝色为B 类，五角星的是待测样本

当我们取K=3时，根据多数选举法，预测结果为 B;但当K=6时，依然是根据多数选举法，预测结果就成了A。可见，K的取值大小直接影响着算法的结果。

---

第18章 K-means——最简单的聚类算法

18.1 K-means算法步骤

算法步骤

• Step0:用户确定K值，并将n个样本投射为特征空间中的n个点(K≤n)。
• Step1:算法在这n个点中随机选取K个点，作为初始的簇核心。
• Step2:分别计算每个样本点到K个簇核心的距离(一般取欧氏距离或余弦距离)，找到离该点最近的簇核心，将它归到对应的簇。
• Step 3:所有点都归属到簇之后，n个点就分为了 K个簇。之后重新计算每个簇的重心，将其定为新的簇核心。
• Step4:反复迭代Step2~Step3，直到簇核心不再移动。

---

18.2 K-means算法具体细节

目标

有n个样本x1，x2，…，xn，每个都是d维实向量，K-means聚类的目标是将它们分为K簇(K≤n)，这些簇表示为S={S1，S2,…,Sk}。

K-means算法的目标是簇内平方和最小:

分配

更新

对于该簇中的样本求均值即可

---

18.3 启发式算法

启发式算法是一种基于直观或经验构造的算法。相对于最优化算法要求得待解决问题的最优解，启发式算法力求在可接受的花费(消耗的时间和空间)下，给出待解决问题的一个可行解，该可行解与最优解的偏离程度一般不能被预计。启发式算法常能发现不错的解，但也没办法证明它不会得到较坏的解，它通常可在合理时间内解出答案，但也没办法知道它是否每次都能够以这样的速度求解。

虽然有种种不确定性，且其性能无法得到严格的数学证明，但启发式算法直观、简单、易于实现。在某些特殊情况下，启发式算法会得到很坏的答案或效率极差，不过造成那些特殊情况的数据组合也许永远不会在现实世界出现。因此现实世界中常用启发式算法来解决问题。

最常见的用于实现 K-means 的启发式算法为 Lloyd’s 算法。Lloyd’s算法是一种很高效的算法，通常它的时间复杂度是O(nkdi)，其中n为样本数，k为簇数，d为样本维度数，而i为从开始到收敛的迭代次数。

如果样本数据本身就有一定的聚类结构，那么收敛所需的迭代次数通常是很少的，而且一般前几十次迭代之后，每次迭代的改进就很小了。

因此，在实践中，Lloyd’s算法往往被认为是线性复杂度的算法，虽然在最糟糕的情况下时间复杂度是超多项式的。

目前，Lloyd’s 算法是 K-means 聚类的标准方法。当然，每一次迭代它都要计算每个簇中各个样本到簇核心的距离,这是很耗费算力的。不过在大多数情况下，经过头几轮的迭代，各个簇就相对稳定了，大多数样本不会再改变簇的归属，可以利用缓存等方法来简化后续的计算。

---

18.4 K-means算法的局限性

K-means 简单直观，有了启发式算法后，计算复杂度也可以接受，但存在以下问题。

• K值对最终结果的影响很大，而它却必须预先给定。给定合适的K值需要先验知识很难凭空估计，否则可能导致效果很差。
• 初始簇核心很重要，几乎可以说是算法敏感的，偏偏它们一般是被随机选定的。一旦选择得不合适，就只能得到局部最优解。当然，这也是由K-means 算法本身的局部最优性决定的。
• K-means 存在的问题造成了K-means的应用有限，使得它并不适合所有的数据。例如，对于非球形簇，或者多个簇之间尺寸和密度相差较大的情况，K-means 就处理不好了。

---

18.5 K-means算法代码实现

训练样本是10个人的身高体重数据

from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt

X = np.array([[185.4, 72.6], [155.0, 54.4], [170.2, 99.9], [172.2, 97.3], [157.5, 59.0], [190.5, 81.6], [188.0, 77.1], [167.6, 97.3], [172.7, 93.3], [154.9, 59.0]])

kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
y_kmeans = kmeans.predict(X)
centroids = kmeans.cluster_centers_

plt.scatter(X[:, 0], X[:, 1], s=50);
plt.yticks(())
plt.show()

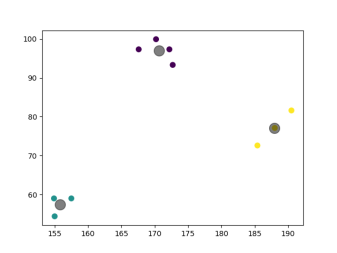
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
plt.scatter(centroids[:, 0], centroids[:, 1], c='black', s=200, alpha=0.5);
plt.show()

 运行结果为

我们预测下两个新的样本

print(kmeans.predict([[170.0,60],[155.0,50]]))

（注意，原书这里代码有点错误，应该是kmeans，而非K-means）

输出结果为

[1 1]

---

18.6 KNN实例

我们没必要手动打标签，因为我们可以利用上一节K-means的结果作为KNN的标签

from sklearn.neighbors import KNeighborsClassifier
X = [[185.4, 72.6],
[155.0, 54.4],
[170.2, 99.9],
[172.2, 97.3],
[157.5, 59.0],
[190.5, 81.6],
[188.0, 77.1],
[167.6, 97.3],
[172.7, 93.3],
[154.9, 59.0]]
y = [0, 1, 2, 2, 1, 0, 0, 2, 2, 1]
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X, y)


print(neigh.predict([[170.0, 60], [155.0, 50]]))

运行结果

[1 1]