前言

比赛结束了不知道大家情况如何，就我个人而言的话，由于工作任务比较繁重仅完成了对D题和E题的思路解答和建模，还是比较遗憾的。一个人要完成多题的建模和分析确实不是一件容易的事情，当然我向大家做出承诺历年的建模比赛我都会写出详解和建模过程，只要大家需要我的帮助，我会尽我最大的能力完成。本次大赛中个人认为E题是一道比较好上手的题目，题意简洁，建模思路清晰明了。但是由于是时间序列数据，数据处理方面可能会比较麻烦，虽然建模思路比较清晰，但是时序预测分析算法还是有一定难度的，细节很多。相对于D题来说，对建模手能力要求要高。

对于时间序列数据本人有过较多行业内分析经验，故做此题还是比较轻松的，时间序列数据在领域行业方面是要经常打交道的，以后想要从事数据分析或者数据挖掘应该要对此类数据建模过程熟悉。对此方面感兴趣的同学或是想要学习这方面建模的知识推荐订阅博主的专栏，关于时序数据处理和建模我已经整理好了十来篇以及关于此类模型建模运用的案例：

博主专注建模四年，参与过大大小小数十来次数学建模，理解各类模型原理以及每种模型的建模流程和各类题目分析方法。此专栏的目的就是为了让零基础快速使用各类数学模型、机器学习和深度学习以及代码，每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛，每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码。希望有需求的小伙伴不要错过笔者精心打造的专栏。

一、问题重述

赛题背景

研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变化和人民生活的影响，以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾等方面都具有重要的理论指导意义。

建模需求

根据该水文站水沙通量的变化规律，预测分析该水文站未来两年水沙通量的变化趋势。

建模分析

本题最重要的关键在于第三问，第一问和第二问我都有源码详解解答，大部分是数据处理和统计的工作，并没有深度的建模需求，但是第三问就很明确的给出了需求：需要建立时序预测模型来分析预测该水文站未来两年水沙通量的变化趋势。那么经过了问题一和问题二的铺垫，我们对数据也有了较为清晰的认识，也将数据转化为我们想要的格式，如果对第一问和第二问有疑问的同学去看我之前的文章：

(源码版)2023 年高教社杯全国大学生数学建模竞赛-E 题黄河水沙监测题一数据分析详解+Python代码

数据处理完的数据格式为：

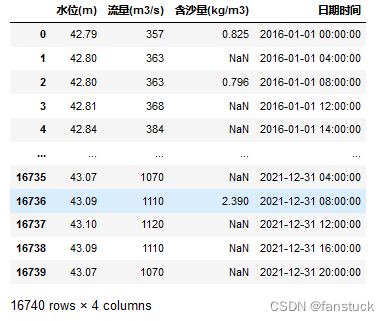
这里数据需要注意一下，一天仅记录一次数据且记录时间不是固定的，不过由于时间预测范围是两年，因此建模过程中我们设定的时间维度最好大一点，也就是采取维度为日最好，不然如果设置为小时的话数据十分稀疏，而且填充数据误差也太大了，因此直接默认该天数据以一次小时记录为准即可，题意也是让你这么做的。最终处理结果：

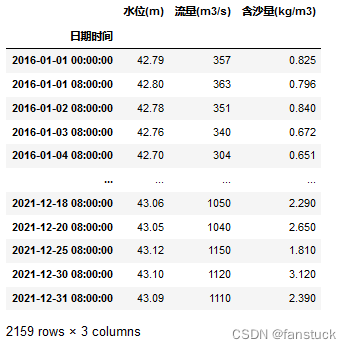
数据预览

进行建模之前我们最好还是预览一下数据的变化，辅助我们判断：

水位:

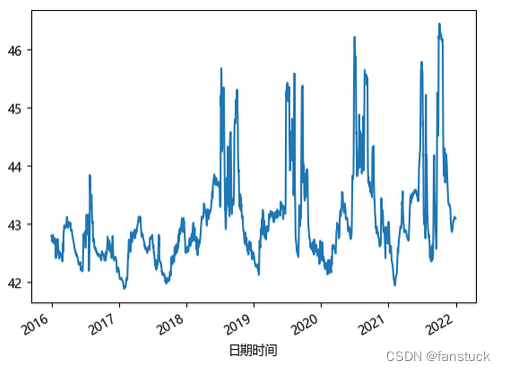
水流量：

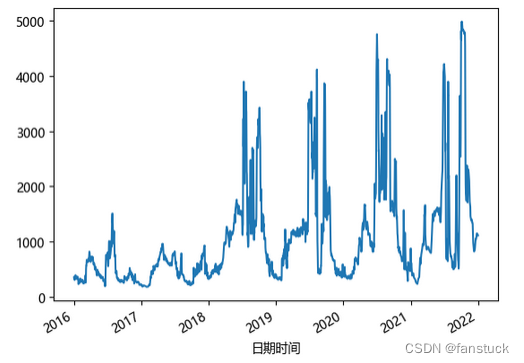
含沙量：

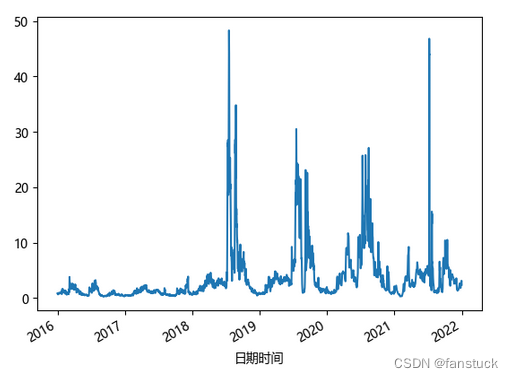
很明显该数据呈现一定的周期性波动，且在年终的时候数据起伏要比其他时间段多很多。描述这类序列的模型称作季节时间序列模型(seasonal ARIMA model),用SARIMA表示。季节时间序列模型也称作乘积季节模型(Multiplicative seasonal model)。那么我们现在可以开始建模了。

SARIMA模型建模

SARIMA（Seasonal Autoregressive Integrated Moving Average）是一种基于 ARIMA 模型的季节时间序列预测模型。ARIMA 模型是一种广泛应用于时间序列预测的经典模型，它考虑了时间序列的趋势性和周期性。SARIMA 模型在 ARIMA 模型的基础上增加了季节性，因此可以更好地应对具有季节性变化的时间序列数据。
SARIMA 模型通常包含以下几个参数：

季节周期 (Seasonal period)：时间序列数据呈现季节性变化的周期，例如一年、一周、一天等。
差分次数 (Order of differencing)：对时间序列数据进行差分的次数，以消除数据的非平稳性。
自回归项 (Autoregressive terms)：用于建立时间序列与其过去值的关系，表示时间序列数据的趋势性。
移动平均项 (Moving average terms)：用于建立时间序列的随机波动性与过去的误差的关系，表示时间序列数据的随机性。

SARIMA 模型可以用来预测具有季节性变化的时间序列数据，例如销售额、气温、股票价格等。它需要基于历史数据来拟合模型，然后使用模型来预测未来一段时间内的数据。在使用 SARIMA 模型时，需要选择合适的参数和模型结构，并进行模型诊断和调优，以获得更准确的预测结果。

数据填充

这里需要注意的是，从2016年1月1日开始计算到2021年12月31天总共有2192天才对，而数据仅有2159条，一天内有重复数据且纯在天数空缺没有记录，我们需要进行数据填充。

先将数据时间范围补齐：

# 创建完整日期范围的日期索引
date_range = pd.date_range(start='2016-01-01', end='2021-12-31', freq='D')
# 创建包含完整日期范围的 DataFrame
date_df = pd.DataFrame(index=date_range)
# 将原始数据与日期索引合并
merged_df = date_df.merge(df_with_sediment, left_index=True, right_on='日期时间', how='left')
# 将缺失值填充为特定的值（这里是NaN）
merged_df['水位(m)'].fillna('NaN', inplace=True)
merged_df=merged_df.set_index(merged_df['日期时间'])
# 删除原始的日期时间列
merged_df.drop(columns=['日期时间'], inplace=True)
merged_df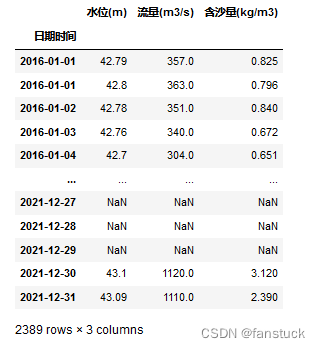

此时保留相同日期的第一个时间索引的数据：

进行指数平滑法填充：

merged_df['水位(m)'].fillna(merged_df['水位(m)'].ewm(span=3).mean(), inplace=True)
merged_df['流量(m3/s)'].fillna(merged_df['流量(m3/s)'].ewm(span=3).mean(), inplace=True)
merged_df['含沙量(kg/m3) '].fillna(merged_df['含沙量(kg/m3) '].ewm(span=3).mean(), inplace=True)
merged_df

数据填充完成之后可以开始进行季节性分析了。

季节性分析

可以使用seasonal_decompose()进行分析，将时间序列分解成长期趋势项(Trend)、季节性周期项(Seansonal)和残差项(Resid)这三部分。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
from matplotlib.pylab import rcParams
import pmdarima as pm
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf  # 画图定阶
from statsmodels.tsa.stattools import adfuller                 # ADF检验
from statsmodels.stats.diagnostic import acorr_ljungbox        # 白噪声检验
import warnings
import itertools
warnings.filterwarnings("ignore")  # 选择过滤警告
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
from statsmodels.tsa.seasonal import seasonal_decompose
# 分解数据查看季节性   freq为周期
# 推断频率参数
ts_decomposition = seasonal_decompose(merged_df['水位(m)'],  period=52)
ts_decomposition.plot()
plt.show()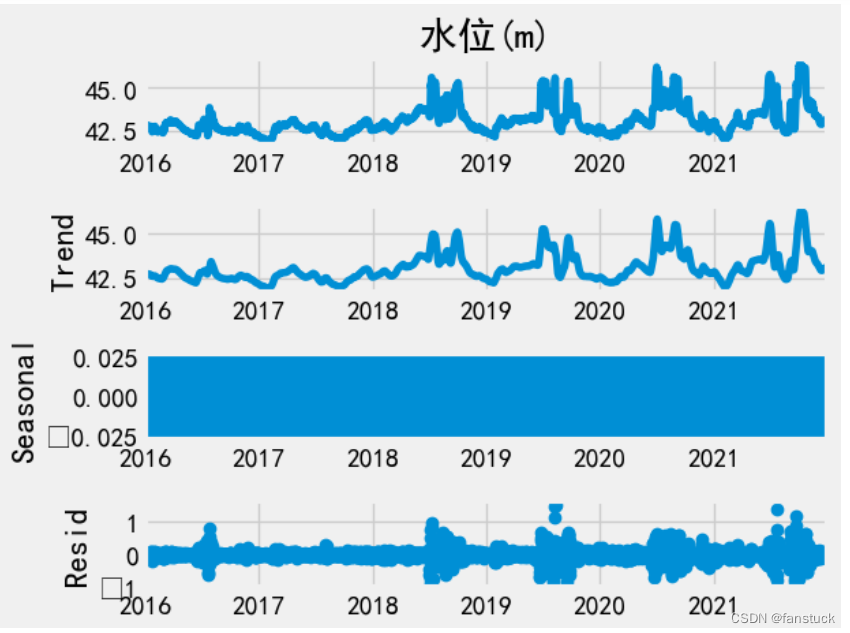

方框为负号。

ADF检验

ARIMA模型要求时间序列是平稳的。所谓平稳性，其基本思想是：决定过程特性的统计规律不随着时间的变化而变化。由平稳性的定义：对于一切t,s, $Y_{t}$ 和 $Y_{s}$ 的协方差对于时间的依赖之和时间间隔 $|t-s|$ 有关，而与实际的时刻t和s无关。因此，平稳过程可以简化符号，其中 $Cov$ 为自协方差函数， $Corr$ 为自相关函数，记为：

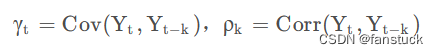
关于严宽平稳我之前写自回归模型(AR)已经写的很清楚了。如果通过时间序列图来用肉眼观看的话可能会存在一些主观性。ADF检验（又称单位根检验）是一种比较常用的严格的统计检验方法。

ADF检验主要是通过判断时间序列中是否含有单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。

from statsmodels.tsa.stattools import adfuller                 # ADF检验
 
def stableCheck(timeseries):
    # 移动60期的均值和方差
    rol_mean = timeseries.rolling(window=60).mean()
    rol_std = timeseries.rolling(window=60).std()
    # 绘图
    fig = plt.figure(figsize=(12, 8))
    orig = plt.plot(timeseries, color='blue', label='Original')
    mean = plt.plot(rol_mean, color='red', label='Rolling Mean')
    std = plt.plot(rol_std, color='black', label='Rolling Std')
    plt.legend(loc='best')
    plt.title('Rolling Mean & Standard Deviation')
    plt.show()
    # 进行ADF检验
    print('Results of Dickey-Fuller Test:')
    dftest = adfuller(timeseries, autolag='AIC')
    # 对检验结果进行语义描述
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic', 'p-value', '#Lags Used', 'Number of Observations Used'])
    for key, value in dftest[4].items():
        dfoutput['Critical Value (%s)' % key] = value
    print('ADF检验结果:')
    print(dfoutput)

Results of Dickey-Fuller Test:
ADF检验结果:
Test Statistic                   -5.503970
p-value                           0.000002
#Lags Used                        7.000000
Number of Observations Used    2184.000000
Critical Value (1%)              -3.433348
Critical Value (5%)              -2.862864
Critical Value (10%)             -2.567475

根据所提供的ADF检验结果，可以得到以下结论：

Test Statistic（测试统计量）: -5.503970

测试统计量是ADF检验的一个关键输出。它比较了实际数据与随机漫步（即没有趋势）之间的差异。这个值越低，表示数据中可能存在趋势。

p-value（p值）: 0.000002

p值是假设检验的一个关键输出，它表示在原假设为真的情况下，观察到测试统计量或更极端情况的概率。在这里，p值非常接近于零，远小于通常使用的显著性水平（例如0.05），这表明我们可以拒绝原假设。

#Lags Used（使用的滞后阶数）: 7

这是在单位根检验中使用的滞后阶数。它可以帮助确定是否存在自相关性。

Number of Observations Used（使用的观测样本数）: 2184

这表示在检验中使用的观测样本数。

Critical Values（临界值）:

临界值是用于比较测试统计量的阈值。在不同的显著性水平下（1%，5%，10%等），它们确定了拒绝原假设的临界值。

根据p值小于通常的显著性水平（例如0.05），我们可以拒绝原假设，即时间序列数据是稳定的。因此，根据此ADF检验的结果，可以得出结论：该时间序列数据是稳定的，没有单位根，具有趋势性。

白噪声检验

如果平稳序列是非白噪声序列，那么说明它不是由随机噪声组成的。这意味着序列中存在一些内在的结构或模式，这些结构或模式可以被进一步分析和建模，以便进行预测或其他目的。我们可以通过Ljung-Box检验，是时间序列分析中检验序列自相关性的方法

def whiteNoiseCheck(data):
    result = acorr_ljungbox(data, lags=1)
    temp = result.iloc[:,1].values[0]
    #print(result.iloc[:,1].values[0])
    print('白噪声检验结果：', result)
    # 如果temp小于0.05，则可以以95%的概率拒绝原假设，认为该序列为非白噪声序列；否则，为白噪声序列，认为没有分析意义
    print(temp)
    return result
ifwhiteNoise = whiteNoiseCheck(df_evel_timese_diff2)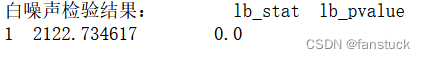

LB统计量用于评估序列中是否存在自相关性，p-value则用于判断序列是否为白噪声。一般来说，如果序列是白噪声，那么LB统计量的值会接近0，p-value会很大，说明序列中不存在自相关性。但是如果p-value小于显著性水平（通常是0.05），那么就可以拒绝原假设，即序列不是白噪声。在这个检验结果中，LB统计量为2122，p-value接近0，p-value远小于0.05，因此可以拒绝原假设，即序列不是白噪声。

模型拟合

拟合SARIMA模型需要确定其参数。SARIMA模型有三个重要的参数：p、d和q，分别代表自回归阶数、差分阶数和移动平均阶数；另外还有季节性参数P、D和Q，分别代表季节性自回归阶数、季节性差分阶数和季节性移动平均阶数。根据经验和统计方法，可以通过观察样本自相关函数ACF和偏自相关函数PACF，选取最佳的p、d、q和P、D、Q参数，使得残差序列的自相关函数和偏自相关函数均值为0。

时间序列定阶

from matplotlib.ticker import MultipleLocator
def draw_acf(data):
    # 利用ACF判断模型阶数
    plot_acf(data)
    plt.title("序列自相关图(ACF)")
    plt.show()
 
def draw_pacf(data):
    # 利用PACF判断模型阶数
    plot_pacf(data)
    plt.title("序列偏自相关图(PACF)")
    plt.show()
    
def draw_acf_pacf(data):
    f = plt.figure(facecolor='white')
    # 构建第一个图
    ax1 = f.add_subplot(211)
    # 把x轴的刻度间隔设置为1，并存在变量里
    x_major_locator = MultipleLocator(1)
    plot_acf(data,  ax=ax1)
    # 构建第二个图
    ax2 = f.add_subplot(212)
    plot_pacf(data, ax=ax2)
    plt.subplots_adjust(hspace=0.5)
    # 把x轴的主刻度设置为1的倍数
    ax1.xaxis.set_major_locator(x_major_locator)
    ax2.xaxis.set_major_locator(x_major_locator)
    plt.show()

(1)确定 $d$ 和 $D$ 的阶数：当对原序列进行了 $d$ 阶差分和 $lag$ 为 $m$ 的 $D$ 阶差分后序列为平稳序列，则可以确定 $d$ ， $D$ ， $m$ 的值。

(2)确定 $p,q$ 和 $P,Q$ 的阶数：

首先对平稳化后的时间序列绘制ACF和PACF图；
通过观察季节性 $lag$ 处的拖尾/截尾情况来确定 $P,Q$ 的值
观察短期非季节性 $lag$ 处的拖尾/截尾情况来确定 $p,q$ 的值

之前已经在步骤三处确定了 $d,D,m$ 。对于剩下的参数，将依据如下的ACF和PACF图确定。下图的横坐标 $lag$ 是以月份为单位。

非季节性部分：

对于 $p$ ，在 $lag=1$ 后， $ACF$ 图拖尾， $PACF$ 图截尾。同样地，对于 $q$ ，在 $lag=1$ 后， $ACF$ 图截尾， $PACF$ 图截尾。同样地，对于 $q$ ，在 $lag=1$ ,ACF图截尾，PACF图拖尾。

季节性部分：

$P$ ， $Q$ 的确定和非季节性一样，不过需要记得滞后的间隔为60。

AR模型：自相关系数拖尾，偏自相关系数截尾；
MA模型：自相关系数截尾，偏自相关函数拖尾；
ARMA模型：自相关函数和偏自相关函数均拖尾。

pmdarima.auto_arima()方法可以帮助我们自动确定 $ARIMA(p,d,q)(P,D,Q)_{m}$ 的参数,直接输入数据，设置auto_arima()中的参数则可。

模型训练

import pmdarima as pm
split_point = int(len(time_series) * 0.85)
# 确定训练集/测试集
data_train, data_test = time_series[0:split_point], time_series[split_point:len(time_series)]
# 使用训练集的数据来拟合模型
built_arimamodel = pm.auto_arima(data_train,
                                 start_p=0,   # p最小值
                                 start_q=0,   # q最小值
                                 test='adf',  # ADF检验确认差分阶数d
                                 max_p=5,     # p最大值
                                 max_q=5,     # q最大值
                                 m=12,        # 季节性周期长度，当m=1时则不考虑季节性
                                 d=None,      # 通过函数来计算d
                                 seasonal=True, start_P=0, D=1, trace=True,
                                 error_action='ignore', suppress_warnings=True,
                                 stepwise=False  # stepwise为False则不进行完全组合遍历
                                 )
print(built_arimamodel.summary())

这样一来我们就得到了最佳参数，auto_arima直接建立好了模型，当然如果想要根据ADF图片自己选择参数也可以：

from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error


# 拟合ARIMA模型
model_water = ARIMA(merged_df['水位(m)'], order=(2, 0, 1))
results_water = model_water.fit()

# 评估模型
mse_water = mean_squared_error(merged_df['水位(m)'], results_water.fittedvalues)

print(f'Mean Squared Error (Water Level): {mse_water}')

Mean Squared Error (Water Level): 0.02088585362915174

均方误差才0.02，这个结果已经是比较满意了接下里我们可以来试试预测未来两年的水位了：

# 定义要预测的时间范围
forecast_range = pd.date_range(start='2021-12-31', periods=730, freq='D')  # 预测未来两年，共730天

# 使用模型进行预测
forecast = results_water.get_forecast(steps=730)