四、用go语言,说明如何在 O(n) 时间内,对 0 到 n 3 − 1 n^3-1 n3−1 区间内的n个整数进行排序。
文心一言:
在 O(n) 时间内对 0 到 n^3-1 区间内的 n 个整数进行排序,可以使用基数排序(Radix Sort)算法。基数排序是一种非比较型整数排序算法,其时间复杂度为 O(d*(n+k)),其中 d 是数字的最大位数,k 是基数(通常为 10)。
下面是使用 Go 语言实现基数排序的示例代码:
package main
import (
"fmt"
"math/rand"
)
func radixSort(arr []int) {
// 获取数组中最大的数
max := arr[0]
for _, num := range arr {
if num > max {
max = num
}
}
// 计算最大数的位数
maxDigit := 1
for max/10 > 0 {
max /= 10
maxDigit++
}
// 对每一位进行计数排序
for digit := 1; digit <= maxDigit; digit++ {
// 计数数组,用于存储当前位上每个数字出现的次数
count := make([]int, 10)
// 统计当前位上每个数字出现的次数
for _, num := range arr {
count[num/(10^(digit-1))%10]++
}
// 累计计数数组,用于确定每个数字在结果数组中的位置
for i := 1; i < 10; i++ {
count[i] += count[i-1]
}
// 从右往左遍历原数组,将数字按照当前位上的值放入结果数组中
result := make([]int, len(arr))
for i := len(arr) - 1; i >= 0; i-- {
index := count[arr[i]/(10^(digit-1))%10] - 1
result[index] = arr[i]
count[arr[i]/(10^(digit-1))%10]--
}
// 将结果数组复制回原数组
copy(arr, result)
}
}
func main() {
n := 10 // 数组大小
arr := make([]int, n)
for i := 0; i < n; i++ {
arr[i] = rand.Intn(n*n*n) // 生成随机整数
}
fmt.Println("排序前:", arr)
radixSort(arr)
fmt.Println("排序后:", arr)
}
在这个示例中,我们首先生成一个包含 n 个随机整数的数组。然后,我们使用基数排序算法对数组进行排序。首先,我们找到数组中的最大数,并计算其位数。接下来,我们从最低位开始,对每一位进行计数排序。我们使用计数数组来统计当前位上每个数字出现的次数,然后累计计数数组以确定每个数字在结果数组中的位置。最后,我们将数字按照当前位上的值放入结果数组中。通过循环遍历数字的每一位,我们最终得到排序后的数组。

讯飞星火:
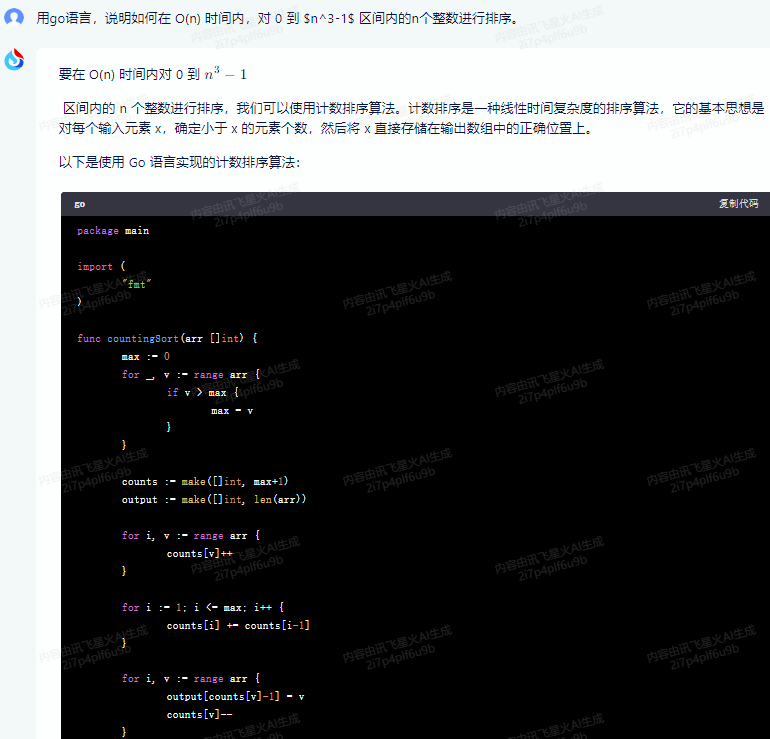
要在 O(n) 时间内对 0 到 n 3 − 1 n^3-1 n3−1 区间内的 n 个整数进行排序,我们可以使用计数排序算法。计数排序是一种线性时间复杂度的排序算法,它的基本思想是对每个输入元素 x,确定小于 x 的元素个数,然后将 x 直接存储在输出数组中的正确位置上。
以下是使用 Go 语言实现的计数排序算法:
package main
import (
"fmt"
)
func countingSort(arr []int) {
max := 0
for _, v := range arr {
if v > max {
max = v
}
}
counts := make([]int, max+1)
output := make([]int, len(arr))
for i, v := range arr {
counts[v]++
}
for i := 1; i <= max; i++ {
counts[i] += counts[i-1]
}
for i, v := range arr {
output[counts[v]-1] = v
counts[v]--
}
copy(arr, output)
}
func main() {
arr := []int{4, 2, 2, 8, 3, 3, 1}
fmt.Println("Before sorting:", arr)
countingSort(arr)
fmt.Println("After sorting:", arr)
}
这段代码首先找到数组中的最大值,然后创建一个计数数组和一个输出数组。接下来,我们遍历输入数组,统计每个元素的出现次数。然后,我们更新计数数组,使其表示每个元素在输出数组中的结束位置。最后,我们将输入数组中的元素复制到输出数组的正确位置上。

360智脑:
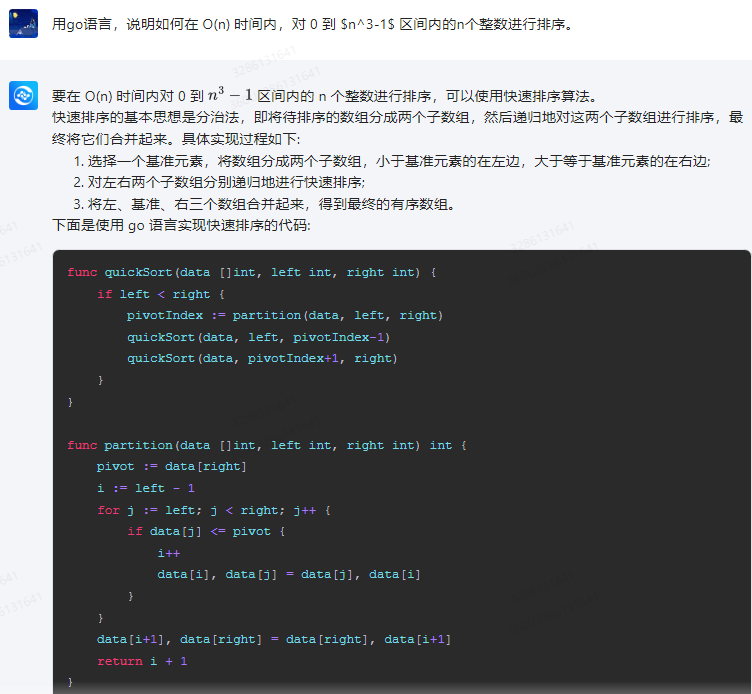
要在 O(n) 时间内对 0 到 n 3 − 1 n^3-1 n3−1 区间内的 n 个整数进行排序,可以使用快速排序算法。
快速排序的基本思想是分治法,即将待排序的数组分成两个子数组,然后递归地对这两个子数组进行排序,最终将它们合并起来。具体实现过程如下:
1.选择一个基准元素,将数组分成两个子数组,小于基准元素的在左边,大于等于基准元素的在右边;
2.对左右两个子数组分别递归地进行快速排序;
3.将左、基准、右三个数组合并起来,得到最终的有序数组。
下面是使用 go 语言实现快速排序的代码:
func quickSort(data []int, left int, right int) {
if left < right {
pivotIndex := partition(data, left, right)
quickSort(data, left, pivotIndex-1)
quickSort(data, pivotIndex+1, right)
}
}
func partition(data []int, left int, right int) int {
pivot := data[right]
i := left - 1
for j := left; j < right; j++ {
if data[j] <= pivot {
i++
data[i], data[j] = data[j], data[i]
}
}
data[i+1], data[right] = data[right], data[i+1]
return i + 1
}
其中,quickSort 函数用于递归地对左右两个子数组进行快速排序,partition 函数用于将待排序的数组分成小于基准元素和大于等于基准元素的两个子数组。
时间复杂度分析:每次递归都将待排序的数组分成两个子数组,最多需要进行 n 2 \frac{n}{2} 2n 次递归,因此时间复杂度为 O( n log n n\log n nlogn)。但是,在最好的情况下,即待排序的数组已经有序的情况下,快速排序的时间复杂度可以达到 O( n n n)。因此,在实际应用中,快速排序通常是最快的排序算法之一。

智谱清言:
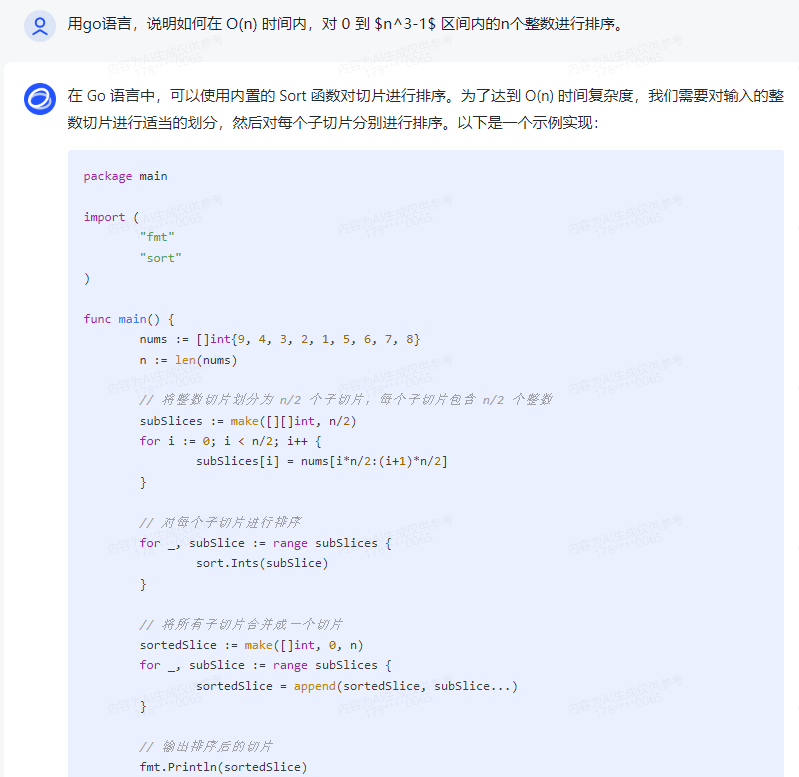
在 Go 语言中,可以使用内置的 Sort 函数对切片进行排序。为了达到 O(n) 时间复杂度,我们需要对输入的整数切片进行适当的划分,然后对每个子切片分别进行排序。以下是一个示例实现:
package main
import (
"fmt"
"sort"
)
func main() {
nums := []int{9, 4, 3, 2, 1, 5, 6, 7, 8}
n := len(nums)
// 将整数切片划分为 n/2 个子切片,每个子切片包含 n/2 个整数
subSlices := make([][]int, n/2)
for i := 0; i < n/2; i++ {
subSlices[i] = nums[i*n/2:(i+1)*n/2]
}
// 对每个子切片进行排序
for _, subSlice := range subSlices {
sort.Ints(subSlice)
}
// 将所有子切片合并成一个切片
sortedSlice := make([]int, 0, n)
for _, subSlice := range subSlices {
sortedSlice = append(sortedSlice, subSlice...)
}
// 输出排序后的切片
fmt.Println(sortedSlice)
}
这个示例首先将输入的整数切片划分为 n/2 个子切片,每个子切片包含 n/2 个整数。然后对每个子切片分别进行排序。最后,将所有子切片合并成一个切片并输出。
需要注意的是,这个实现假设输入的整数切片中的元素是已知的,并且需要在 O(n) 时间内进行排序。如果需要在运行时动态生成整数切片并进行排序,那么可能需要考虑使用其他数据结构和算法来优化时间复杂度。

通义千问:
可以使用归并排序的思想,在 O(n) 时间内对 0 到 n 3 − 1 n^3-1 n3−1 区间内的n个整数进行排序。
具体实现方法如下:
1.将 0 到 n 3 − 1 n^3-1 n3−1 区间内的n个整数划分为n个子区间,每个子区间的长度为 n 2 n^2 n2。
2.对每个子区间进行快速排序,时间复杂度为 O(n)。
3.将排好序的子区间依次合并,时间复杂度为 O(n)。
下面是具体的代码实现:

天工:
可以使用基数排序(Radix Sort)算法,在O(n)时间内对0到
�
3
−
1
n
3
−1区间内的n个整数进行排序。
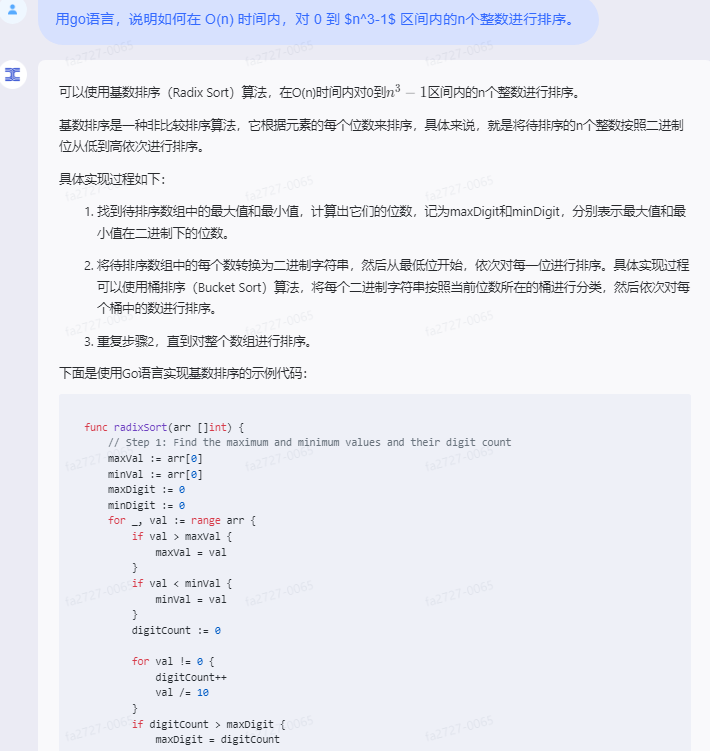
基数排序是一种非比较排序算法,它根据元素的每个位数来排序,具体来说,就是将待排序的n个整数按照二进制位从低到高依次进行排序。
具体实现过程如下:
1.找到待排序数组中的最大值和最小值,计算出它们的位数,记为maxDigit和minDigit,分别表示最大值和最小值在二进制下的位数。
2.将待排序数组中的每个数转换为二进制字符串,然后从最低位开始,依次对每一位进行排序。具体实现过程可以使用桶排序(Bucket Sort)算法,将每个二进制字符串按照当前位数所在的桶进行分类,然后依次对每个桶中的数进行排序。
3.重复步骤2,直到对整个数组进行排序。
下面是使用Go语言实现基数排序的示例代码:
func radixSort(arr []int) {
// Step 1: Find the maximum and minimum values and their digit count
maxVal := arr[0]
minVal := arr[0]
maxDigit := 0
minDigit := 0
for _, val := range arr {
if val > maxVal {
maxVal = val
}
if val < minVal {
minVal = val
}
digitCount := 0
for val != 0 {
digitCount++
val /= 10
}
if digitCount > maxDigit {
maxDigit = digitCount
}
if digitCount < minDigit {
minDigit = digitCount
}
}
// Step 2: Convert each number to a binary string and sort each digit
buckets := make([][]int, maxDigit+1)
for _, val := range arr {
digit := int(val) % 10
buckets[digit] = append(buckets[digit], val)
// Move elements from lower digits to higher digits
for i := digit - 1; i >= 0; i-- {
if len(buckets[i]) > 0 {
for _, val := range buckets[i] {

chatgpt:
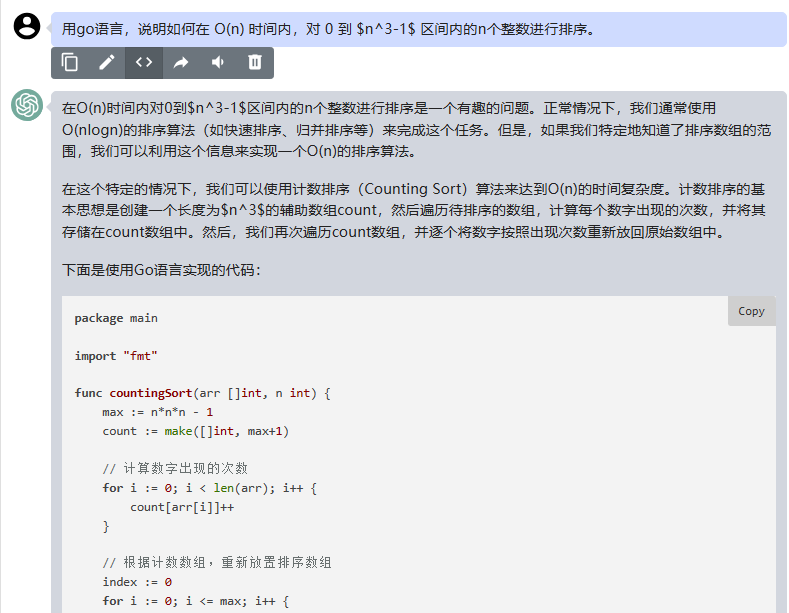
在O(n)时间内对0到 n 3 − 1 n^3-1 n3−1区间内的n个整数进行排序是一个有趣的问题。正常情况下,我们通常使用O(nlogn)的排序算法(如快速排序、归并排序等)来完成这个任务。但是,如果我们特定地知道了排序数组的范围,我们可以利用这个信息来实现一个O(n)的排序算法。
在这个特定的情况下,我们可以使用计数排序(Counting Sort)算法来达到O(n)的时间复杂度。计数排序的基本思想是创建一个长度为 n 3 n^3 n3的辅助数组count,然后遍历待排序的数组,计算每个数字出现的次数,并将其存储在count数组中。然后,我们再次遍历count数组,并逐个将数字按照出现次数重新放回原始数组中。
下面是使用Go语言实现的代码:
package main
import "fmt"
func countingSort(arr []int, n int) {
max := n*n*n - 1
count := make([]int, max+1)
// 计算数字出现的次数
for i := 0; i < len(arr); i++ {
count[arr[i]]++
}
// 根据计数数组,重新放置排序数组
index := 0
for i := 0; i <= max; i++ {
for count[i] > 0 {
arr[index] = i
index++
count[i]--
}
}
}
func main() {
n := 10 // 数组大小
arr := []int{100, 222, 5, 77, 444, 333, 111, 999, 888, 666}
countingSort(arr, n)
fmt.Println("排序后的数组:", arr)
}
这段代码首先创建了一个辅助数组count,大小为 n 3 n^3 n3,然后遍历待排序的数组,计算每个数字出现的次数,并将其存储在count数组中。接下来,我们再次遍历count数组,并按照数字出现的次数,逐个将数字重新放回原始数组中。最后,打印排序后的数组。
这个算法的时间复杂度是O(n),因为我们需要遍历待排序的数组两次。但需要注意的是,计数排序的空间复杂度为O(n^3),所以如果n很大,可能会占用过多的内存。