在前文中,讲到了因为实际项目的需要,调研了一下当前比较好用字符串查询匹配算法,感兴趣的话可以直接看下:
《pyahocorasick——基于AC自动机的python高效字符串匹配实践》
本文的主要目的同前文相同,这里主要是介绍一下另一个好用的字符串查询匹配模块——marisa-trie,官方项目地址在这里,如下所示:
可以看到:目前也是将近1k的star量,略高于前文的AC自动机算法。
marisa-trie模块是一个Python库,提供了用于高效存储和检索字符串键的数据结构。它基于Trie(字典树)数据结构,并使用了高度压缩的表示形式,以提供快速的查找和低内存消耗。
marisa-trie模块的详细特性介绍如下所示:
-
高效的字符串检索:marisa-trie使用了Trie数据结构,可以有效地进行字符串的存储和检索。它支持高效的前缀搜索、模糊搜索和范围搜索等操作。
-
压缩存储:该模块使用了高度压缩的表示形式,可以大幅减小存储空间的需求。这在需要存储大量字符串键的场景下特别有用,可以节省内存和磁盘空间。
-
快速查找:由于采用了Trie数据结构,marisa-trie可以在接近常数时间复杂度下进行查找操作。这使得它非常适合需要高性能的字符串键查找任务。
-
支持可排序键:marisa-trie允许您存储和检索可排序的键。这使得它在需要对字符串键进行排序和范围查询的应用中非常有用。
-
简单易用:该模块提供了简单而直观的API,易于使用和集成到您的Python项目中。
marisa-trie算法是基于Trie(字典树)数据结构开发构建的,并使用了高度压缩的表示形式。下面是marisa-trie的算法构建原理的详细解释:
-
Trie数据结构:Trie是一种树形数据结构,用于存储和检索字符串集合。它由根节点开始,每个节点代表一个字符,每条路径表示一个字符串。通过在树中的路径上移动,可以完成对字符串的查找操作。
-
构建Trie:为了构建marisa-trie,首先需要将字符串键插入Trie中。对于每个字符串键,从根节点开始,按照字符顺序依次向下遍历Trie,并在需要时创建新的节点。当遇到字符串的结束字符或无法继续匹配时,将该节点标记为终止节点。
-
排序节点:在构建完Trie后,需要对节点进行排序。排序的目的是为了后续的压缩步骤做准备。marisa-trie使用了特定的排序算法来保持Trie中字符串键的顺序。
-
压缩表示:一旦节点排序完成,marisa-trie使用了一种高度压缩的表示形式。它将具有相同前缀的节点合并为一个共享前缀节点。这样可以大大减小存储空间的需求,尤其是对于具有大量共享前缀的字符串键。
-
完成构建:一旦压缩表示完成,marisa-trie的构建就完成了。这样构建的marisa-trie数据结构可以在接近常数时间复杂度下进行高效的字符串键查找。
marisa-trie的算法构建原理使得它成为一种有效的数据结构,适用于需要高性能和低内存消耗的字符串键存储和检索任务。
简单的介绍就到这里,接下来我们来实地实践分析一下模块的应用性能。同上文使用相同的数据,核心代码实现如下所示:
patterns = ['an', 'un', 'is']
trie = marisa_trie.Trie(patterns)
text = 'In quiet solitude, peace is found,Where thoughts can wander, unbound.'
results = []
for i in range(len(text)):
matches = trie.prefixes(text[i:])
for matche in matches:
results.append((matche,i,i+len(matche)))
print(results)结果输出如下所示:
[('is', 25, 27), ('un', 30, 32), ('an', 50, 52), ('an', 54, 56), ('un', 61, 63), ('un', 65, 67)]这里面每个子对象目标都是一个三元组数据,第一个元素就是查找出来的目标对象字符串,后面两个数字表示的就是当前匹配到的字符串在原始字符串文本中的开始索引和结束索引。
接下来我们想要实地测试一下该模块的查询匹配效率,编写测试代码生成随机字符串如下所示:
base_list=['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U',
'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p',
'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z']
print(len(base_list))
all_list=[1,10,100,1000,10000,100000]
t_list=[]
for one_all in all_list:
string=""
for i in range(one_all):
string+="".join(random.sample(base_list,10))
print("string_length: ", len(string))随机构建查询目标,查询1000次,如下所示:
for i in range(1000):
one_str="".join(random.sample(base_list, one_num))
one_patterns.append(one_str)构建marisa_trie匹配查询,如下所示:
trie = marisa_trie.Trie(one_patterns)
results = []
for i in range(len(string)):
matches = trie.prefixes(string[i:])
for matche in matches:
results.append((matche,i,i+len(matche)))接下来我们进行实验,在实验中我们还想探索分析查询子串的长度和时间的关系,这里分别进行实验,如下所示:
【查询子串长度为1】
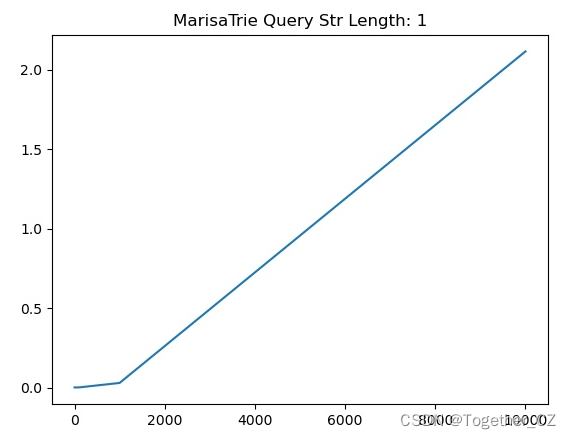
【查询子串长度为2】

【查询子串长度为3】

【查询子串长度为4】

【查询子串长度为5】

【查询子串长度为6】

【查询子串长度为7】

【查询子串长度为8】
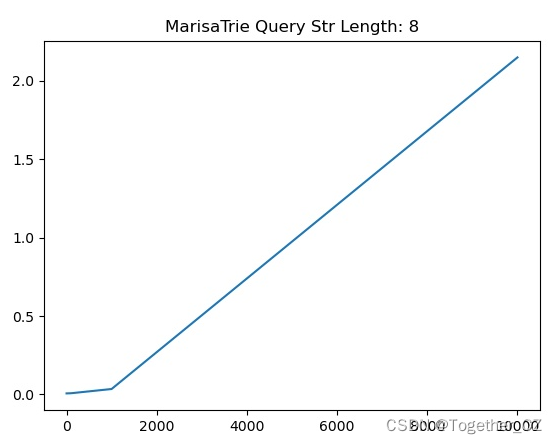
【查询子串长度为9】
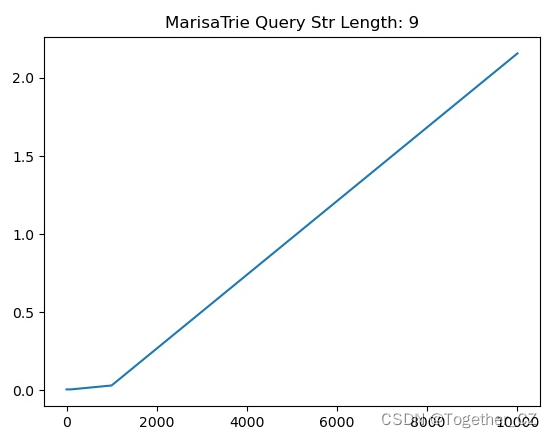
【查询子串长度为10】

从实验测试结果来看:marisa_trie的查询性能跟目标查询子串的长度之间没有明显的关系,我们测试了从1-10连续10组不同长度的子串在相同查询条件下的查询性能发现整体的走势是相同的。
为了直观对比分析,这里我将其绘制整体对比可视化曲线,如下所示:

感兴趣的话都可以试试看,相信会发现他的强大。