---

前言

本章节采用工程设计的方法，推导出电流环PI调节器参数的计算公式，由此来设计永磁同步电机磁场定向控制的电流内环PI调节器参数，并通过Matlab/Simulink对设计的PI调节器进行Bode图分析，最后通过一个设计实例进行仿真验证。
有关永磁同步电机磁场定向控制请阅读：
永磁同步电机（PMSM）磁场定向控制（FOC）及Matlab/Simulink仿真分析

---

一、调节器的工程设计方法

要实现调节器的工程设计方法，首先要简化问题，突出设计的主要矛盾。简化的基本思路就是把调节器的设计过程分成两步：
1、选择调节器的结构，以确保系统稳定，同时满足所需要的稳态精度
2、再选择调节器的参数，以满足系统动态性能指标的要求

选择调节器的结构，使系统能满足所需要的稳态精度，这是设计过程中的第一步。由于III型及III型以上的系统很难稳定，因此常把I型系统和II型系统作为系统设计的目标。

二、电流环PI调节器的参数整定

工程设计方法的原则是：先设计内环后设计外环，因此对于永磁同步电机磁场定向控制系统先设计电流内环PI调节器，将电流环校正为典型I型系统。

2.1.电流环的结构框图

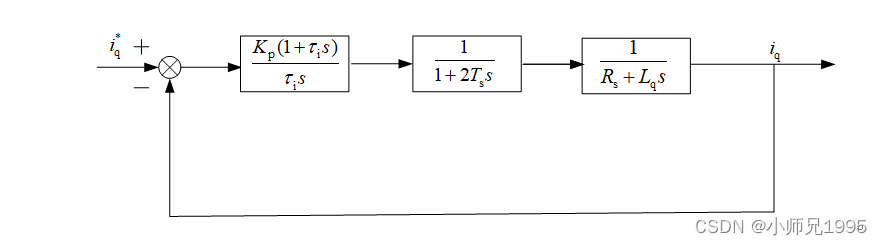
对表贴式SPM永磁同步电机，多采用Id=0来进行控制，使定子电流全部用来产生电磁转矩。由于dq轴电流内环具有对称性和相似的系统特性，所以d轴和q轴的电流调节器参数整定过程类似，本章节以q轴电流调节器参数整定为例进行设计。

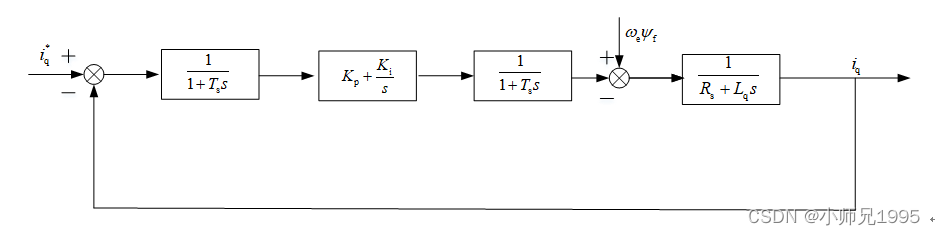
上图为控制系统电流环结构框图，q轴电流给定值iq*与q轴电流反馈值iq的误差为电流环的输入，该误差经过PI调节器输出q轴电压控制信号Uq，通过Uq控制电磁转矩。

通过下述处理，进一步简化电流环的结构框图

电流环的结构框图简化为：

2.2.典型I型系统

取T=0.001，K=100，绘制典型I型系统的Bode图：

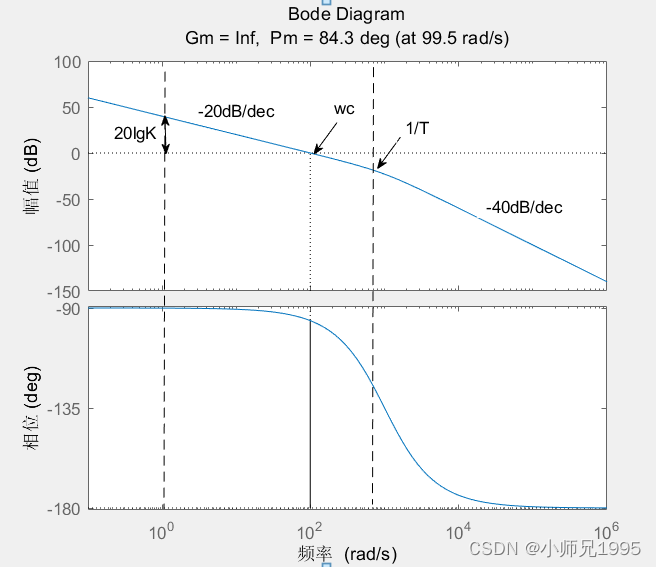
由上图，典型I型系统对数幅频特性的中频段以-20dB/dec斜率穿越0分贝线，只要参数选择能够保证足够的中频带宽度，系统就一定是稳定的。典型I型系统中只包含开环增益K和时间常数T两个参数，时间常数T往往是控制对象本身固有的，系统唯一可变的只有开环增益K，设计时根据性能指标选择K的大小。

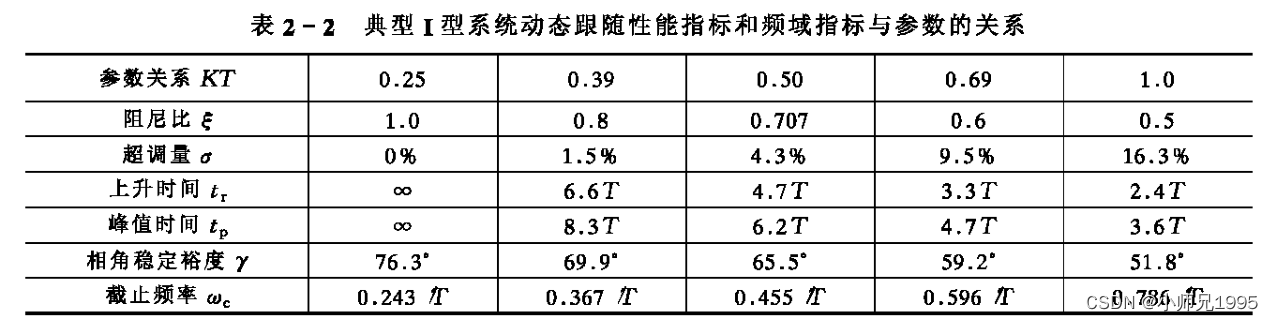
但是上式也表明，K值越大，截止频率wc也就越大，系统的响应越快，但相角裕度越来越小，系统稳定性越来越差，系统快速性和稳定性之间存在矛盾，具体选择参数K时二者应折中处理。工程设计时，一般参照典型I型系统动态性能指标参数表进行K值的选取。

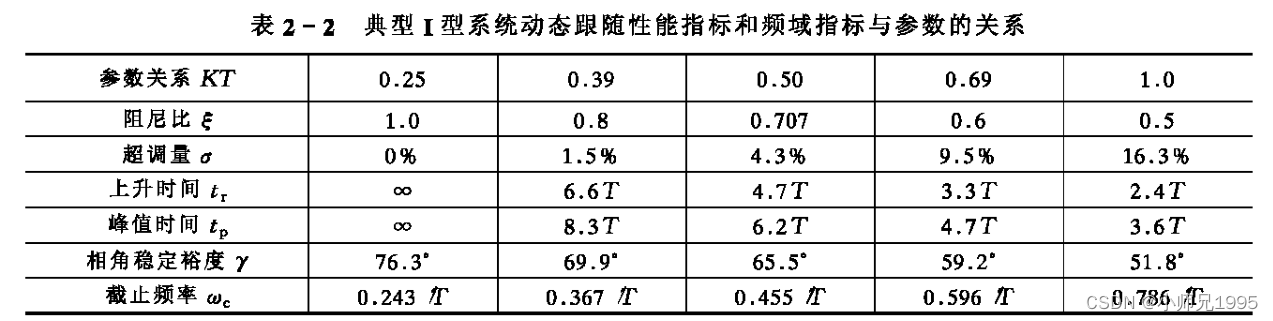
2.3.电流环PI参数整定计算公式

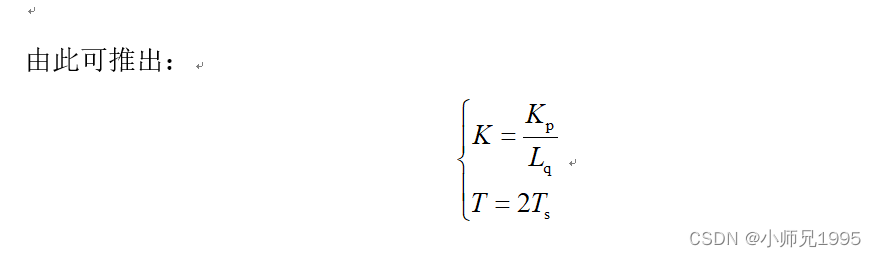
三、电流环PI调节器设计实例

3.1.永磁同步电机磁场定向的电流闭环控制

有关永磁同步电机磁场定向的电流闭环控制的详细分析，请阅读：
永磁同步电机（PMSM）磁场定向控制（FOC）及Matlab/Simulink仿真分析

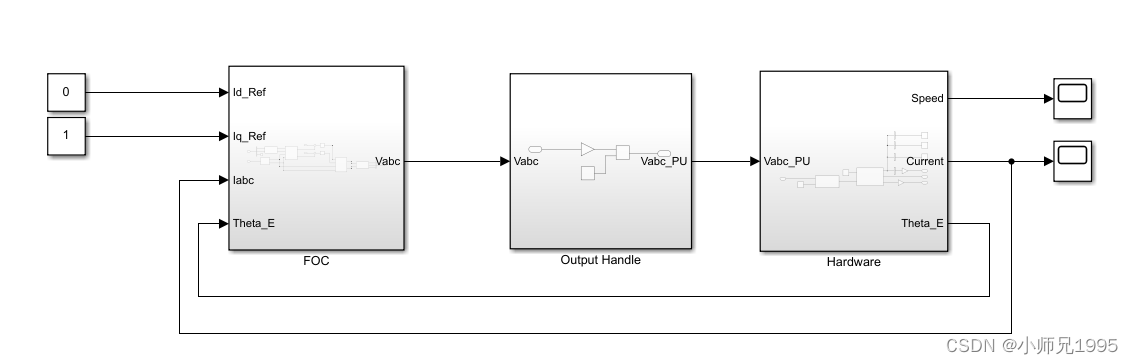
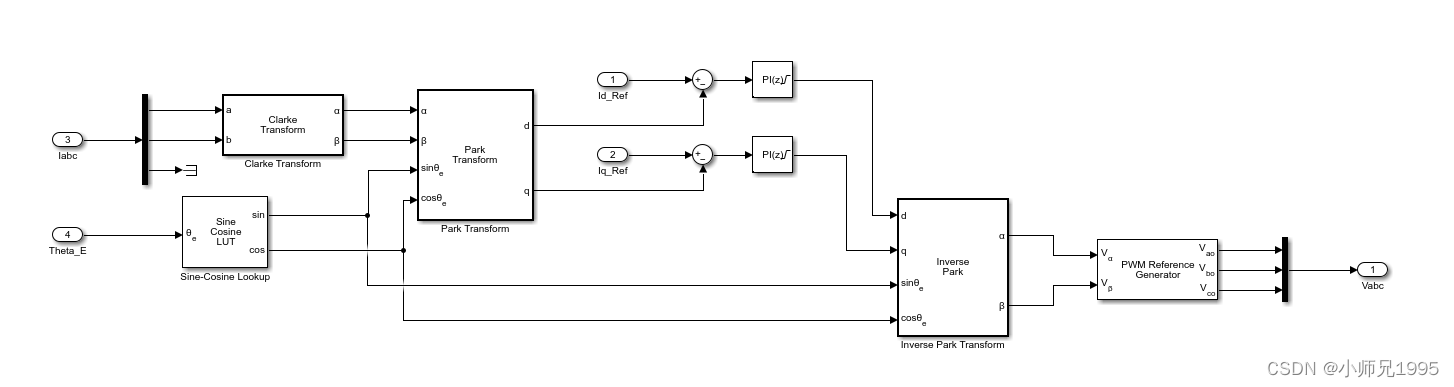
3.2.电流环PI参数计算

电机参数如下：

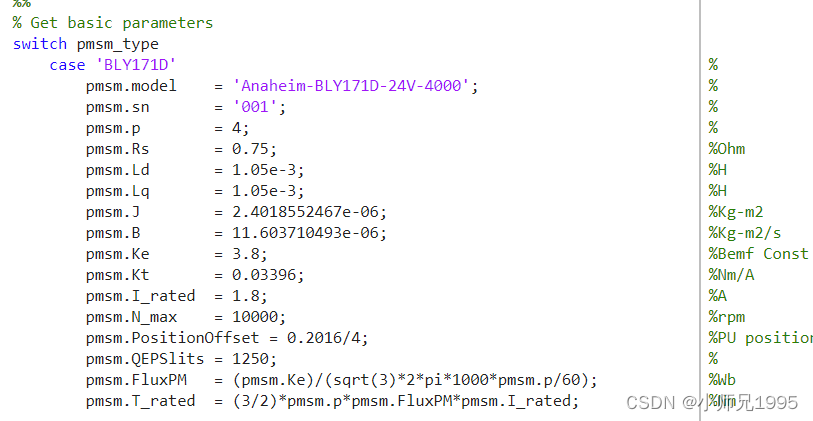
设定电流环采样频率为20KHz，即Ts=0.00005s，由电流环PI调节器参数计算公式得：

绘制该系统的Bode图如下：

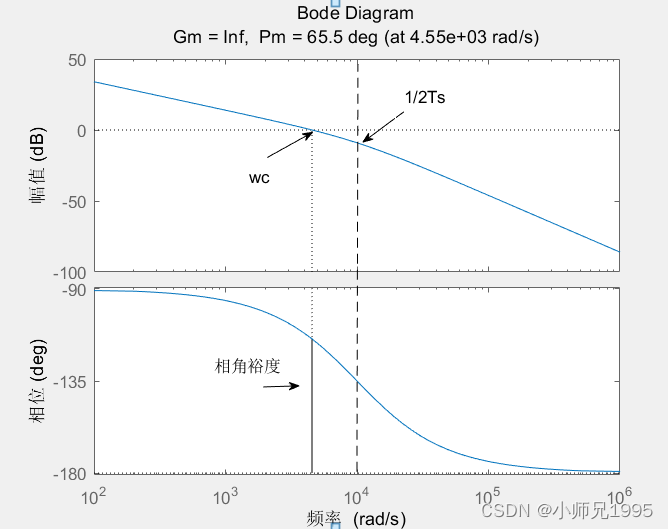
截止频率wc=4550，相角裕度65.5度，与下表KT=0.5所述的系统性能指标一致，表明PI控制器设计成功。

下图为该系统闭环传函的Bode图，从图中可已看出该系统的带宽频率约为7100rad/s

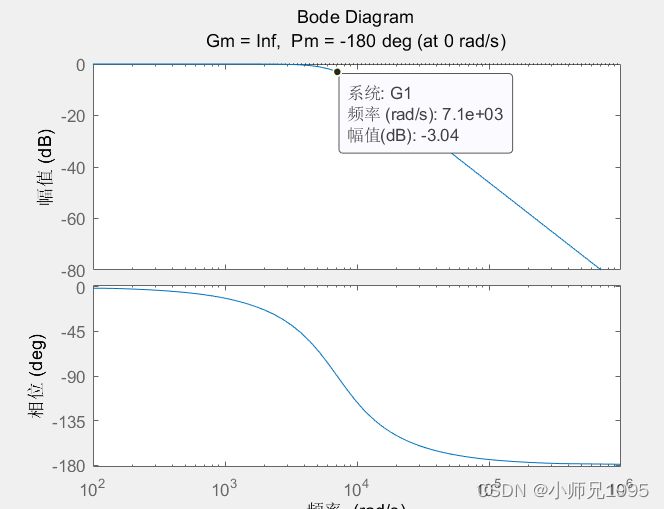
3.3.仿真分析

将Kp=5.25，Ki=3750带入电流闭环仿真模型dq轴的PI调节器中进行仿真分析，结果如下
电机转速：

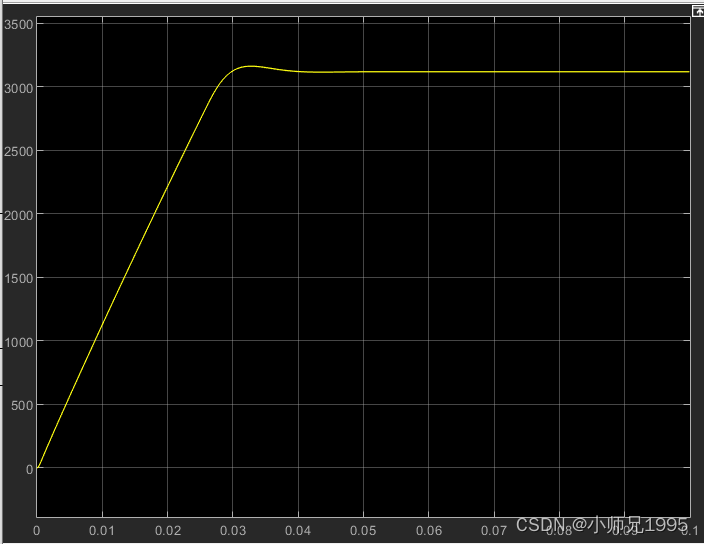
电机定子电流：

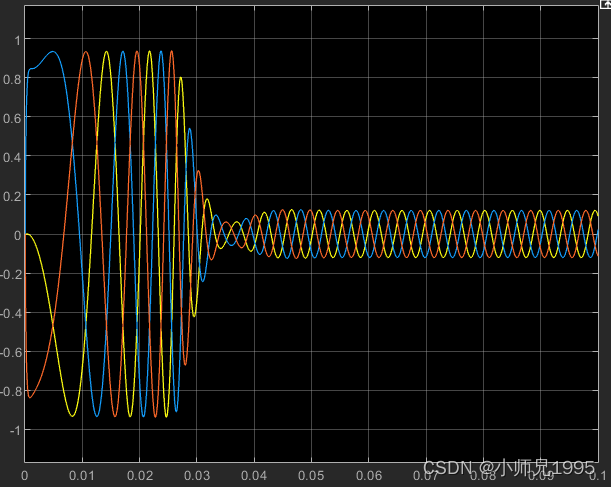
同步旋转坐标系下的定子电流Id、Iq：电机启动时以设定的最大电流1A进行启动，当转速达到稳态值时电流立即降了下来，实现了理想最优的启动过渡过程，反映出电流控制器参数设计成功。

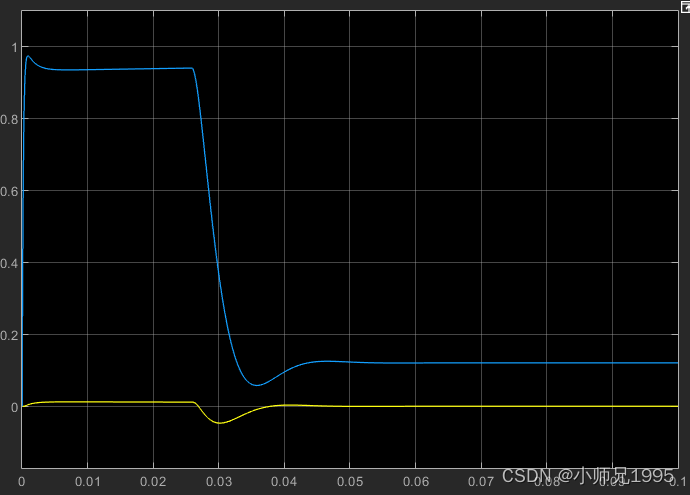
同步旋转坐标系下的定子电压：

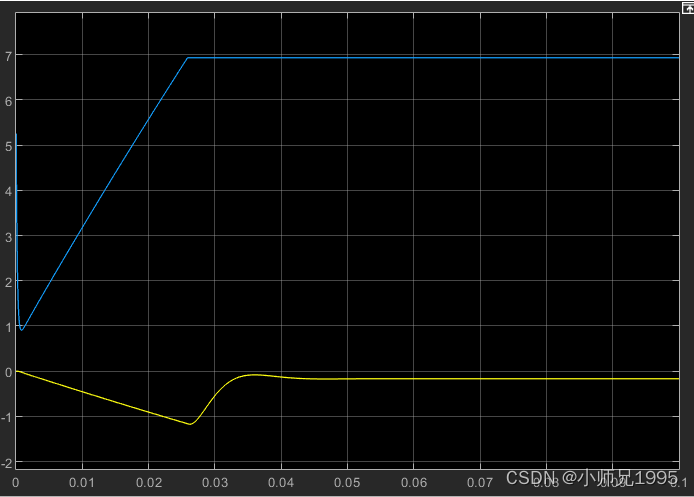
电磁转矩：

---

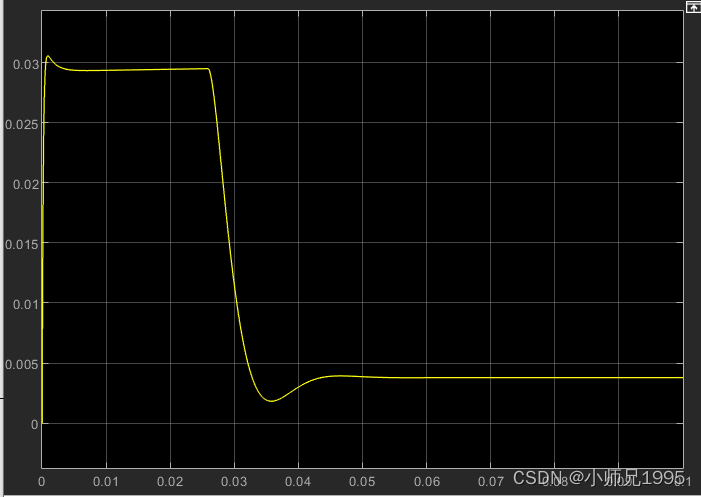
总结

本章节采用工程设计的方法，推导出了电流环PI调节器参数的计算公式，由此来设计永磁同步电机磁场定向控制的电流内环PI调节器参数，并通过Matlab/Simulink对设计的PI调节器进行了Bode图分析，最后通过一个设计实例进行了仿真验证，为后文的分析奠定基础。