本文实现内容
- 各向同性介质波动方程伪谱法波场求解。
- 各项异性介质(VTI、HTI)介质伪谱法波场求解。
- 实现了衰减边界条件、拓展周期边界法。
- 一种波场模拟的数据存储格式
.sfd,提供二进制或文本输入输出。 - 对波场模拟得到的存储数据进行
.gif绘制、.png绘制、地震剖面绘制、单点地震记录绘制等。
伸手党链接
对原理已经很清楚或不需要学习原理的小伙伴可以直接在Github项目链接(https://github.com/Sumbrella/Seismic-Wave-Simulation)下载源代码按README运行。
部分实现结果
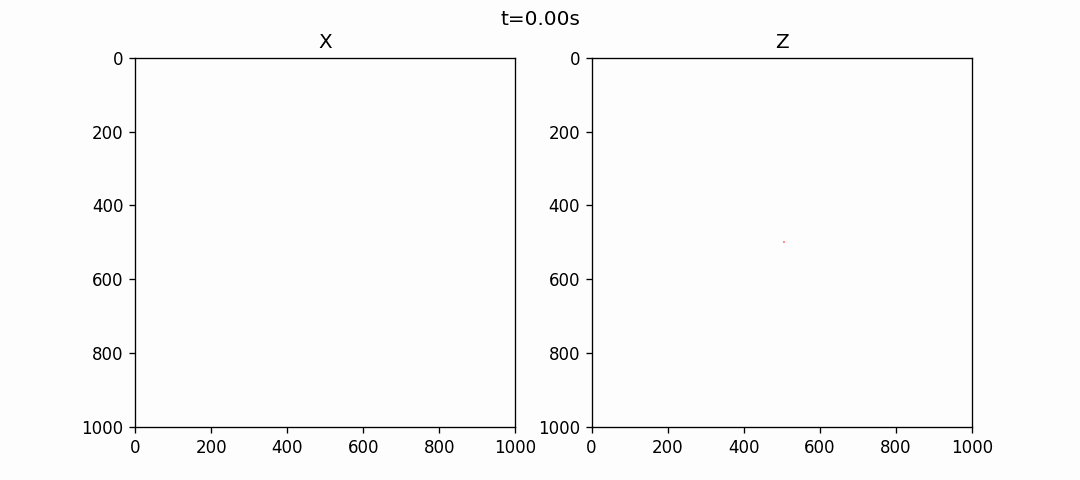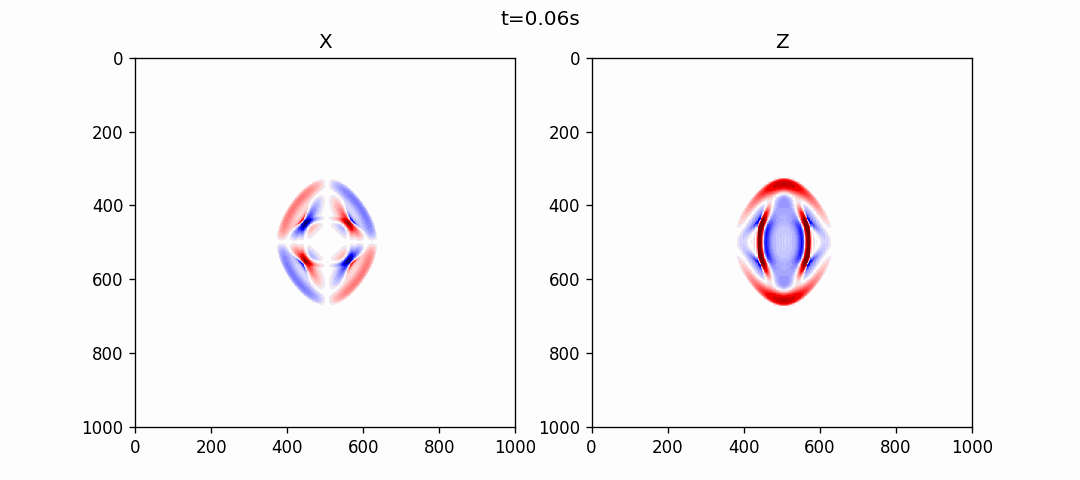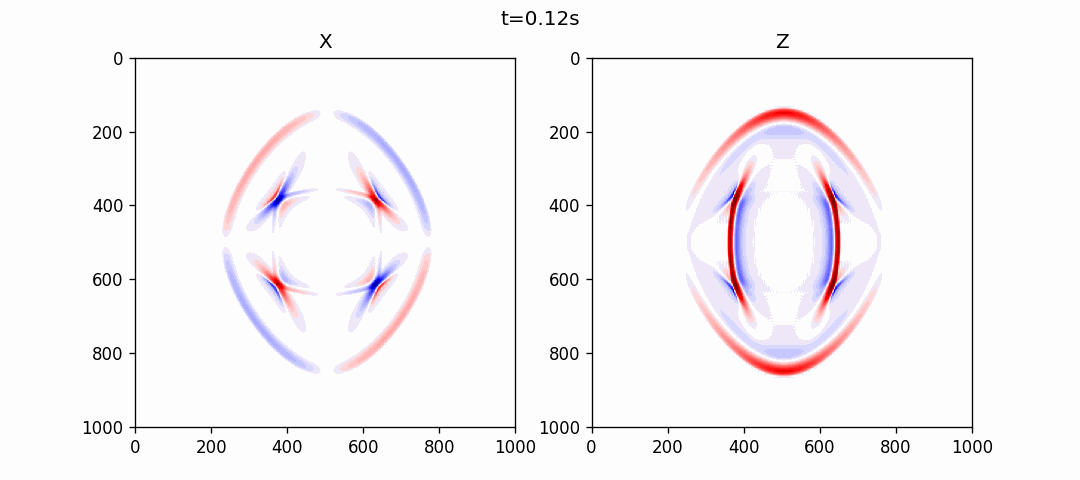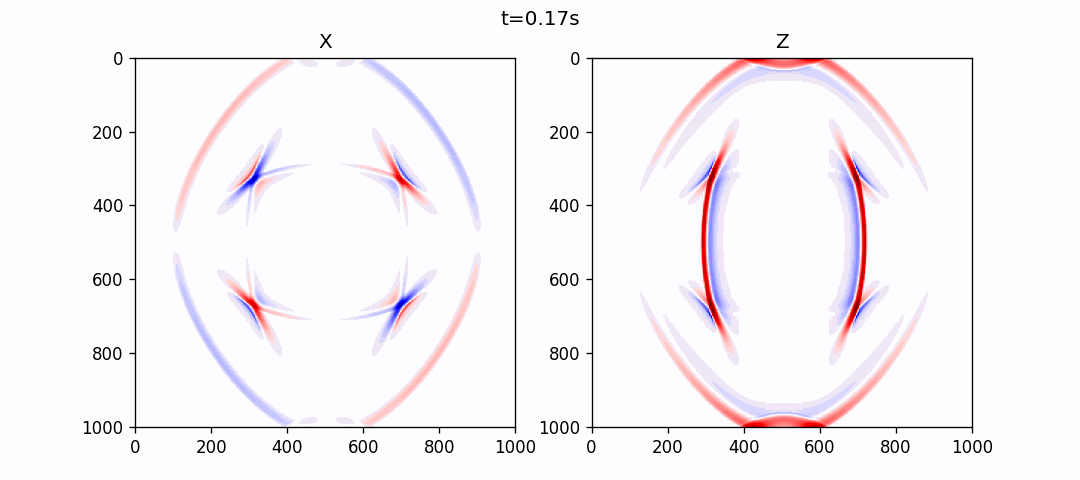
均匀各向同性介质模拟
直立断裂模型
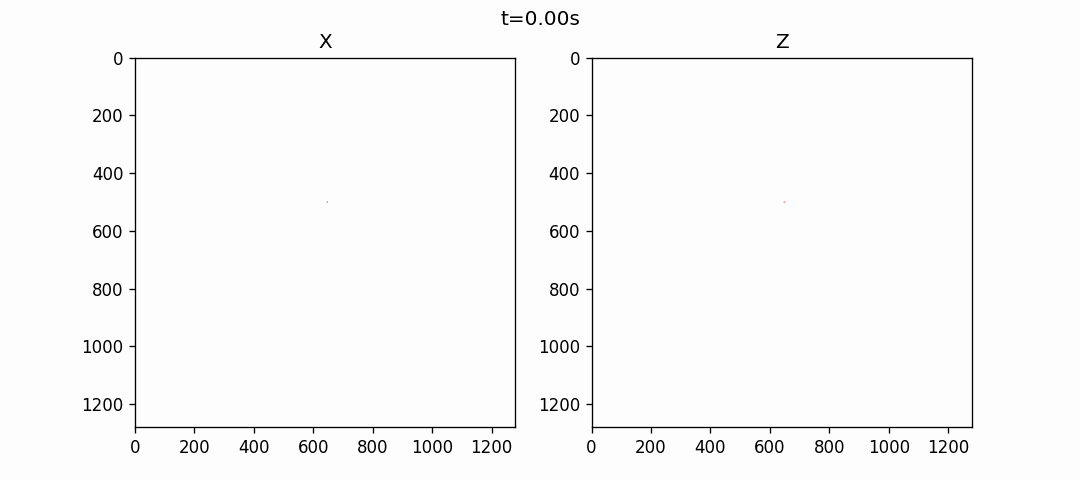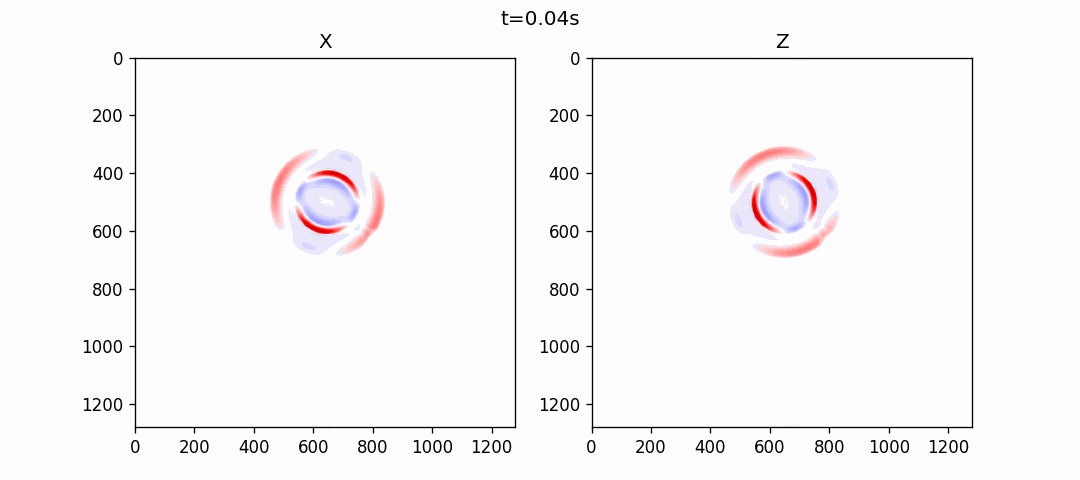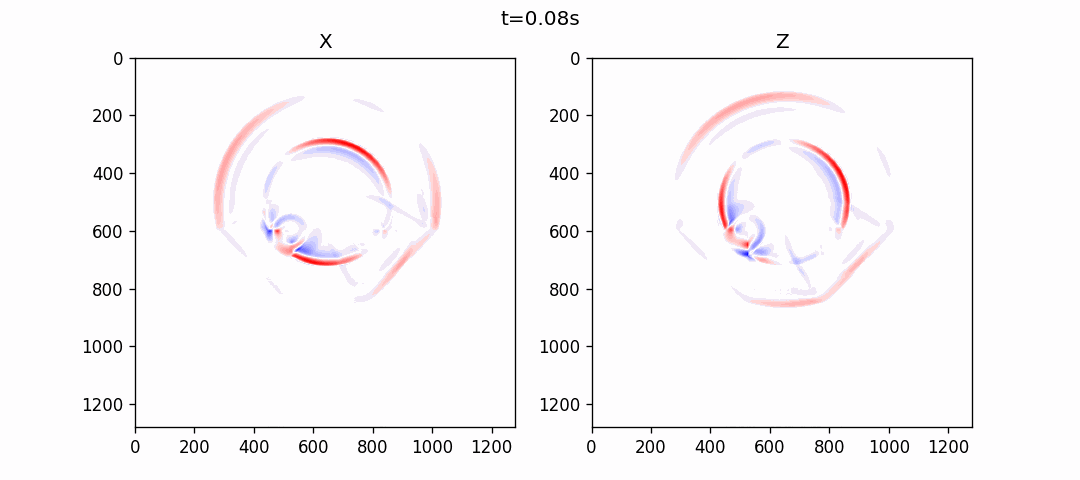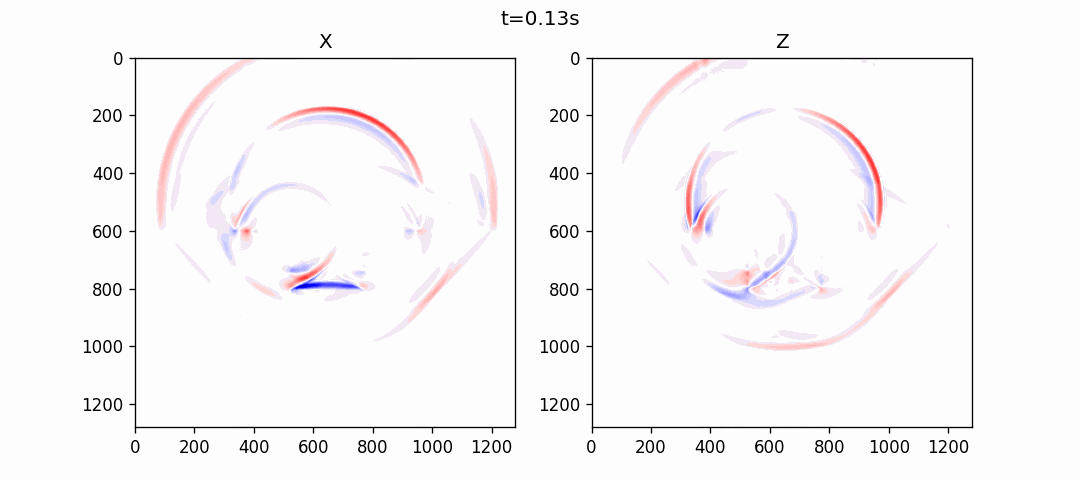
均匀VTI介质模拟
各向同性&HTI横向层状介质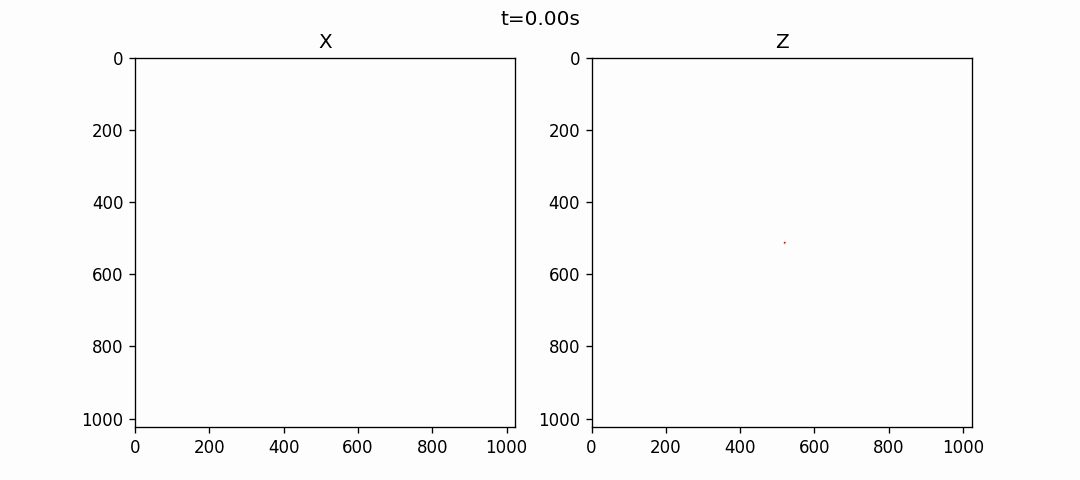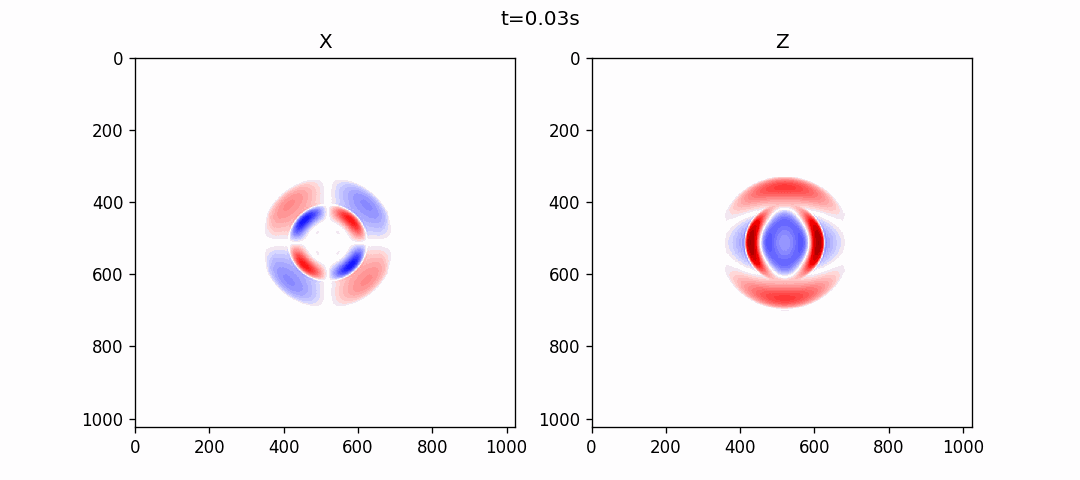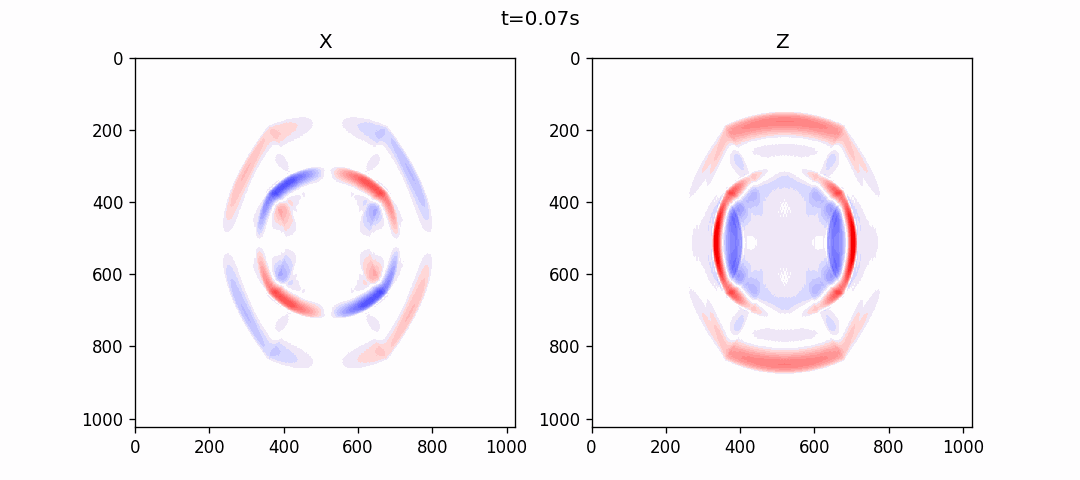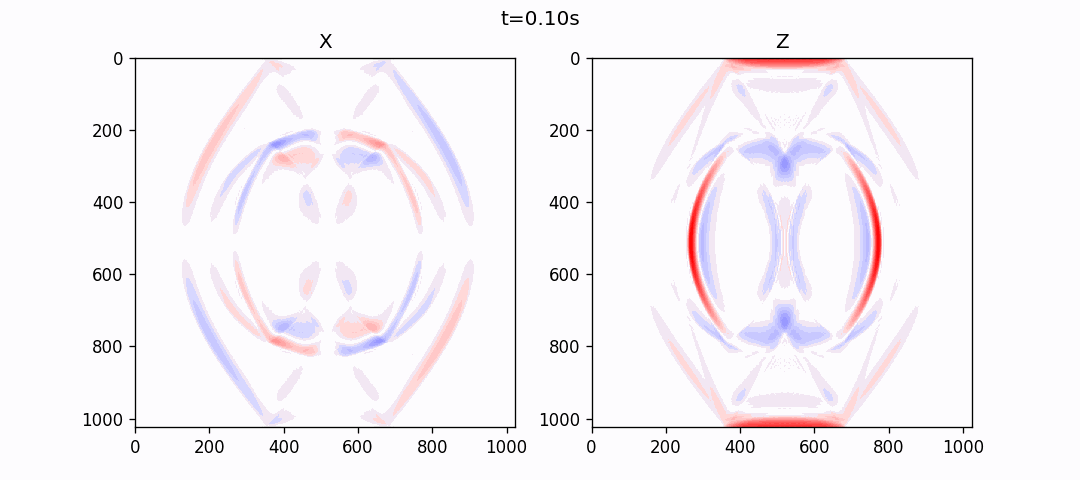
原理
波动方程的建立
弹性介质本构方程
通过广义胡克定律的推理过程,我们可以了解到在介质中的任意一点都存在着六个应力分量,而且每个应力分量与六个应变分量之间有着线性组合的关联,这种关系叫做广义胡克定律, 可表示为:
σ
i
j
=
C
i
j
k
l
ε
k
l
=
∑
k
=
1
3
∑
l
=
1
3
C
i
j
k
l
ε
k
l
.
\sigma_{ij}=C_{ijkl}\varepsilon_{kl}=\sum_{k=1}^{3}\sum_{l=1}^{3}C_{ijkl}\varepsilon_{kl.}
σij=Cijklεkl=k=1∑3l=1∑3Cijklεkl.
其中
C
i
j
k
l
C_{ijkl}
Cijkl为介质的弹性参数,称为刚度张量;依据对称性原则,弹性介质的本构方程经过变化后可以表示成:
[
σ
x
x
σ
y
y
σ
z
z
σ
y
z
σ
z
x
σ
x
y
]
=
[
C
11
C
12
C
13
C
14
C
15
C
16
C
21
C
22
C
23
C
24
C
25
C
26
C
31
C
32
C
33
C
34
C
35
C
36
C
41
C
42
C
43
C
44
C
45
C
46
C
51
C
52
C
53
C
54
C
55
C
56
C
61
C
62
C
63
C
64
C
65
C
66
]
[
ε
x
x
ε
y
y
ε
z
z
ε
y
z
ε
z
x
ε
x
y
]
\left[ \begin{matrix} \sigma_{xx}\\ \sigma_{yy}\\ \sigma_{zz}\\ \sigma_{yz}\\ \sigma_{zx}\\ \sigma_{xy}\\ \end{matrix} \right] = \left[ \begin{matrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & C_{16}\\ C_{21} & C_{22} & C_{23} & C_{24} & C_{25} & C_{26}\\ C_{31} & C_{32} & C_{33} & C_{34} & C_{35} & C_{36}\\ C_{41} & C_{42} & C_{43} & C_{44} & C_{45} & C_{46}\\ C_{51} & C_{52} & C_{53} & C_{54} & C_{55} & C_{56}\\ C_{61} & C_{62} & C_{63} & C_{64} & C_{65} & C_{66} \end{matrix} \right] \left[ \begin{matrix} \varepsilon_{xx}\\ \varepsilon_{yy}\\ \varepsilon_{zz}\\ \varepsilon_{yz}\\ \varepsilon_{zx}\\ \varepsilon_{xy}\\ \end{matrix} \right]
σxxσyyσzzσyzσzxσxy
=
C11C21C31C41C51C61C12C22C32C42C52C62C13C23C33C43C53C63C14C24C34C44C54C64C15C25C35C45C55C65C16C26C36C46C56C66
εxxεyyεzzεyzεzxεxy
可以简写成
σ
=
C
⋅
ε
\sigma=\ C\ \cdot\varepsilon
σ= C ⋅ε
几何方程
介质在受到外界力量的作用,介质会发生弹性形变,使得质点的位移发生改变,由此实现能量的转移和传递。在假设质点的位移函数
u
⃗
=
(
u
x
,
u
y
,
u
z
)
\vec{u}=\left(u_x,u_y,u_z\right)
u=(ux,uy,uz), 在弹性形变不大的情况下,位移与应变满足以下关系式
{
ε
x
x
=
∂
u
x
∂
x
ε
x
y
=
ε
y
x
=
1
2
(
∂
u
x
∂
y
+
∂
u
y
∂
x
)
ε
y
y
=
∂
u
y
∂
y
ε
y
z
=
ε
z
y
=
1
2
(
∂
u
y
∂
z
+
∂
u
z
∂
y
)
ε
z
z
=
∂
u
z
∂
z
ε
z
x
=
ε
x
z
=
1
2
(
∂
u
z
∂
x
+
∂
u
x
∂
z
)
\left\{ \begin{matrix} \varepsilon_{xx} = \dfrac{\partial u_x}{\partial x} & \varepsilon_{xy} = \varepsilon_{yx} = \dfrac{1}{2}(\dfrac{\partial u_x}{\partial y} + \dfrac{\partial u_y}{\partial x})\\ \varepsilon_{yy} = \dfrac{\partial u_y}{\partial y} & \varepsilon_{yz} = \varepsilon_{zy} = \dfrac{1}{2}(\dfrac{\partial u_y}{\partial z} + \dfrac{\partial u_z}{\partial y})\\ \varepsilon_{zz} = \dfrac{\partial u_z}{\partial z} & \varepsilon_{zx} = \varepsilon_{xz} = \dfrac{1}{2}(\dfrac{\partial u_z}{\partial x} + \dfrac{\partial u_x}{\partial z})\\ \end{matrix} \right.
⎩
⎨
⎧εxx=∂x∂uxεyy=∂y∂uyεzz=∂z∂uzεxy=εyx=21(∂y∂ux+∂x∂uy)εyz=εzy=21(∂z∂uy+∂y∂uz)εzx=εxz=21(∂x∂uz+∂z∂ux)
如果令
M
=
[
∂
∂
x
0
0
0
∂
∂
z
∂
∂
y
0
∂
∂
y
0
∂
∂
z
0
∂
∂
x
0
0
∂
∂
z
∂
∂
y
∂
∂
x
0
]
M = \left[ \begin{matrix} \dfrac{\partial}{\partial x} & 0 & 0 & 0 & \dfrac{\partial}{\partial z} & \dfrac{\partial}{\partial y}\\ 0 & \dfrac{\partial}{\partial y} & 0 & \dfrac{\partial}{\partial z} & 0 & \dfrac{\partial}{\partial x}\\ 0 & 0 & \dfrac{\partial}{\partial z} & \dfrac{\partial}{\partial y} &\dfrac{\partial}{\partial x} & 0\\ \end{matrix} \right]
M=
∂x∂000∂y∂000∂z∂0∂z∂∂y∂∂z∂0∂x∂∂y∂∂x∂0
则经过简化后的几何方程形式表示为:
ε
=
M
T
U
\varepsilon=M^TU
ε=MTU
质点位移与应力之间的关系
为了准确描述介质内部质点的位移与应力之间的关系,我们需要建立适当的运动微分方程式。介质内部受到的力可以分为体力和面力两种形式。体力是指在介质内部按体积分布作用的力,而面力则是作用于截面上与其面积成正比的力。在考虑微小形变的情况下,当弹性体受到外力作用并发生微弱形变时,可以近似地满足运动微分方程式。这些方程式描述了质点的位移如何响应于外力以及介质的力学特性:
{
ρ
∂
2
u
x
∂
t
2
=
∂
σ
x
x
∂
x
+
∂
σ
x
y
∂
y
+
∂
σ
x
z
∂
z
+
ρ
f
x
ρ
∂
2
u
y
∂
t
2
=
∂
σ
y
x
∂
x
+
∂
σ
y
y
∂
y
+
∂
σ
y
z
∂
z
+
ρ
f
y
ρ
∂
2
u
z
∂
t
2
=
∂
σ
z
x
∂
x
+
∂
σ
z
y
∂
y
+
∂
σ
z
z
∂
z
+
ρ
f
z
\left\{ \begin{matrix} \rho \dfrac{\partial^2 u_x}{\partial t^2} = \dfrac{\partial \sigma_{xx}}{\partial x} + \dfrac{\partial \sigma_{xy}}{\partial y} + \dfrac{\partial \sigma_{xz}}{\partial z} + \rho f_x\\ \rho \dfrac{\partial^2 u_y}{\partial t^2} = \dfrac{\partial \sigma_{yx}}{\partial x} + \dfrac{\partial \sigma_{yy}}{\partial y} + \dfrac{\partial \sigma_{yz}}{\partial z} + \rho f_y\\ \rho \dfrac{\partial^2 u_z}{\partial t^2} = \dfrac{\partial \sigma_{zx}}{\partial x} + \dfrac{\partial \sigma_{zy}}{\partial y} + \dfrac{\partial \sigma_{zz}}{\partial z} + \rho f_z \end{matrix} \right.
⎩
⎨
⎧ρ∂t2∂2ux=∂x∂σxx+∂y∂σxy+∂z∂σxz+ρfxρ∂t2∂2uy=∂x∂σyx+∂y∂σyy+∂z∂σyz+ρfyρ∂t2∂2uz=∂x∂σzx+∂y∂σzy+∂z∂σzz+ρfz
运动微分方程
结合上面推导出的运动微分方程,几何方程,弹性系数矩阵,我们将三式组合得到三维介质中的运动微分方程:
{
ρ
∂
2
u
x
∂
t
2
=
C
11
∂
2
u
x
∂
x
2
+
(
C
12
+
C
66
)
∂
2
u
y
∂
x
∂
y
+
(
C
13
+
C
55
)
∂
2
u
z
∂
x
∂
z
+
C
66
∂
2
u
x
∂
y
2
+
C
55
∂
2
u
x
∂
z
2
+
ρ
f
x
ρ
∂
2
u
y
∂
t
2
=
C
22
∂
2
u
y
∂
y
2
+
(
C
21
+
C
66
)
∂
2
u
x
∂
x
∂
y
+
(
C
23
+
C
44
)
∂
2
u
z
∂
y
∂
z
+
C
66
∂
2
u
y
∂
x
2
+
C
55
∂
2
u
y
∂
z
2
+
ρ
f
y
ρ
∂
2
u
z
∂
t
2
=
C
33
∂
2
u
z
∂
x
2
+
(
C
31
+
C
55
)
∂
2
u
z
∂
x
∂
z
+
(
C
32
+
C
44
)
∂
2
u
y
∂
y
∂
z
+
C
55
∂
2
u
z
∂
x
2
+
C
44
∂
2
u
z
∂
y
2
+
ρ
f
z
\left\{ \begin{matrix} \rho \dfrac{\partial^2 u_x}{\partial t^2} = C_{11} \dfrac{\partial^2 u_x}{\partial x^2} + (C_{12} + C_{66}) \dfrac{\partial^2 u_y}{\partial x \partial y} + (C_{13} + C_{55}) \dfrac{\partial^2 u_z}{\partial x \partial z} + C_{66} \dfrac{\partial^2 u_x}{\partial y^2} + C_{55} \dfrac{\partial^2 u_x}{\partial z^2} + \rho f_x\\ \rho \dfrac{\partial^2 u_y}{\partial t^2} = C_{22} \dfrac{\partial^2 u_y}{\partial y^2} + (C_{21} + C_{66}) \dfrac{\partial^2 u_x}{\partial x \partial y} + (C_{23} + C_{44}) \dfrac{\partial^2 u_z}{\partial y \partial z} + C_{66} \dfrac{\partial^2 u_y}{\partial x^2} + C_{55} \dfrac{\partial^2 u_y}{\partial z^2} + \rho f_y\\ \rho \dfrac{\partial^2 u_z}{\partial t^2} = C_{33} \dfrac{\partial^2 u_z}{\partial x^2} + (C_{31} + C_{55}) \dfrac{\partial^2 u_z}{\partial x \partial z} + (C_{32} + C_{44}) \dfrac{\partial^2 u_y}{\partial y \partial z} + C_{55} \dfrac{\partial^2 u_z}{\partial x^2} + C_{44} \dfrac{\partial^2 u_z}{\partial y^2} + \rho f_z \end{matrix} \right.
⎩
⎨
⎧ρ∂t2∂2ux=C11∂x2∂2ux+(C12+C66)∂x∂y∂2uy+(C13+C55)∂x∂z∂2uz+C66∂y2∂2ux+C55∂z2∂2ux+ρfxρ∂t2∂2uy=C22∂y2∂2uy+(C21+C66)∂x∂y∂2ux+(C23+C44)∂y∂z∂2uz+C66∂x2∂2uy+C55∂z2∂2uy+ρfyρ∂t2∂2uz=C33∂x2∂2uz+(C31+C55)∂x∂z∂2uz+(C32+C44)∂y∂z∂2uy+C55∂x2∂2uz+C44∂y2∂2uz+ρfz
忽略y分量,只考虑二维空间的
x
,
z
x, z
x,z两个分量,可以得到二维的各项同性弹性介质波动方程:
{
ρ
∂
2
u
x
∂
t
2
=
C
11
∂
2
u
x
∂
x
2
+
(
C
13
+
C
55
)
∂
2
u
z
∂
x
∂
z
+
C
55
∂
2
u
x
∂
z
2
+
ρ
f
x
ρ
∂
2
u
z
∂
t
2
=
C
33
∂
2
u
z
∂
x
2
+
(
C
31
+
C
55
)
∂
2
u
z
∂
x
∂
z
+
C
55
∂
2
u
z
∂
x
2
+
ρ
f
z
\left\{ \begin{matrix} \rho \dfrac{\partial^2 u_x}{\partial t^2} = C_{11} \dfrac{\partial^2 u_x}{\partial x^2} + (C_{13} + C_{55}) \dfrac{\partial^2 u_z}{\partial x \partial z} + C_{55} \dfrac{\partial^2 u_x}{\partial z^2} + \rho f_x\\ \rho \dfrac{\partial^2 u_z}{\partial t^2} = C_{33} \dfrac{\partial^2 u_z}{\partial x^2} + (C_{31} + C_{55}) \dfrac{\partial^2 u_z}{\partial x \partial z} + C_{55} \dfrac{\partial^2 u_z}{\partial x^2} + \rho f_z \end{matrix} \right.
⎩
⎨
⎧ρ∂t2∂2ux=C11∂x2∂2ux+(C13+C55)∂x∂z∂2uz+C55∂z2∂2ux+ρfxρ∂t2∂2uz=C33∂x2∂2uz+(C31+C55)∂x∂z∂2uz+C55∂x2∂2uz+ρfz
对于各向异性介质,他们与各向同性的差异仅仅在弹性系数矩阵上,按同样的方法可以得到VTI介质的弹性波动方程、HTI介质的弹性波动方程:
VTI介质
{
ρ
∂
2
u
∂
t
2
=
C
11
∂
2
u
∂
x
2
+
(
C
13
+
C
66
)
∂
2
w
∂
x
∂
z
+
C
66
∂
2
u
∂
z
2
+
f
x
ρ
∂
2
w
∂
t
2
=
(
C
55
+
C
31
)
∂
2
u
∂
x
2
+
C
55
∂
2
w
∂
x
2
+
C
33
∂
2
w
∂
z
2
+
f
z
\newcommand{\ppat}[2]{\dfrac{\partial^2 #1}{\partial #2^2}} \newcommand{\patt}[3]{\dfrac{\partial^2 #1}{\partial #2 \partial #3}} \left\{ \begin{aligned} \rho \ppat{u}{t} = C_{11} \ppat{u}{x} + (C_{13} + C_{66}) \dfrac{\partial^2 w}{\partial x \partial z} + C_{66} \ppat{u}{z} + f_{x}\\ \rho \ppat{w}{t} = (C_{55} + C_{31}) \ppat{u}{x} + C_{55} \ppat{w}{x} + C_{33} \ppat{w}{z} + f_{z}\\ \end{aligned} \right.
⎩
⎨
⎧ρ∂t2∂2u=C11∂x2∂2u+(C13+C66)∂x∂z∂2w+C66∂z2∂2u+fxρ∂t2∂2w=(C55+C31)∂x2∂2u+C55∂x2∂2w+C33∂z2∂2w+fz
HTI介质
{
ρ
∂
2
u
∂
t
2
=
C
11
∂
2
u
∂
x
2
+
(
C
13
+
C
55
)
∂
2
w
∂
x
∂
z
+
C
55
∂
2
u
∂
z
2
+
f
x
ρ
∂
2
w
∂
t
2
=
C
55
∂
2
w
∂
x
2
+
(
C
13
+
C
55
)
∂
2
u
∂
x
∂
z
+
C
33
∂
2
w
∂
z
2
+
f
z
\newcommand{\ppat}[2]{\dfrac{\partial^2 #1}{\partial #2^2}} \newcommand{\patt}[3]{\dfrac{\partial^2 #1}{\partial #2 \partial #3}} \left\{\begin{aligned} \rho \ppat{u}{t} &= C_{11} \ppat{u}{x} + (C_{13} + C_{55}) \patt{w}{x}{z} + C_{55}\ppat{u}{z} + f_x\\ \rho \ppat{w}{t}& = C_{55} \ppat{w}{x} + (C_{13} + C_{55}) \patt{u}{x}{z} + C_{33} \ppat{w}{z} + f_z \end{aligned}\right.
⎩
⎨
⎧ρ∂t2∂2uρ∂t2∂2w=C11∂x2∂2u+(C13+C55)∂x∂z∂2w+C55∂z2∂2u+fx=C55∂x2∂2w+(C13+C55)∂x∂z∂2u+C33∂z2∂2w+fz
伪谱法求导原理
首先,我们将波函数
u
(
x
)
u(x)
u(x)展开为傅里叶级数形式:
u
(
x
)
=
∑
k
=
−
∞
+
∞
c
k
e
i
k
x
u(x) = \sum_{k=-\infty}^{+\infty}c_k e^{ikx}
u(x)=k=−∞∑+∞ckeikx
这里的
c
k
c_k
ck 是傅里叶系数,代表了波函数在不同频率分量上的振幅。我们可以通过对波函数进行采样来估计这些系数。
然后,我们选择一组离散采样点
x
j
x_j
xj,其中
j
=
0
,
1
,
2
,
…
,
N
−
1
j = 0, 1, 2, \ldots, N-1
j=0,1,2,…,N−1,并计算在这些点上的函数值
u
(
x
j
)
u(x_j)
u(xj)。根据采样定理,如果我们的采样频率足够高,那么我们可以准确地还原原始函数。
接下来,我们引入离散傅里叶变换(Discrete Fourier Transform,DFT)。通过将连续傅里叶级数转化为离散形式,我们可以得到离散傅里叶变换的表达式:
u
N
(
x
j
)
=
∑
k
=
−
∞
+
∞
c
k
e
i
k
x
j
u_N(x_j) = \sum_{k=-\infty}^{+\infty}c_ke^{ikx_j}
uN(xj)=k=−∞∑+∞ckeikxj
这里的
u
N
(
x
j
)
u_N(x_j)
uN(xj) 表示在离散采样点处的逼近函数。
我们可以使用傅立叶变换的微分性质:
f
^
′
(
k
)
=
2
π
i
k
F
(
k
)
\hat f'(k) = 2\pi i k F(k)
f^′(k)=2πikF(k)
来求取函数的导数,在上面的条件下,可以将离散傅立叶微分算子表示为:
d
f
(
x
)
d
x
=
d
f
(
m
Δ
x
)
d
x
=
∑
n
=
0
N
−
1
i
n
Δ
k
F
(
n
Δ
k
)
e
i
2
π
m
n
/
N
,
m
=
1
,
2
,
⋯
,
N
−
1
(1)
\dfrac{\mathrm d f(x)}{\mathrm d x} = \dfrac{\mathrm d f(m\Delta x)}{\mathrm d x} = \sum_{n=0}^{N-1} in \Delta k F(n\Delta k)e^{i2\pi mn/N}, m =1, 2, \cdots, N-1 \tag{1}
dxdf(x)=dxdf(mΔx)=n=0∑N−1inΔkF(nΔk)ei2πmn/N,m=1,2,⋯,N−1(1)
其中,
F
(
n
Δ
k
)
=
1
N
∑
m
=
0
N
−
1
f
(
n
Δ
x
)
e
−
i
2
π
m
n
/
N
F(n\Delta k) = \dfrac{1}{N} \sum_{m=0}^{N-1}f(n\Delta x) e^{-i2\pi mn /N}
F(nΔk)=N1m=0∑N−1f(nΔx)e−i2πmn/N
最后我们可以使用离散傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT)来计算逼近函数
u
N
(
x
j
)
u_N(x_j)
uN(xj)。
程序实现
伪谱法的程序实现
一维数据的伪谱法
我们假设数据为 u ( x ) u(x) u(x), 离散点依次为 1 , 2 , ⋯ 1, 2, \cdots 1,2,⋯, 用 i i i表示下标,对于(1)式,我们需要分成三步来计算。
- 计算 u ( x ) u(x) u(x)的傅立叶变换 F ( f ) F(f) F(f)。
- 对 F ( f ) F(f) F(f)在频率域乘以求导因子 i k ik ik, 得到 F p ( f ) F_p(f) Fp(f)
- 对 F p ( f ) F_p(f) Fp(f)作傅立叶逆变换得到 u ′ ( x ) u'(x) u′(x)。
import numpy as np
def psm(u, k):
"""
u: 一维波场。
k: 离散方向的波数。
"""
f = np.fft.fft(u)
ks = np.array(
[i if i <= n / 2 else i - n for i in range(n)]
) * k
return np.ifft(i * k * f)
二维伪谱法的实现
二维的伪谱法与一纬的伪谱法实现过程一致,只不过要注意,由于需要对两个维度进行傅立叶变换,因此进行傅立叶变换的维度不同。
def cal_dx(u, kx):
return np.real(np.fft.ifft2(1j * kx * np.fft.fft2(u)))
def cal_dz(u, kz):
return np.real(np.fft.ifft2(1j * kz * np.fft.fft2(u.T))).T
对两个不同维度进行伪谱法求导的时候,如果是在列方向上使用伪谱法需要注意求导。
代码中的kx, kz为x方向和z方向的波数。
时间域上的差分方程
为了进行迭代,我们可以将时间域的二阶导数简单的使用差分方程来替代,
首先将模拟时间均分,每两个时间间隔为
Δ
t
\Delta t
Δt, 第
k
k
k步的波长为
u
k
u_k
uk, 则有:
{
∂
u
k
∂
t
≈
u
k
−
u
k
−
1
Δ
t
∂
2
u
k
∂
t
2
≈
u
k
−
2
u
k
−
1
+
u
k
−
2
Δ
t
2
\begin{cases} \dfrac{\partial u_{k}}{\partial t} \approx \dfrac{ u_{k} - u_{k-1} }{\Delta t} \\ \dfrac{\partial^2 u_k}{\partial t^2} \approx \dfrac{u_{k} - 2u_{k-1} + u_{k-2}}{\Delta t^2} \end{cases}
⎩
⎨
⎧∂t∂uk≈Δtuk−uk−1∂t2∂2uk≈Δt2uk−2uk−1+uk−2
离散方程推导
根据上面推导出的各向同性介质在二维情况下的弹性波动方程,即下式:
{
ρ
∂
2
u
x
∂
t
2
=
C
11
∂
2
u
x
∂
x
2
+
(
C
13
+
C
55
)
∂
2
u
z
∂
x
∂
z
+
C
55
∂
2
u
x
∂
z
2
+
ρ
f
x
ρ
∂
2
u
z
∂
t
2
=
C
33
∂
2
u
z
∂
x
2
+
(
C
31
+
C
55
)
∂
2
u
z
∂
x
∂
z
+
C
55
∂
2
u
z
∂
x
2
+
ρ
f
z
\left\{ \begin{matrix} \rho \dfrac{\partial^2 u_x}{\partial t^2} = C_{11} \dfrac{\partial^2 u_x}{\partial x^2} + (C_{13} + C_{55}) \dfrac{\partial^2 u_z}{\partial x \partial z} + C_{55} \dfrac{\partial^2 u_x}{\partial z^2} + \rho f_x\\ \rho \dfrac{\partial^2 u_z}{\partial t^2} = C_{33} \dfrac{\partial^2 u_z}{\partial x^2} + (C_{31} + C_{55}) \dfrac{\partial^2 u_z}{\partial x \partial z} + C_{55} \dfrac{\partial^2 u_z}{\partial x^2} + \rho f_z \end{matrix} \right.
⎩
⎨
⎧ρ∂t2∂2ux=C11∂x2∂2ux+(C13+C55)∂x∂z∂2uz+C55∂z2∂2ux+ρfxρ∂t2∂2uz=C33∂x2∂2uz+(C31+C55)∂x∂z∂2uz+C55∂x2∂2uz+ρfz
在空间域上使用伪谱法,于是有:
ρ
∂
2
u
x
∂
t
2
=
C
11
p
s
m
x
(
p
s
m
x
(
u
x
)
)
+
(
C
13
+
C
55
)
p
s
m
x
(
p
s
m
z
(
u
z
)
)
+
C
55
p
s
m
z
(
p
s
m
z
(
u
x
)
)
+
ρ
f
x
\rho \dfrac{\partial^2 u_x}{\partial t^2} =C_{11} \mathrm{psm}_x (\mathrm{psm_x}(u_x)) + (C_{13} + C_{55})\mathrm{psm}_x(\mathrm{psm}_z(u_z) ) + C_{55} \mathrm{psm}_z(\mathrm{psm_z}(u_x)) + \rho f_x
ρ∂t2∂2ux=C11psmx(psmx(ux))+(C13+C55)psmx(psmz(uz))+C55psmz(psmz(ux))+ρfx
假设上式的右侧为等式
A
\mathbf{A}
A, 在时间域上使用有限差分法,则有:
u k = 2 u k − 1 − u k − 2 + Δ t 2 ρ A + Δ t 2 f (1) u_{k} = 2u_{k-1} -u_{k-2} + \dfrac{ \Delta t^2 } {\rho} \mathbf{A} + \Delta t^2 f \tag{1} uk=2uk−1−uk−2+ρΔt2A+Δt2f(1)
各向均匀介质波场模拟
根据 (1) 式, 我们假设有各向均匀介质参数如下表所示:
| 参数名 | 参数值 | 参数单位 |
|---|---|---|
| xmin | 0 0 0 | m \mathrm{m} m |
| xmax | 1024 1024 1024 | m \mathrm{m} m |
| ymin | 0 0 0 | m \mathrm{m} m |
| ymax | 1024 1024 1024 | m \mathrm{m} m |
| t | 0.2 0.2 0.2 | s \mathrm{s} s |
| dx | 5 5 5 | m \mathrm{m} m |
| dy | 5 5 5 | m \mathrm{m} m |
| dt | 2 e − 4 2e^{-4} 2e−4 | s \mathrm{s} s |
| 子波主频 f m f_m fm | 40 40 40 | H z \mathrm{Hz} Hz |
| C 11 C_{11} C11 | 300 0 2 ∗ 2.7 3000^2 * 2.7 30002∗2.7 | G P a \mathrm{GPa} GPa |
| C 12 C_{12} C12 | 150 0 2 ∗ 2.7 1500^2 * 2.7 15002∗2.7 | G P a \mathrm{GPa} GPa |
| ρ \rho ρ | 2.7 2.7 2.7 | g / c m 3 \mathrm{g/cm^3} g/cm3 |
首先我们定义一下所需要使用的变量
import numpy as np
import matplotlib.pyplot as plt
import time
## parameters
xmin, xmax = 0, 1280
zmin, zmax = 0, 1280
tmin, tmax = 0, 0.2
dx, dz, dt = 5, 5, 2e-4
fm = 40
nt = int(tmax / dt)
nx = int((xmax - xmin) / dx)
nz = int((zmax - zmin) / dz)
c11 = 3000 ** 2 * 2.7 * np.ones((nz, nx))
c12 = 1500 ** 2 * 2.7 * np.ones((nz, nx))
c44 = (c11 - c12) / 2
rho = 2.7 * np.ones((nz, nx))
kx = cal_psm_k(nx, 2 * np.pi / (dx * nx))
kz = cal_psm_k(nz, 2 * np.pi / (dx * nx))
meidum_shape = np.asarray([nz, nx])
ux = np.zeros(shape=meidum_shape)
uz = np.zeros(shape=meidum_shape)
lux = np.zeros(shape=meidum_shape)
luz = np.zeros(shape=meidum_shape)
current_t = 0
start_time = time.time()
在空间域, 使用伪谱法处理:
def cal_psm_k(n, k):
res = np.array(
[i if i <= n / 2 else i - n for i in range(n)]
) * k
return res
def cal_dx(u, kx):
return np.real(np.fft.ifft2(1j * kx * np.fft.fft2(u)))
def cal_ddx(u, kx):
return np.real(np.fft.ifft2(-kx ** 2 * np.fft.fft2(u)))
def cal_dz(u, kz):
return np.real(np.fft.ifft2(1j * kz * np.fft.fft2(u.T))).T
def cal_ddz(u, kz):
return np.real(np.fft.ifft2(-kz ** 2 * np.fft.fft2(u.T))).T
对于(1)式中的 A \mathbf{A} A, 我们定义如下函数计算:
def calculate_step_value(ux, uz):
return np.asarray(
[
c11 * cal_ddx(ux, kx) +
(c12 + c44) * cal_dz(cal_dx(uz, kx), kz) +
c44 * cal_ddz(ux, kz),
c11 * cal_ddz(uz, kz) +
(c12 + c44) * cal_dz(cal_dx(ux, kx), kz) +
c44 * cal_ddx(uz, kx)
]
)
在时间域,我们使用有限差分处理:
def time_fd2(field_now, field_last, dt, time_factor):
tmp = field_now
field_now = 2 * field_now - field_last + dt**2 * time_factor
field_last = tmp
return field_now, field_last
于是,一次迭代就可以用如下代码进行求解:
(ux, uz), (lux, luz) = time_fd2(
np.asarray([ux, uz]),
np.asarray([lux, luz]),
dt,
1 / rho * calculate_step_value(ux, uz)
)
接下来增加震源, 选用雷克子波:
def ricker(t):
return (1 - 2 * (np.pi * fm * (t - dt)) ** 2) * np.exp(-(fm * np.pi * (t - dt)) ** 2)
最后将每一次迭代的结果成图:
def plot_frame_xz(datax, dataz, fig, t, *args, **kwargs):
fig.suptitle(f"t={t:.2f}s")
plt.subplot(121)
plot_frame(datax, *args, **kwargs)
plt.title("X")
plt.subplot(122)
plot_frame(dataz, *args, **kwargs)
plt.title("Z")
于是一次模拟就可以用如下代码实现:
current_t = 0
for i in range(nt):
ux[source_index_z][source_index_x] += ricker(current_t)
uz[source_index_z][source_index_x] += ricker(current_t)
(ux, uz), (lux, luz) = time_fd2(
np.asarray([ux, uz]),
np.asarray([lux, luz]),
dt,
1 / rho * calculate_step_value(ux, uz)
)
print("\rSimulation Process: time:{:.3f}s, runtime:{:.3f}s".format(current_t, time.time() - start_time),
end="")
if i % 50 == 0:
plot_frame_xz(
ux,
uz,
fig,
current_t,
vmin=-np.percentile(ux, 99) * 5,
vmax= np.percentile(ux, 99) * 5,
extent=[xmin, xmax, zmax, zmin],
)
plt.pause(0.1)
plt.cla()
plt.clf()
current_t += dt
下面是完整代码:
import time
import numpy as np
import matplotlib.pyplot as plt
def ricker(t):
return (1 - 2 * (np.pi * fm * (t - dt)) ** 2) * np.exp(-(fm * np.pi * (t - dt)) ** 2)
def cal_psm_k(n, k):
res = np.array(
[i if i <= n / 2 else i - n for i in range(n)]
) * k
return res
def cal_dx(u, kx):
return np.real(np.fft.ifft2(1j * kx * np.fft.fft2(u)))
def cal_ddx(u, kx):
return np.real(np.fft.ifft2(-kx ** 2 * np.fft.fft2(u)))
def cal_dz(u, kz):
return np.real(np.fft.ifft2(1j * kz * np.fft.fft2(u.T))).T
def cal_ddz(u, kz):
return np.real(np.fft.ifft2(-kz ** 2 * np.fft.fft2(u.T))).T
def calculate_step_value(ux, uz):
return np.asarray(
[
c11 * cal_ddx(ux, kx) +
(c12 + c44) * cal_dz(cal_dx(uz, kx), kz) +
c44 * cal_ddz(ux, kz),
c11 * cal_ddz(uz, kz) +
(c12 + c44) * cal_dz(cal_dx(ux, kx), kz) +
c44 * cal_ddx(uz, kx)
]
)
def time_fd2(field_now, field_last, dt, time_factor):
tmp = field_now
field_now = 2 * field_now - field_last + dt**2 * time_factor
field_last = tmp
return field_now, field_last
def plot_frame(data, *args, **kwargs):
kwargs.setdefault('cmap', 'seismic')
kwargs.setdefault('aspect', 'auto')
return plt.imshow(
data,
*args,
**kwargs,
)
def plot_frame_xz(datax, dataz, fig, t, *args, **kwargs):
fig.suptitle(f"t={t:.2f}s")
plt.subplot(121)
plot_frame(datax, *args, **kwargs)
plt.title("X")
plt.subplot(122)
plot_frame(dataz, *args, **kwargs)
plt.title("Z")
## parameters
xmin, xmax = 0, 1280
zmin, zmax = 0, 1280
tmin, tmax = 0, 0.2
dx, dz, dt = 5, 5, 2e-4
fm = 40
nt = int(tmax / dt)
nx = int((xmax - xmin) / dx)
nz = int((zmax - zmin) / dz)
c11 = 3000 ** 2 * 2.7 * np.ones((nz, nx))
c12 = 1500 ** 2 * 2.7 * np.ones((nz, nx))
c44 = (c11 - c12) / 2
rho = 2.7 * np.ones((nz, nx))
kx = cal_psm_k(nx, 2 * np.pi / (dx * nx))
kz = cal_psm_k(nz, 2 * np.pi / (dx * nx))
meidum_shape = np.asarray([nz, nx])
ux = np.zeros(shape=meidum_shape)
uz = np.zeros(shape=meidum_shape)
lux = np.zeros(shape=meidum_shape)
luz = np.zeros(shape=meidum_shape)
current_t = 0
start_time = time.time()
fig = plt.figure(figsize=(9, 4), dpi=120)
source_index_x = nx // 2
source_index_z = nz // 2
for i in range(nt):
ux[source_index_z][source_index_x] += ricker(current_t)
uz[source_index_z][source_index_x] += ricker(current_t)
(ux, uz), (lux, luz) = time_fd2(
np.asarray([ux, uz]),
np.asarray([lux, luz]),
dt,
1 / rho * calculate_step_value(ux, uz)
)
print("\rSimulation Process: time:{:.3f}s, runtime:{:.3f}s".format(current_t, time.time() - start_time),
end="")
if i % 50 == 0:
plot_frame_xz(
ux,
uz,
fig,
current_t,
vmin=-np.percentile(ux, 99) * 5,
vmax= np.percentile(ux, 99) * 5,
extent=[xmin, xmax, zmax, zmin],
)
plt.pause(0.1)
plt.cla()
plt.clf()
current_t += dt
使用伪谱法模拟的结果如下:
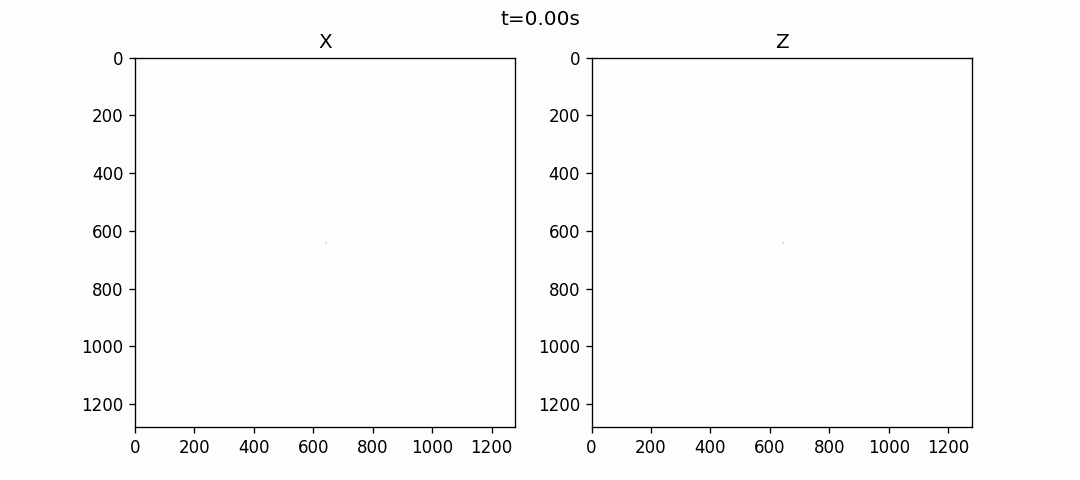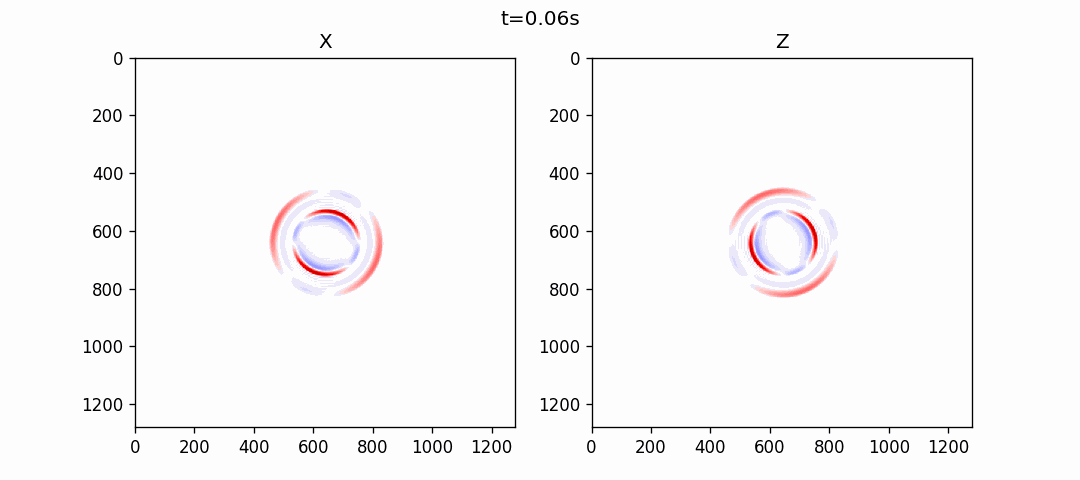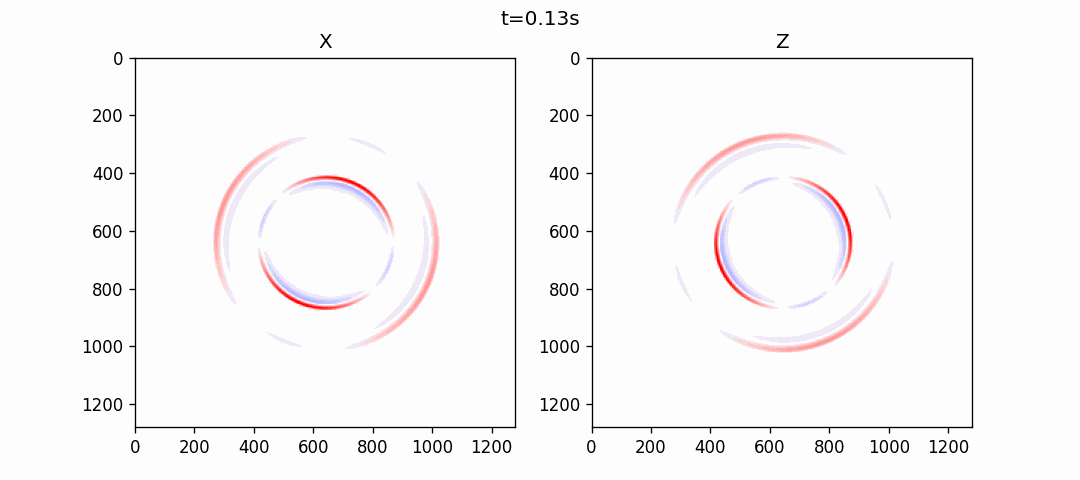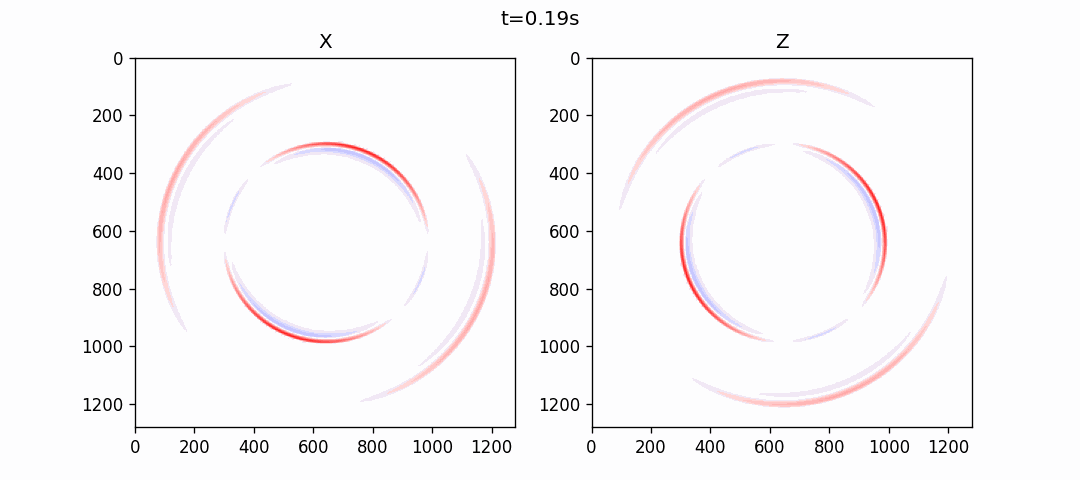
各向异性介质伪谱法模拟
这部分其实与各向同性介质一样,只是弹性系数矩阵发生了改变,因此只需要更改一下计算 A \mathbf{A} A 的方程即可。需要运行可以直接去我的github上下载运行 Github项目链接(https://github.com/Sumbrella/Seismic-Wave-Simulation)。