目录
1.单向不带头链表
1.1 链表的概念及结构
1.2 代码部分
1.3 完整的全部代码
2. 双向不带头链表
2.1 代码部分
2.2 完整的代码
3. MySingleList与MyLinkedList代码上的区别
4. LinkedList的使用
4.1 什么是LinkedList
4.2 LinkedList的使用
4.2.1 LinkedList的构造
4.2.2 LinkedList的其他常用方法介绍
4.2.3 LinkedList的遍历
5. ArrayList和LinkedList的区别
1.单向不带头链表
1.1 链表的概念及结构
链表是一种物理存储结构上非连续存储结构,数据元素的逻辑顺序是通过链表中的引用链接次序实现的 。
类似于火车
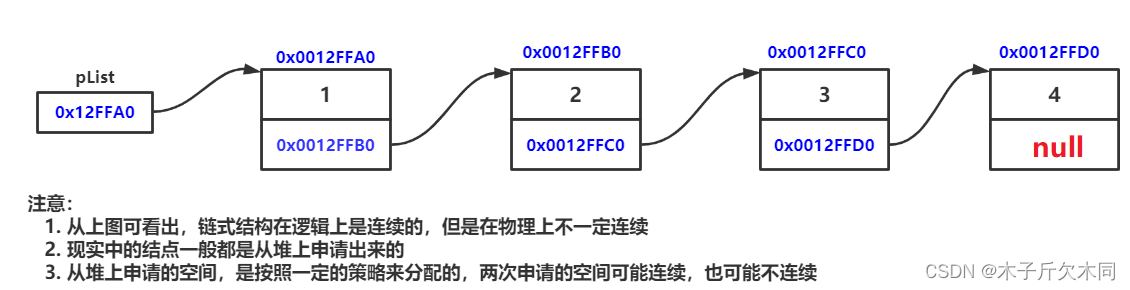
实际中链表的结构非常多样,以下情况组合起来就有8种链表结构:
(1)单向或双向

(2)带头或者不带头

(3) 循环或者非循环
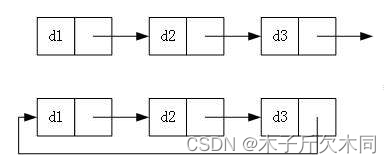
虽然有这么多的链表的结构,但是我们重点掌握两种:
- 无头单向非循环链表:结构简单,一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构,如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。
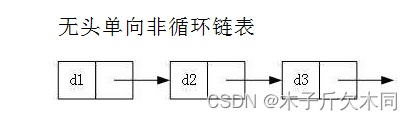
- 无头双向链表:在Java的集合框架库中LinkedList底层实现就是无头双向循环链表。
1.2 代码部分
不带头单向链表MySingleList
(1)包含了不带头单向链表的属性,用内部类去定义
(2)用方法定义该链表的操作
链表命名如下:
public class MySinglelist {…}(1)用静态内部类定义节点的属性(注:Java中的引用类型的变量存储都是地址)
static class ListNode{
public int val;//存储的数据
public ListNode next;//存储下一个节点的地址
//定义一个内部类的构造方法
public ListNode(int val){
this.val = val;
}
}
(2)代表当前链表的头结点引用
public ListNode head;(3)为了测试方便,先直接创建3个结点,且添加到链表中,这个方法很少用到的
public void createLink(){
ListNode listNode1 = new ListNode(1);
ListNode listNode2 = new ListNode(2);
ListNode listNode3 = new ListNode(3);
ListNode listNode4 = new ListNode(4);
head = listNode1;
listNode1.next = listNode2;
listNode2.next = listNode3;
listNode3.next = listNode4;
}(4)从头开始遍历
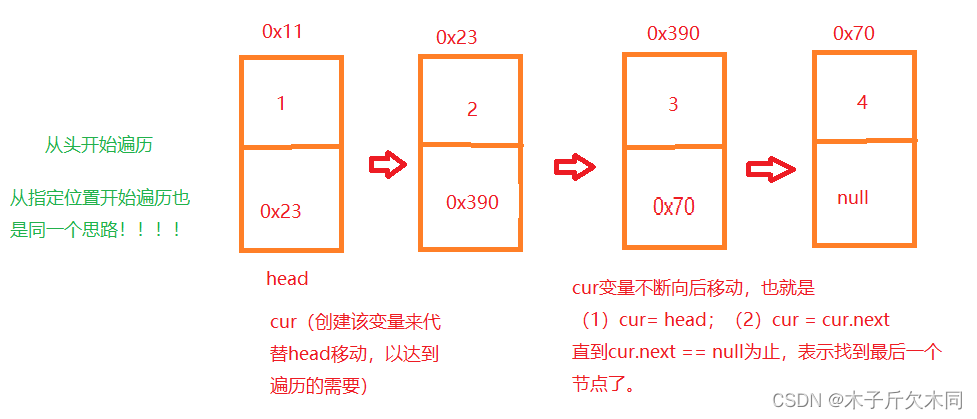
public void display(){
if(head == null)
return;
//创建一个变量cur来代表head移动
ListNode cur = head;
while(cur != null){
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();
}(5)从指定位置开始遍历
//从指定位置遍历
public void display(ListNode newHead){
//如果说 把整个链表 遍历完成 那么 就需要 head == null
// 如果说 你遍历到链表的尾巴 head.next == null
ListNode cur = newHead;
while(cur != null){
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();
}(6)查找是否包含关键字可以是否在单链表当中
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key){
ListNode cur = head;
//思路:要遍历所有节点
while(cur != null){
//然后去比较是否包含这个值,是就返回true,
if(cur.val == key)
return true;
cur = cur.next;
}
//当跳出循环后,还没有找到key,意味着没找到,返回false
return false;
}(7)得到单链表的长度,时间复杂度O(N)
//得到单链表的长度,时间复杂度O(N)
public int size(){
ListNode cur = head;
int count = 0;
while(cur != null){
count++;
cur = cur.next;
}
return count;
}(8)头插法,时间复杂度O(1)
//头插法 O(1)
public void addFirst(int data){
ListNode listNode = new ListNode(data);
listNode.next = head;
head = listNode;
}(9)尾插法,时间复杂度O(N),注:其实就是找尾巴的过程
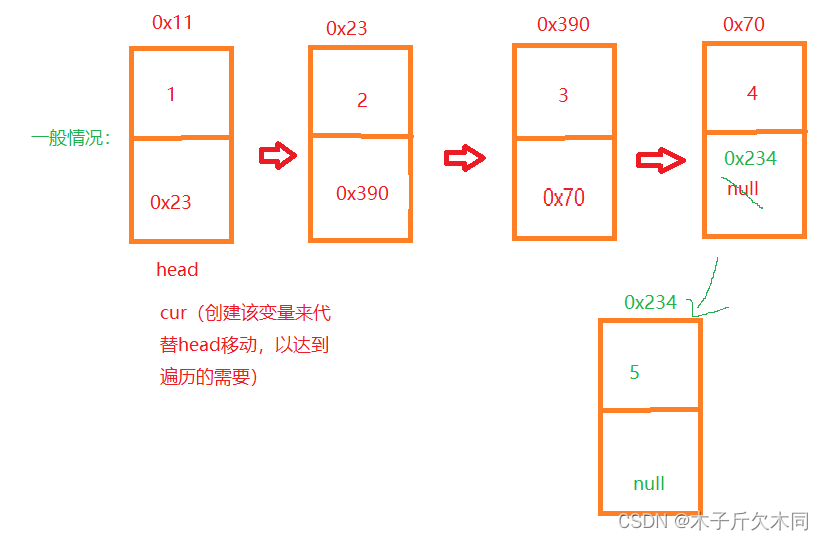
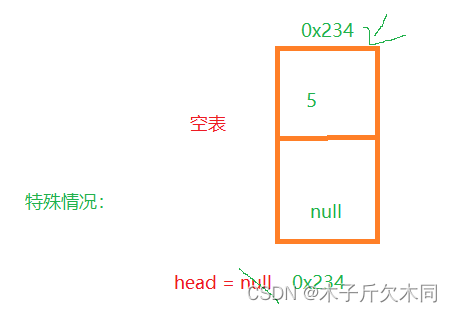
//尾插法 O(N),注:就是找尾巴的过程
public void addLast(int data){
ListNode listNode = new ListNode(data);
//处理特殊情况:空表的情况,那么直接将listNode赋值给head
if(head == null){
head = listNode;
return;
}
ListNode cur = head;
while(cur != null){
cur = cur.next;
}
cur.next = listNode;
}(10)任意位置插入,第一个数据结点为0号下标
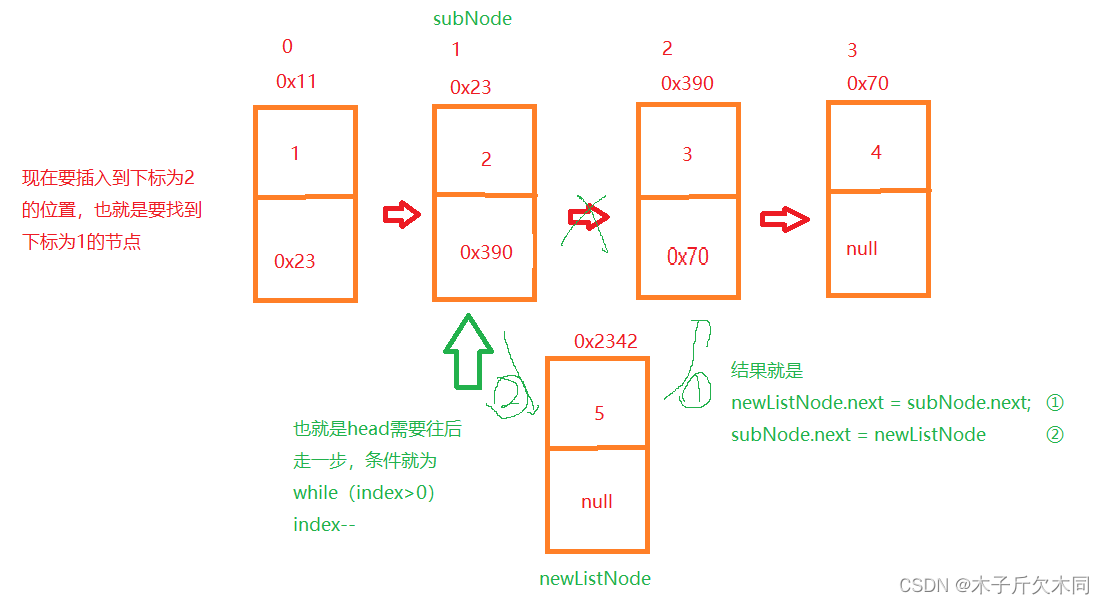
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data){
//先检查index是否合法
chechIndex(index);
//如果是index == 0,就可以用头插法
if(index == 0){
addFirst(data);
return;
}
if(index == size()){
addLast(data);
return;
}
ListNode newListNode = new ListNode(data);
ListNode subNode = findIndexSubOne(index);
newListNode.next = subNode.next;//把原subNode后一个节点地址给newListNode的next域
subNode.next = newListNode;//把新节点接在sub后面
}
//检查下标是否合法
//因为是类里面自己调用,所以不需要用public修饰
private void chechIndex(int index) throws ListIndexOutOfException{
if(index < 0 || index > size()){
throw new ListIndexOutOfException();
}
}
//找到index下标的前一个节点,也就是index - 1的节点
private ListNode findIndexSubOne(int index){
ListNode cur = head;
while(index > 1){
cur = cur.next;
index--;
}
return cur;
}(11)删除第一次出现关键字为key的节点 O(N)
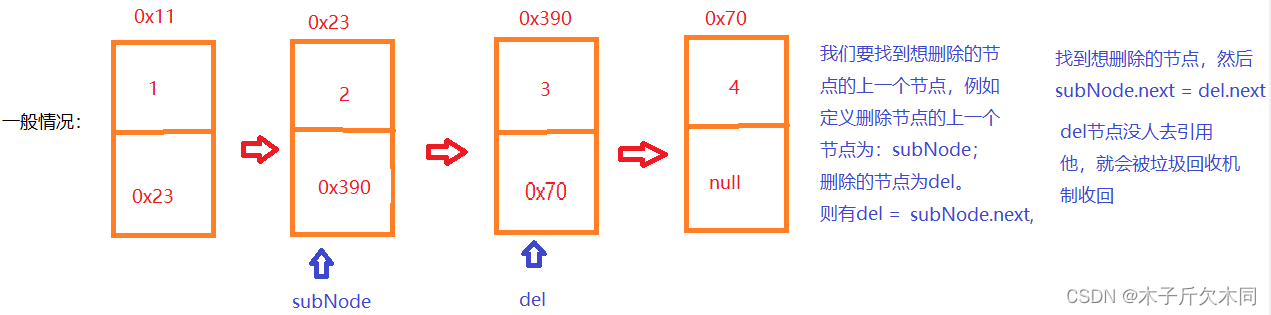

//删除第一次出现关键字为key的节点 O(N)
public void remove(int key){
//特殊情况:一个节点都没有
if(head == null){
return;
}
//通常情况
//首先,当我找到了key的节点,要删除该节点,需要知道上一个节点
//如果只有一个节点且key == head.key,那么head.next = null
if(head.val == key){
head = head.next;
return;
}
//找到删除节点的前一个节点
ListNode subNode = searchPrev(key);
//该if代码是为了防止空指针异常(当没找到key的节点就会导致空指针异常)
if(subNode == null){
return;
}
ListNode del = subNode.next;//要删除的节点
subNode.next = del.next;
}
//找到关键字key的前一个节点
//因为是类内自己使用,所以使用private修饰符
private ListNode searchPrev(int key){
ListNode cur = head;
while(cur.next != null){
if(cur.next.val == key)
return cur;
cur = cur.next;
}
return null;//没有你要删除的结点,所以没有上一个节点
}(12)删除所有值为key的节点
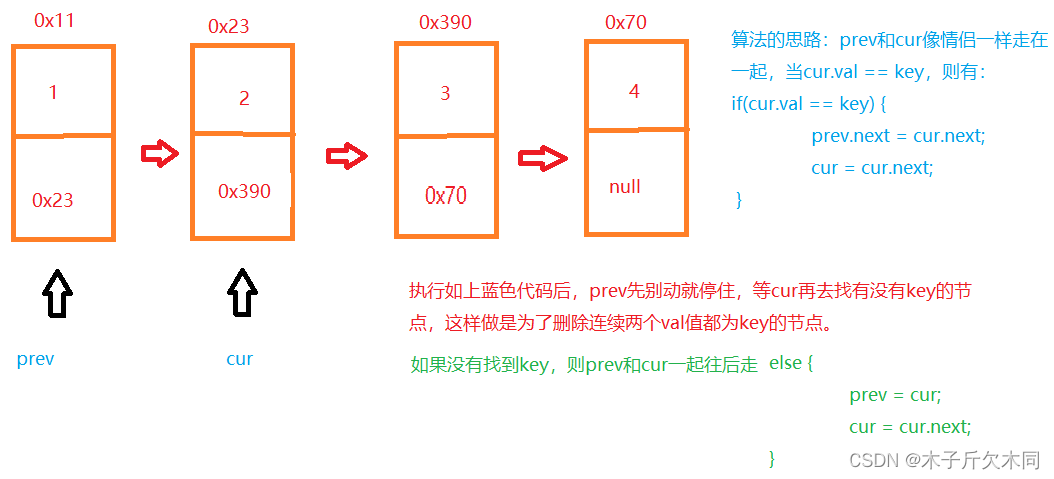
//删除所有制为key的节点
public void removeAllkey(int key){
if(head == null){
return;
}
ListNode prev = head;
ListNode cur = head.next;
while(cur != null){
if(cur.val == key){
prev.next = cur.next;
cur = cur.next;
}else{
cur = cur.next;
prev = prev.next;
}
}
//最后处理第一个节点
if(head.val == key){
head = head.next;
}
}(13)保证链表当中所有的节点,都可以被回收
/**
* 保证链表当中 所有的节点 都可以被回收
*/
public void clear(){
//当head节点没有指向,其余节点都会被gc回收
head = null;
}1.3 完整的全部代码
/*
不带头单向链表
MySingleList
(1)包含了不带头单向链表的属性,用内部类去定义
(2)用方法定义该链表的操作
*/
public class MySinglelist {
//用静态内部类定义节点的属性
/*
java中的引用类型的变量存储都是地址
*/
static class ListNode{
public int val;//存储的数据
public ListNode next;//存储下一个节点的地址
//定义一个内部类的构造方法
public ListNode(int val){
this.val = val;
}
}
//代表当前链表的头结点的引用
public ListNode head;
//创建3个节点,且添加到链表中,这个方法很少用到
public void createLink(){
ListNode listNode1 = new ListNode(1);
ListNode listNode2 = new ListNode(2);
ListNode listNode3 = new ListNode(3);
ListNode listNode4 = new ListNode(4);
head = listNode1;
listNode1.next = listNode2;
listNode2.next = listNode3;
listNode3.next = listNode4;
}
//从头开始遍历
public void display(){
if(head == null)
return;
//创建一个变量cur来代表head移动
ListNode cur = head;
while(cur != null){
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();
}
//从指定位置遍历
public void display(ListNode newHead){
//如果说 把整个链表 遍历完成 那么 就需要 head == null
// 如果说 你遍历到链表的尾巴 head.next == null
ListNode cur = newHead;
while(cur != null){
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();
}
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key){
ListNode cur = head;
//思路:要遍历所有节点
while(cur != null){
//然后去比较是否包含这个值,是就返回true,
if(cur.val == key)
return true;
cur = cur.next;
}
//当跳出循环后,还没有找到key,意味着没找到,返回false
return false;
}
//得到单链表的长度,时间复杂度O(N)
public int size(){
ListNode cur = head;
int count = 0;
while(cur != null){
count++;
cur = cur.next;
}
return count;
}
//头插法 O(1)
public void addFirst(int data){
ListNode listNode = new ListNode(data);
listNode.next = head;
head = listNode;
}
//尾插法 O(N),注:就是找尾巴的过程
public void addLast(int data){
ListNode listNode = new ListNode(data);
//处理特殊情况:空表的情况,那么直接将listNode赋值给head
if(head == null){
head = listNode;
return;
}
ListNode cur = head;
while(cur != null){
cur = cur.next;
}
cur.next = listNode;
}
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data){
//先检查index是否合法
chechIndex(index);
//如果是index == 0,就可以用头插法
if(index == 0){
addFirst(data);
return;
}
if(index == size()){
addLast(data);
return;
}
ListNode newListNode = new ListNode(data);
ListNode subNode = findIndexSubOne(index);
newListNode.next = subNode.next;//把原subNode后一个节点地址给newListNode的next域
subNode.next = newListNode;//把新节点接在sub后面
}
//检查下标是否合法
//因为是类里面自己调用,所以不需要用public修饰
private void chechIndex(int index) throws ListIndexOutOfException{
if(index < 0 || index > size()){
throw new ListIndexOutOfException();
}
}
//找到index下标的前一个节点,也就是index - 1的节点
private ListNode findIndexSubOne(int index){
ListNode cur = head;
while(index > 1){
cur = cur.next;
index--;
}
return cur;
}
//删除第一次出现关键字为key的节点 O(N)
public void remove(int key){
//特殊情况:一个节点都没有
if(head == null){
return;
}
//通常情况
//首先,当我找到了key的节点,要删除该节点,需要知道上一个节点
//如果只有一个节点且key == head.key,那么head.next = null
if(head.val == key){
head = head.next;
return;
}
//找到删除节点的前一个节点
ListNode subNode = searchPrev(key);
//该if代码是为了防止空指针异常(当没找到key的节点就会导致空指针异常)
if(subNode == null){
return;
}
ListNode del = subNode.next;//要删除的节点
subNode.next = del.next;
}
//找到关键字key的前一个节点
//因为是类内自己使用,所以使用private修饰符
private ListNode searchPrev(int key){
ListNode cur = head;
while(cur.next != null){
if(cur.next.val == key)
return cur;
cur = cur.next;
}
return null;//没有你要删除的结点,所以没有上一个节点
}
//删除所有制为key的节点
public void removeAllkey(int key){
if(head == null){
return;
}
ListNode prev = head;
ListNode cur = head.next;
while(cur != null){
if(cur.val == key){
prev.next = cur.next;
cur = cur.next;
}else{
cur = cur.next;
prev = prev.next;
}
}
//最后处理第一个节点
if(head.val == key){
head = head.next;
}
}
/**
* 保证链表当中 所有的节点 都可以被回收
*/
public void clear(){
//当head节点没有指向,其余节点都会被gc回收
head = null;
}
}2. 双向不带头链表
2.1 代码部分
(1)把结点包装起来,采用了内部类的方法
//把结点包装起来
static class ListNode{
public int val;
public ListNode prev;//前驱
public ListNode next;//后继
public ListNode(int val){
this.val = val;
}
}(2)定义指向头部和尾部的指针
//定义指向头部和尾部的指针
public ListNode head;
public ListNode last;(3)遍历整个表
public void display(){
ListNode cur = head;
while(cur != null){
System.out.println(cur.val + " ");
cur = cur.next;
}
System.out.println();
}(4) 头插法 O(1)
//头插法 O(1)
public void addFirst(int data){
//先创建一个结点
ListNode newNode = new ListNode(data);
//判断原来是否为空表
if(head == null){
head = newNode;
last = newNode;
}else{//原表有数据,往里面添加数据
newNode.next = head;
head.prev = newNode;
head = newNode;
}
}
(5)尾插法 O(1)
//尾插法 O(1)
public void addLast(int data){
ListNode newNode = new ListNode(data);
//判断原来是否为空表
if(head == null){
head = newNode;
last = newNode;
}else{//原表有数据,往里面添加数据
last.next = newNode;
newNode.prev = last;
last = newNode;
}
}
(6)任意位置插入,第一个数据节点为0号下标
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data){
//先判断index是否合法
if(index < 0 || index > size()){
throw new ListIndexOutOfException("index不合法");
}
//如果index为0,调用头插法
if(index == 0){
addFirst(data);
return;
}
//如果index为size(),调用尾插法
if(index == size()){
addLast(data);
return;
}
//在其他位置进行插入
//先找到插入结点的位置
ListNode cur = findIndex(index);
//创建一个新的结点
ListNode newNode = new ListNode(data);
//进行插入
newNode.next = cur;
cur.prev.next = newNode;
newNode.next = cur;
cur.prev = newNode;
}(7)找到插入结点的位置
//找到插入结点的位置
private ListNode findIndex(int index){
ListNode cur = head;
while(index > 0){
cur = cur.next;
index--;
}
return cur;
}(8)计算大小
//计算大小
public int size(){
int count = 0;
ListNode cur = head;
while(cur != null){
count++;
cur = cur.next;
}
return count;
}(9)查找是否包含关键字key是否在单链表当中
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key){
ListNode cur = head;//作为代步滴滴
while(cur != null){
if (cur.val == key){
return true;
}
cur = cur.next;
}
return false;
}(10)删除第一次出现关键字为key的节点
//删除第一次出现关键字为key的节点
public void remove(int key){
ListNode cur = head;
while (cur != null){
//开始删除
if(cur.val == key){
//1. 如果删除的是第一个结点
if(head.val == key){
head = head.next;
//1.1 如果不是只有一个结点的时候
//才可以将前驱结点做空
if(head != null){
head.prev = null;
}
}else{//2. 如果删除的是其他结点
//中间结点
cur.prev.next = cur.next;
//cur.next.prev = cur.prev;cur指向的是尾结点,cur.next.prev 就会发生空指针异常
//所以需要当不是尾结点时,才能执行这段代码
if(cur.next != null){
cur.next.prev = cur.prev;
}else{//如果是尾巴结点
last = last.prev;
}
}
return;//如果是删除一个结点就多了个return
}
cur = cur.next;
}
}(11)删除所有值为key的节点
//删除所有值为key的节点
public void removeAllKey(int key){
ListNode cur = head;
while (cur != null){
//开始删除
if(cur.val == key){
//1. 如果删除的是第一个结点
if(head.val == key){
head = head.next;
//1.1 如果不是只有一个结点的时候
//才可以将前驱结点做空
if(head != null){
head.prev = null;
}
}else{//2. 如果删除的是其他结点
//中间结点
cur.prev.next = cur.next;
//cur.next.prev = cur.prev;cur指向的是尾结点,cur.next.prev 就会发生空指针异常
//所以需要当不是尾结点时,才能执行这段代码
if(cur.next != null){
cur.next.prev = cur.prev;
}else{//如果是尾巴结点
last = last.prev;
}
}
}
cur = cur.next;
}
}(12)保证链表当中所有的节点,都可以被回收
public void clear(){
/*ListNode cur = head;
while (cur != null) {
ListNode curNext = cur.next;
cur.prev = null;
cur.next = null;
cur = curNext;
}*/
head = null;
last = null;
}2.2 完整的代码
public class MyLinkedList {
//把结点包装起来
static class ListNode{
public int val;
public ListNode prev;//前驱
public ListNode next;//后继
public ListNode(int val){
this.val = val;
}
}
//定义指向头部和尾部的指针
public ListNode head;
public ListNode last;
//遍历整个表
public void display(){
ListNode cur = head;
while(cur != null){
System.out.println(cur.val + " ");
cur = cur.next;
}
System.out.println();
}
//头插法 O(1)
public void addFirst(int data){
//先创建一个结点
ListNode newNode = new ListNode(data);
//判断原来是否为空表
if(head == null){
head = newNode;
last = newNode;
}else{//原表有数据,往里面添加数据
newNode.next = head;
head.prev = newNode;
head = newNode;
}
}
//尾插法 O(1)
public void addLast(int data){
ListNode newNode = new ListNode(data);
//判断原来是否为空表
if(head == null){
head = newNode;
last = newNode;
}else{//原表有数据,往里面添加数据
last.next = newNode;
newNode.prev = last;
last = newNode;
}
}
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index,int data){
//先判断index是否合法
if(index < 0 || index > size()){
throw new ListIndexOutOfException("index不合法");
}
//如果index为0,调用头插法
if(index == 0){
addFirst(data);
return;
}
//如果index为size(),调用尾插法
if(index == size()){
addLast(data);
return;
}
//在其他位置进行插入
//先找到插入结点的位置
ListNode cur = findIndex(index);
//创建一个新的结点
ListNode newNode = new ListNode(data);
//进行插入
newNode.next = cur;
cur.prev.next = newNode;
newNode.next = cur;
cur.prev = newNode;
}
//找到插入结点的位置
private ListNode findIndex(int index){
ListNode cur = head;
while(index > 0){
cur = cur.next;
index--;
}
return cur;
}
//计算大小
public int size(){
int count = 0;
ListNode cur = head;
while(cur != null){
count++;
cur = cur.next;
}
return count;
}
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key){
ListNode cur = head;//作为代步滴滴
while(cur != null){
if (cur.val == key){
return true;
}
cur = cur.next;
}
return false;
}
//删除第一次出现关键字为key的节点
public void remove(int key){
ListNode cur = head;
while (cur != null){
//开始删除
if(cur.val == key){
//1. 如果删除的是第一个结点
if(head.val == key){
head = head.next;
//1.1 如果不是只有一个结点的时候
//才可以将前驱结点做空
if(head != null){
head.prev = null;
}
}else{//2. 如果删除的是其他结点
//中间结点
cur.prev.next = cur.next;
//cur.next.prev = cur.prev;cur指向的是尾结点,cur.next.prev 就会发生空指针异常
//所以需要当不是尾结点时,才能执行这段代码
if(cur.next != null){
cur.next.prev = cur.prev;
}else{//如果是尾巴结点
last = last.prev;
}
}
return;//如果是删除一个结点就多了个return
}
cur = cur.next;
}
}
//删除所有值为key的节点
public void removeAllKey(int key){
ListNode cur = head;
while (cur != null){
//开始删除
if(cur.val == key){
//1. 如果删除的是第一个结点
if(head.val == key){
head = head.next;
//1.1 如果不是只有一个结点的时候
//才可以将前驱结点做空
if(head != null){
head.prev = null;
}
}else{//2. 如果删除的是其他结点
//中间结点
cur.prev.next = cur.next;
//cur.next.prev = cur.prev;cur指向的是尾结点,cur.next.prev 就会发生空指针异常
//所以需要当不是尾结点时,才能执行这段代码
if(cur.next != null){
cur.next.prev = cur.prev;
}else{//如果是尾巴结点
last = last.prev;
}
}
}
cur = cur.next;
}
}
public void clear(){
/*ListNode cur = head;
while (cur != null) {
ListNode curNext = cur.next;
cur.prev = null;
cur.next = null;
cur = curNext;
}*/
head = null;
last = null;
}
}3. MySingleList与MyLinkedList代码上的区别
| 最大区别 | MySingleList | MyLinkedList |
| 删除结点 | 需要找到想删除结点的上一个结点 | 不需要找到删除结点的上一个结点,只需要找到想删除的结点 |
4. LinkedList的使用
4.1 什么是LinkedList
LinkedList的官方文档
LinkedList的底层是双向链表结构(链表后面介绍),由于链表没有将元素存储在连续的空间中,元素存储在单独的节点中,然后通过引用将节点连接起来了,因此在在任意位置插入或者删除元素时,不需要搬移元素,效率比较高。
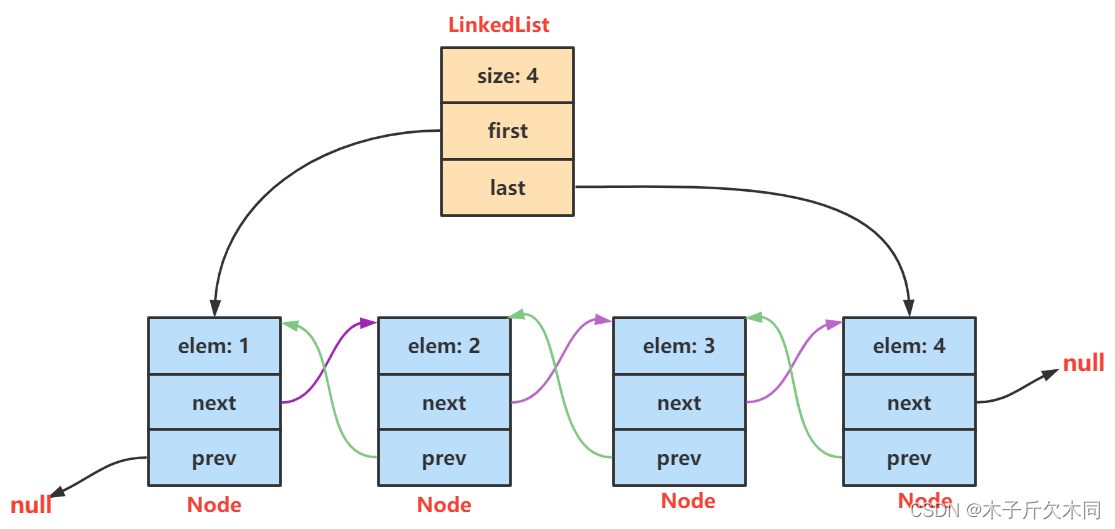
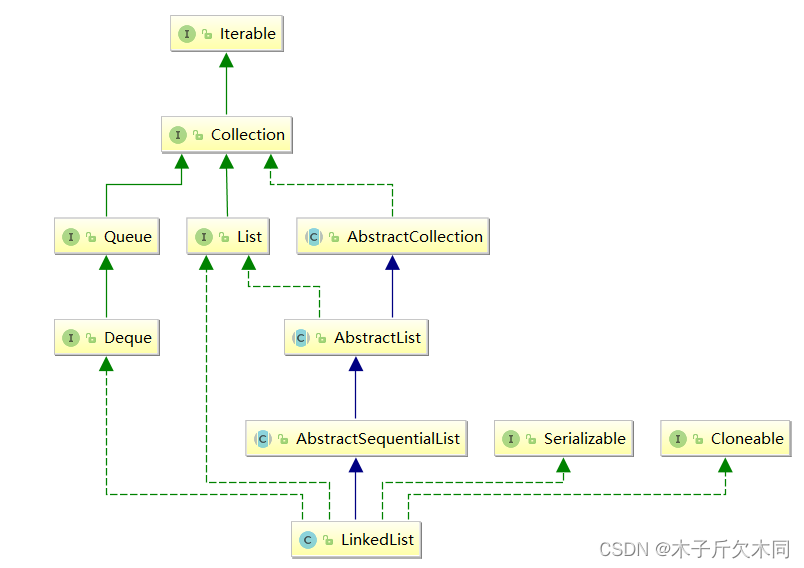
【说明】
1. LinkedList实现了List接口
2. LinkedList的底层使用了双向链表
3. LinkedList没有实现RandomAccess(该接口是实现随机访问)接口,因此LinkedList不支持随机访问
4. LinkedList的任意位置插入和删除元素时效率比较高,时间复杂度为O(1)
5. LinkedList比较适合任意位置插入的场景
4.2 LinkedList的使用
4.2.1 LinkedList的构造
| 方法 | 解释 |
| LinkedList() | 无参构造 |
| public LinkedList(Collection<? extends E> c) | 使用其他集合容器中元素构造List |
public static void main(String[] args) {
// 构造一个空的LinkedList
List<Integer> list1 = new LinkedList<>();
List<String> list2 = new java.util.ArrayList<>();
list2.add("JavaSE");
list2.add("JavaWeb");
list2.add("JavaEE");
// 使用ArrayList构造LinkedList
List<String> list3 = new LinkedList<>(list2);
}4.2.2 LinkedList的其他常用方法介绍
LinkedList的使用文档
public static void main(String[] args) {
LinkedList<Integer> list = new LinkedList<>();
list.add(1); // add(elem): 表示尾插
list.add(2);
list.add(3);
list.add(4);
list.add(5);
list.add(6);
list.add(7);
System.out.println(list.size());
System.out.println(list);
// 在起始位置插入0
list.add(0, 0); // add(index, elem): 在index位置插入元素elem
System.out.println(list);
list.remove(); // remove(): 删除第一个元素,内部调用的是removeFirst()
list.removeFirst(); // removeFirst(): 删除第一个元素
list.removeLast(); // removeLast(): 删除最后元素
list.remove(1); // remove(index): 删除index位置的元素
System.out.println(list);
// contains(elem): 检测elem元素是否存在,如果存在返回true,否则返回false
if(!list.contains(1)){
list.add(0, 1);
list.add(1);
System.out.println(list);
System.out.println(list.indexOf(1)); // indexOf(elem): 从前往后找到第一个elem的位置
System.out.println(list.lastIndexOf(1)); // lastIndexOf(elem): 从后往前找第一个1的位置
int elem = list.get(0); // get(index): 获取指定位置元素
list.set(0, 100); // set(index, elem): 将index位置的元素设置为elem
System.out.println(list);
// subList(from, to): 用list中[from, to)之间的元素构造一个新的LinkedList返回
List<Integer> copy = list.subList(0, 3);
System.out.println(list);
System.out.println(copy);
list.clear(); // 将list中元素清空
System.out.println(list.size());
}
4.2.3 LinkedList的遍历
public static void main(String[] args) {
LinkedList<Integer> list = new LinkedList<>();
list.add(1); // add(elem): 表示尾插
list.add(2);
list.add(3);
list.add(4);
list.add(5);
list.add(6);
list.add(7);
System.out.println(list.size());
// foreach遍历
for (int e:list) {
System.out.print(e + " ");
}
System.out.println();
// 使用迭代器遍历---正向遍历
ListIterator<Integer> it = list.listIterator();
while(it.hasNext()){
System.out.print(it.next()+ " ");
}
System.out.println();
// 使用反向迭代器---反向遍历
ListIterator<Integer> rit = list.listIterator(list.size());
while (rit.hasPrevious()){
System.out.print(rit.previous() +" ");
}
System.out.println();
}5. ArrayList和LinkedList的区别
| 不同点 | ArrayList | LinkedList |
| 存储空间上 | 物理上一定连续 | 逻辑上连续,但物理上不一定连续 |
| 随机访问 | 支持O(1) | 不支持:O(N) |
| 头插 | 需要搬移元素,效率低O(N) | 只需修改引用的指向,时间复杂度为O(1) |
| 插入 | 空间不够时需要扩容 | 没有容量的概念 |
| 应用场景 | 元素高效存储+频繁访问 | 任意位置插入和删除频繁 |

![[deeplearning]深度学习框架torch的概念以及数学内容](https://img-blog.csdnimg.cn/0caa9ff370494eb980da467106dc8006.png)