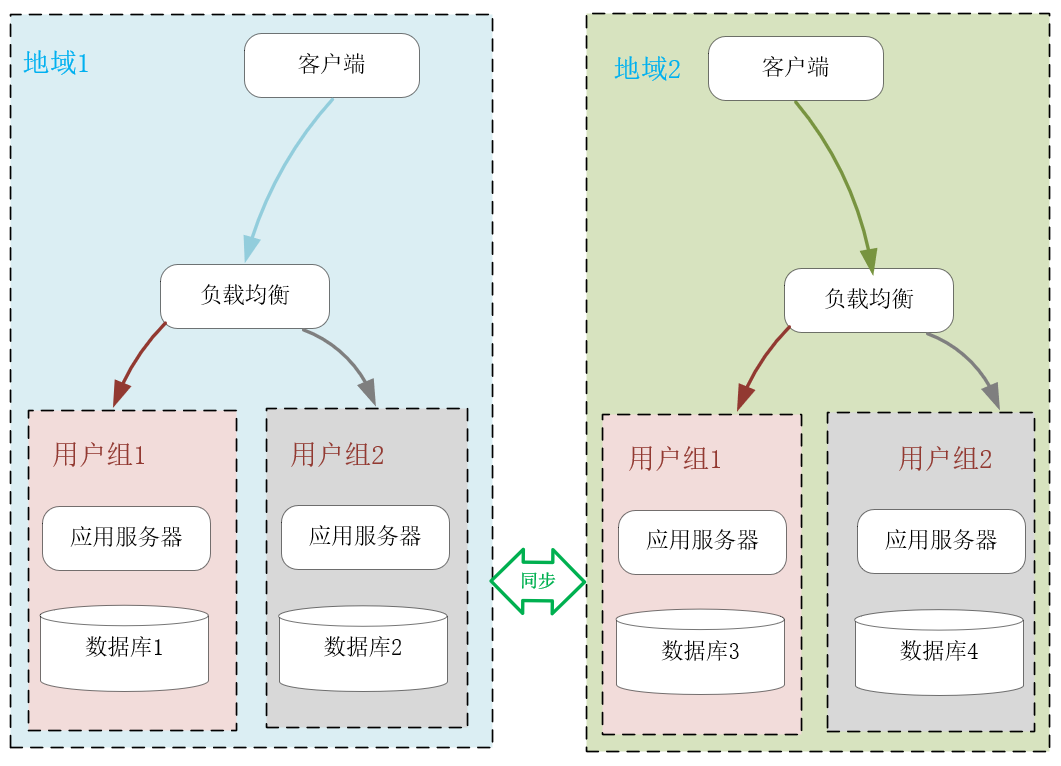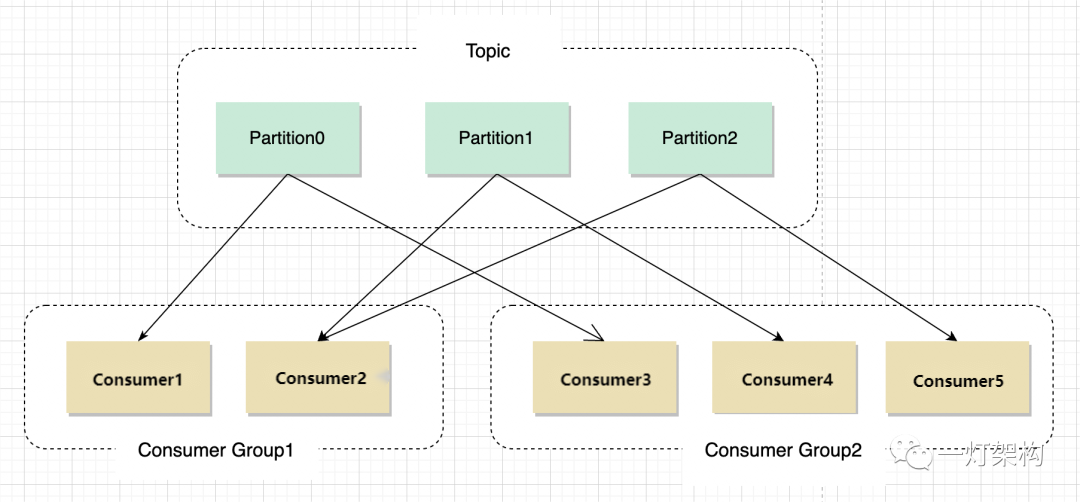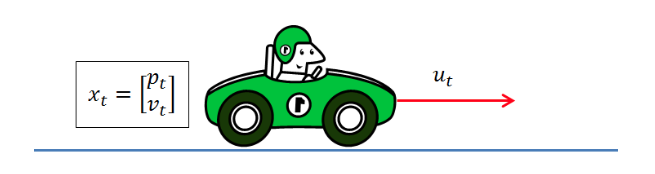
假设 小车在t时刻的初始状态可以用Pt(当前位置),Vt(当前速度),Ut表示加速度:
预测:
利用上一个时刻的旧状态和系统的动量模型(如加速度,速度等)来预测当前时刻的状态
已知上一时刻t-1时的小车状态,那么当前时刻t小车的状态可以如下表示:
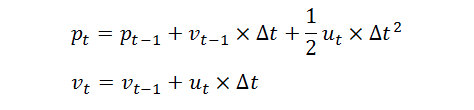
很明显上述的输入变量都是线性组合,卡尔曼滤波也被称为线性滤波器,用矩阵来表示上述公式:
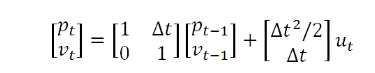
其中,
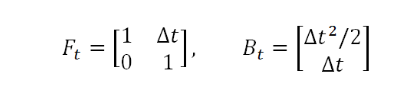
公式(二)即为状态预测方程组中的第一条公式,F为状态转移矩阵,B为控制矩阵,从公式二简化一下,得到t时刻的预测状态:

上式中x顶上的hat表示为估计值(而非真实值)。等式左端部分的右上标“-”表示该状态是根据上一状态推测而来的,稍后我们还将对其进行修正以得到最优估计,彼时才可以将“-”去掉。
考虑噪声的影响,对于一维数据进行估计时,噪声可以用其方差来表示,而多维数据来说,为了综合考虑各个维度偏离其均值的程度,需要用协方差矩阵来表示。
系统中每一个时刻的不确定性都是通过协方差矩阵 Σ 来给出的。而且这种不确定性在每个时刻间还会进行传递。也就是说不仅当前物体的状态(例如位置或者速度)是会(在每个时刻间)进行传递的,而且物体状态的不确定性也是会(在每个时刻间)进行传递的。这种不确定性的传递就可以用状态转移矩阵来表示,即(注意,这里用到了前面给出的关于协方差矩阵的性质)。

预测模型本身也并不绝对准确的,所以我们要引入一个协方差矩阵 Q 来表示预测模型本身的噪声(也即是噪声在传递过程中的不确定性

公式2即是预测状态方程组中的第二条公式,它表示不确定性在各个时刻间的传递关系
测量更新:
根据当前时刻的测量数据,利用观测矩阵和卡尔曼增益来修正预测状态
由于小车的真实状态不可知,但是我们可以得到当前时刻的观测值来对真实值进行估计。通过道路上预设的装置可以观测到小车每一个时刻的位置,观测到的值记为V(t)。而且从小汽车的真实状态到其观测状态还有一个变换关系,这个变换关系我们记为h(•),而且这个h(•)还是一个线性函数:
![]()
其中V(t)表示观测的误差。既然h(•)还是一个线性函数,所以我们同样可以把上式改写成矩阵的形式,则有:
![]()
然后,我们就可以利用上一步的预测状态来对估计的真实状态进行修正,可以得到下面公式:
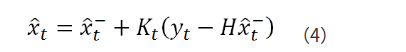
![]()
是根据上一状态推测而来的,那么它与“最优”估计值之间的差距现在就是等式右端加号右侧的部分。
![]()
表示实际观察值与预估的观测值之间的残差。这个残差再乘以一个系数K就可以用来对估计值进行修正。K称为卡尔曼系数,它也是一个矩阵,它是对残差的加权矩阵
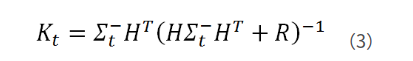
滤波增益阵首先权衡预测状态协方差矩阵Σ 和观测值矩阵R的大小,并以此来觉得我们是更倾向于相信预测模型还是详细观测模型。如果相信预测模型多一点,那么这个残差的权重就会小一点。反之亦然,如果相信观察模型多一点,这个残差的权重就会大一点。不仅如此,滤波增益阵还负责把残差的表现形式从观测域转换到了状态域。例如本题中观测值Z 仅仅是一个一维的向量,状态 x 是一个二维的向量。所以在实际应用中,观测值与状态值所采用的描述特征或者单位都有可能不同,显然直接用观测值的残差去更新状态值是不合理的。而利用卡尔曼系数,我们就可以完成这种转换。例如,在小车运动这个例子中,我们只观察到了汽车的位置,但K里面已经包含了协方差矩阵P的信息(P里面就给出了速度和位置的相关性),所以它利用速度和位置这两个维度的相关性,从位置的残差中推算出了速度的残差。从而让我们可以对状态值 x 的两个维度同时进行修正
最后需要对最优估计值的噪声分布进行更新,如下公式:
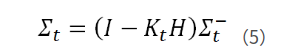
总结:

这五个公式分成预测组和更新组。
预测组总是根据前一个状态来估计当前状态;
更新组则根据观测信息来对预测信息进行修正,以期达到最优估计之目的