上篇博客中,介绍了使用KNN算法实现分类问题,本篇文章介绍使用KNN算法实现回归问题。介绍思路是先使用sklearn包提供的方法实现一个KNN算法的回归问题。再自定义实现一个KNN算法的回归问题工具类。
一、sklearn包使用KNN算法
1. 准备数据
使用sklearn包提供的make_regression模块制作回归类型数据。
from sklearn.datasets import make_regression
除了make_regession外,sklearn包还提供了制作分类问题的数据等方法,如下图:
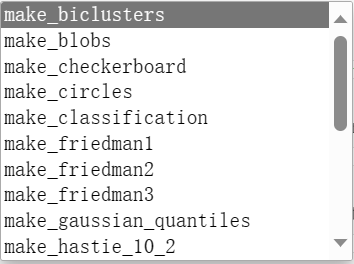
我们在需要测试数据时,可以根据需求引入不同的模块来创建数据。
生成数据:
X, y = make_regression(n_samples=10000, n_features=20, n_informative=15, random_state=0)
其中,n_samples是样本数,n_features是每个样本的特征数,n_informative是有效特征数,random_state是随机生成数的种子,种子相同,生成的X和y的值都相同。
回归问题生成的X,均值接近0,标准差接近1,是去中心化后的数据。而分类问题生成的数据,就不具有此特点,如下所示为make_regression生成的数据:
X.mean() #0.0033349709157105382
X.std() #0.998015035291231
2. 切分数据
使用sklearn提供的train_test_split方法对生成的数据进行切分:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
3. 使用sklearn包进行KNN回归问题的验证
from sklearn.neighbors import KNeighborsRegressor
# 第一步,构建模型
knn = KNeighborsRegressor(n_neighbors=7)
# 第二步,训练模型
knn.fit(X=X_train, y=y_train)
#第三步,模拟测试
y_pred = knn.predict(X =X_test)
#第四步,使用MSE评测预测结果
((y_test - y_pred)**2).mean()
首先需要知道的是,单独看最后MSE的计算结果的大小,不代表预测准确与否。而是要通过调整进邻的参数,来比较不同近邻下MSE的结果,来看选择哪个近邻参数最合适。而对于现实问题,是否要用KNN的回归问题算法来解决,是另当别论的,不能通过MSE的结果去判断是否用KNN算法正确与否。
MSE: 求预测结果与实际结果的差值的绝对值(平方),然后再求差值绝对值的平均数。具体MSE的含义和定义,参考通俗易懂讲解均方误差 (MSE)
在回归问题中,一般使用MSE表示预测结果。在分类问题中,使用预测值=实际值的平均数[(y_predict == y_test).mean()]表示预测结果。
二、自定义回归问题实现
class MyKNeighborsRegressor(object):
"""
自定义KNN 回归器
"""
def __init__(self, n_neighbors=5):
"""
挂载超参数
"""
self.n_neighbors=n_neighbors
def fit(self, X, y):
"""
训练过程
"""
self.X = np.array(X)
self.y = np.array(y)
def predict(self, X):
X = np.array(X)
results = []
for x in X:
# 计算两个向量之间的距离,sqrt((x1-x2)**2+(y1-y2)**2+......)。x是行向量,self.X是测试用例的矩阵,self.X-x用到了向量的广播机制,进行对齐然后相减。由此计算出来的距离是测试集中单个向量与训练集中所有行向量的距离
distances = ((self.X - x) ** 2).sum(axis=1)
#选出距离最近的向量的脚标
indices = distances.argsort(axis=0)[:self.n_neighbors]
#根据脚标获取训练集中的对应脚本的元素
labels = self.y[indices]
# 取距离最近的训练集的标签,然后求均值,就是回归问题的预测结果
y_pred = labels.mean()
results.append(y_pred)
return np.array(results)
三、总结
对比KNN算法的分类问题和回归问题的自定义实现,需要捋清楚几点:
- 对于上面的例子而言,样本矩阵就是一个二维数组,二维数组中的每个一维数组,就是一行,每列都代表一个特征。而一行样本数据,都会对应一个标签值,即y。
- 使用KNN算法,就是将训练数据中的样本数据和标签数据提供给模型后,在预测测试数据时,模型根据测试数据的每行样本,去查找之前提供的训练数据中所有的样本中,距离这个测试数据样本最近的n个训练样本数据。
- 找到邻近的n个训练样本数据后,找出这n个训练样本数据对应的标签值。然后在分类问题中,找出n个训练样本对应标签值中最多的那个标签,就认为是测试这条测试样本的标签值。在回归问题中,找出n个训练样本对应的标签后,求这些标签的均值,就认为是当前测试样本的标签。
- 上述是针对测试样本中每个向量的处理逻辑,当循环找出所有测试样本的标签值后,就可以返回总体的预测数据了。
- 最后通过预测数据与真实数据比对,查看是否适合用KNN算法以及近邻参数如何设置最准确。
因此,KNN算法的核心理念是通过找邻近训练样本的标签,来推算测试样本的标签进行返回。