⛲️
一、考点讲解
- 线性规划特征
线性规划是运筹学中辅助人们进行科学管理的一种数学方法。线性规划所研究的是:在一定条件下,合理安排人力物力等资源,使经济效果达到最好。一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题。 - 线性规划解题步骤
总结起来可以分三步,即“三步法”:
第一步,根据题目写出限定条件对应的不等式组;
第二步,将不等式转化为方程,解出边界交点;
第三步,若交点为整数,则直接带入目标函数求出最值。若交点不是整数,则讨论取整,然后再带入目标函数求出最值。
二、考试解读
- 这种题目的特点与管理类硕士学位对学生基本素养的要求有较高的契合度,因此近年来受到出题老师的热衷,而且此类题通常是考生的软肋,错误率极高。
- 线性规划应用题并没有使用高中阶段学习过的方法,即在平面直角坐标系内绘出可行域,再进一步利用单纯形法求得目标函数在可行域内的最值,或者求得目标函数的取值范围,这样做的原因是为了提高学生在考试中的解题速度,因为考试不是学会知识就能得高分,要同时兼备速度与准确度才能在联考中立于不败之地。
- 考试时为节省时间,可以采用简化面且有效的三步法求解。
- 考试频率级别:中。
三、命题方向
- 交点为整数点
思路如果交点为整数点,比较简单,则直接代入目标函数分析即可。 - 交点为非整数点
思路如果交点为非整数点,需要讨论其附近的两个整数,得到四个点(x有两种情况,y有两种情况),再将其中能满足要求的点代入目标函数分析即可。
【解题思路】线性规划是文字应用题的最值问题延使部分,是将定值问题转化为动态问题的过程。线性规划的含义是一次函数找最优解,难点在求最优点取整。一般情况下,可考虑可行域的端点及其附近。
🌊
最优解问题的出题模式:
题目通常会给出两种模式的解决方案,然后让我们去通过这两种模式去解决题目中涉及的问题,然后利用花费最少或者成本最少进行合理分配两种模式(线性规划)
但是,线性规划的学院派解法是通过列不等式、画图找出可行域然后进行求解,这种方法很明显在联考这种 “ 速度至上 ” 的考题中是不可取的。我们的通常解法是列出不等式,找出参数的取值范围,然后根据题意进行近似交点取值试算即可。
最优解问题套路性总结及提醒:
(1)不等式是不能相减的,但是对于最优解问题,这只是一个具有局限性的套路总结。
(2)在“ 远,近 ”和“ 便宜,贵 ”的考虑优先级上,“ 便宜,贵 ”第一优先级(优先考虑),其次才是“ 远近 ”。
(3)在最优解问题中,不建议同学们去用线性规划,可行域的套路去做,这样会非常浪费时间,在考试的时候没有可实现性。
(4)等号 - 不等号需要变号(不等号 - 等号不需要变号),注意:只变方向,而非补集。等号 + 不等号是不需要变号的,不等号 + 等号是不需要变号的。
🐟
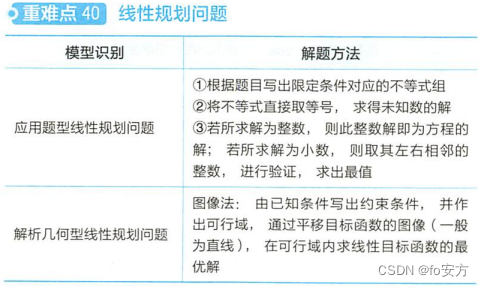
| 模型识别 | 解题方法 | 备注 |
|---|---|---|
| 应用题型线性规划问题 | ① 根据题目写出限定条件对应的不等式组; ② 将不等式直接取等号,求得未知数的解; ③ 若所求解为整数,则此整数解即为方程的解;若所求解为小数,则取其左右相邻的整数,进行验证,求出最值。 | |
| 解析几何型线性规划问题 | 图像法:由已知条件写出约束条件,并作出可行域,通过平移目标函数的图像(一般为直线),在可行域内求线性目标函数的最优解。 |
🐟——秒杀
解题方法
第一步:根据题目写出限定条件对应的不等式组。
第二步:“先看边界”,将不等式直接取等号,求得未知数的解。
第三步:“再取整数”,若所求解为整数,则此整数解即为方程的解;若所求解为小数,则取其左右相邻的整数。进行验证,求出最值。
【注意】这种方法并不严谨,但对于绝大多数选择题来说可以快速得分。
口诀:线性规划问题:先看边界再取整