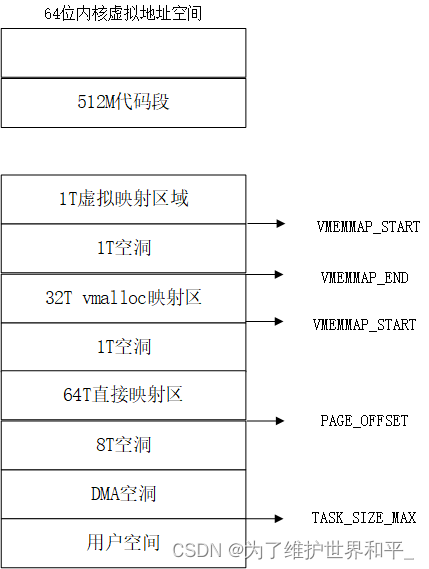
天津大学图书馆的研究馆员范铮先生,在《图书情报工作》第一期中发表了题为《原始的布拉德福定律》的文章,详细介绍了布拉德福定律的历史背景、调查统计数据、文献曲线以及理论推导等关键内容。这篇文章让我们能够深入了解布拉德福定律的本质和原始构想。(注:《原始的布拉德福定律》一文可在知网免费下载)
1934年1月英国学者布拉德福在《工程》期刊上发布了论文:Sources of Information on Specific Subjects,从大量调查统计数据中找出了文献分布与期刊出处关系的规律,使之能用数学的定量形式表示出来,即:
α : β : γ = 1 : N : N 2 α:β:γ = 1:N:N^2 α:β:γ=1:N:N2
开创性地描述了科学文献数量与科学期刊数量关系。
研究问题和结论
RQ1:布拉德福发表在《工程》上的目的
- 目的:想唤起科学技术人士对文献工作的重视
- 结果:一直到14年后,原论文《Sources of Information on Specific Subjects》被重新编入《文献工作》当中,才引起图书情报工作者的广泛重视
RQ2:布拉德福定律核心思想
- 数据源:“ 应用地球物理学 ” ,调查范围为4年(1928-1931),另一个是 “ 润滑 ”, 调查范围为2年半(1931-1933.6)。

通过对两种专题文献期刊的统计,根据图1绘出了如下示意图:

令 O X 1 = r , X 1 X 2 = S OX_1 = r, X_1X_2=S OX1=r,X1X2=S
则 X 1 X 2 = X 2 X 3 = S X_1X_2=X_2X_3=S X1X2=X2X3=S
设 α , β , γ α, β, γ α,β,γ 分别为对数横坐标的自然数,
则 l o g a = r loga=r loga=r 或 a = 1 0 r a=10^r a=10r
l o g β = r + s logβ = r+s logβ=r+s 或 β = 1 0 r × 1 0 s β=10^r × 10^s β=10r×10s
l o g γ = r + 2 s logγ = r+2s logγ=r+2s 或 γ = 1 0 r + 2 s = 1 0 r + ( 1 0 s ) 2 γ=10^{r+2s} = 10^r+(10^s)^2 γ=10r+2s=10r+(10s)2
设 1 0 s = n 10^s=n 10s=n
则: α : β : γ = 1 : n : n 2 α:β:γ = 1:n:n^2 α:β:γ=1:n:n2
- 原文文字描述:如果将有关某主题领域内的各种科学期刊按报导论文数量递减的顺序排列起来,则这些期刊可被分为报导该主题论文数量最大的核心区和含量与核心区相等的几个区。这时,核心区与各后继区所含的期刊数为 1 : n : n 2 . . . 1:n:n^2... 1:n:n2...
RQ3:原始布拉德福定律的局限性
- 布拉德福文献曲线最后的直线部分并非永远是直线,到一定程度时直线部分开始下垂变为曲线,如图2中的虚线所示。
- 分区不应只局限于3个区。原始论文中文字描述是“ 几个区 ”,只是对实例划分为3个区,有些含混不清
参考文献
- 范铮.原始的布拉德福定律[J].图书情报工作,1989,(01):14-17+27.