1、简介
- 梯度表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（梯度的方向）变化最快，变化率（梯度的模）最大，可理解为导数。
- 梯度上升和梯度下降是优化算法中常用的两种方法，主要目的是通过迭代找到目标函数的最大值和最小值。
- 例如：
- 想象我们在一座很高的山上，怎么才能以最快的速度下山？我们可以先选择坡度最倾斜的方向走一段距离，然后再重新选择坡度最倾斜的方向，再走一段距离。以此类推，我们就可以以最快的速度到达山底。（梯度的方向，就是我们要选择的方向）
2、梯度下降
- 梯度下降：梯度下降是一种迭代算法，用于寻找函数的局部最小值或全局最小值。它的核心思想是沿着函数梯度的负方向进行迭代更新，以逐步接近最小值点。在每一次迭代中，根据当前位置的梯度方向来更新参数或变量值，使目标函数值减小。梯度下降算法广泛应用于求解机器学习中的优化问题，如线性回归、逻辑回归、神经网络等。
- 这里我将模拟整个机器学习的流程来解释什么是梯度下降。
2.1、预测函数
- 假设，我们需要建立一个模型用来预测房价。我们拥有一些样本点，现在需要对这些样本点进行拟合。
- 拟合方法：我们可以先随机选一条过原点的直线，然后计算所有样本点和它的偏离程度(误差)，再根据误差大小来调整直线的斜率w。其中，
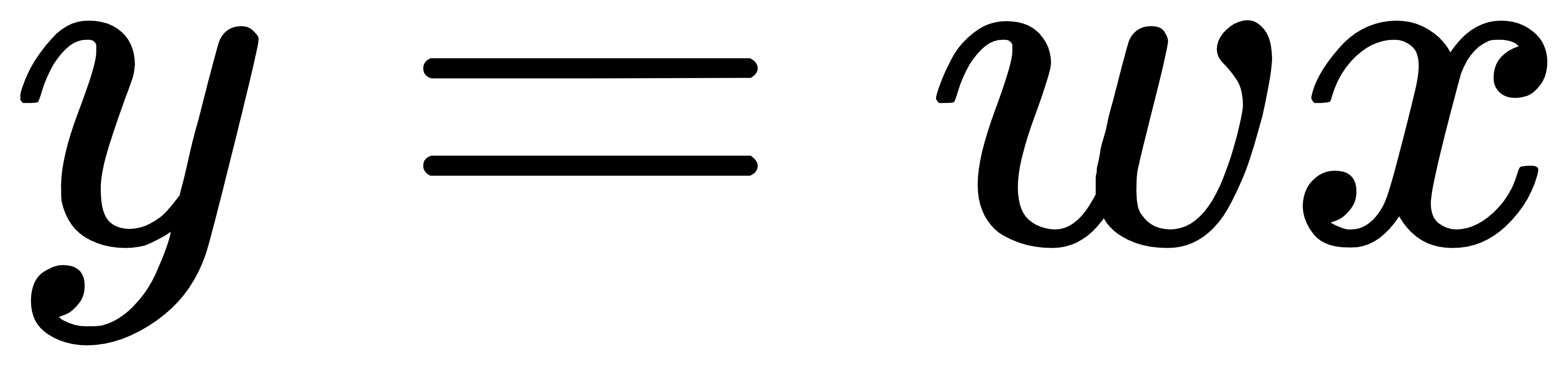为预测函数。 
2.2、代价函数
- 在调整预测函数斜率前，我们需要量化数据的偏离程度，即量化误差。最常见的方法是均方误差，即误差平方和的平均值。
- 假设，样本点p1(x1,y1)对应的误差为e1。
，展开为
- 同理，
- 均方误差为：
，合并同类项得：
- 用字母代替不同项的系数。
- 其中，
即为代价函数。 - 代价函数是用来衡量机器学习模型在给定训练集上的表现的函数，它反映了模型对训练集的拟合程度，可以衡量模型的预测输出与真实输出之间的差异。
- 我们可以看出该代价函数是一个二元函数，图像为抛物线。这样的话，我们就可以把预测函数的拟合过程，转换为代价函数寻找最小值的过程。（代价越小，拟合程度越高）
- 我们要做的就是不断地更新参数w，找到一个w让预测函数值最小。
2.3、计算梯度
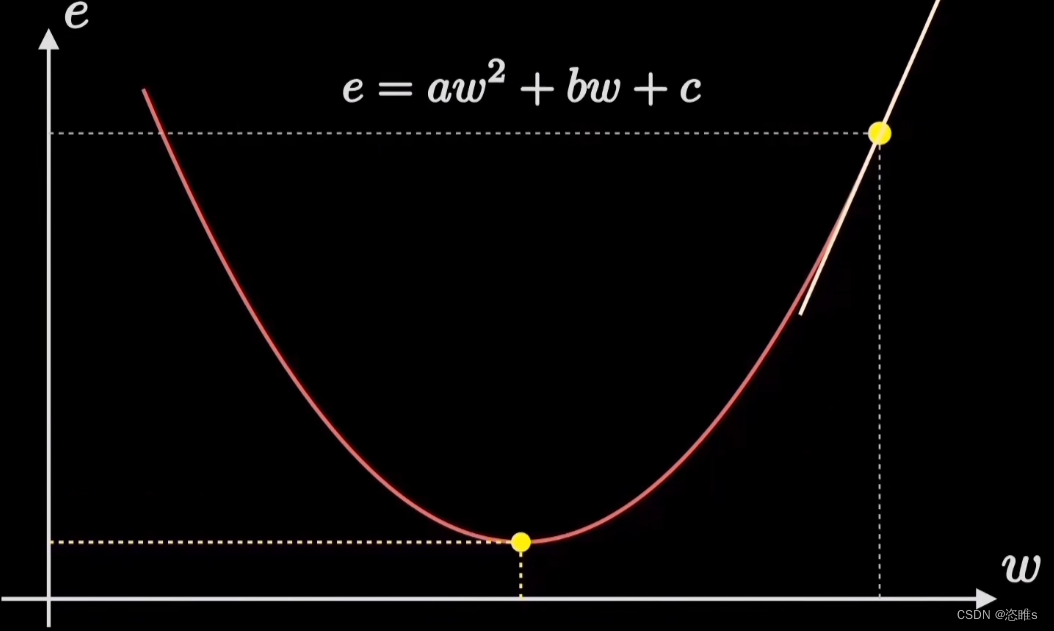
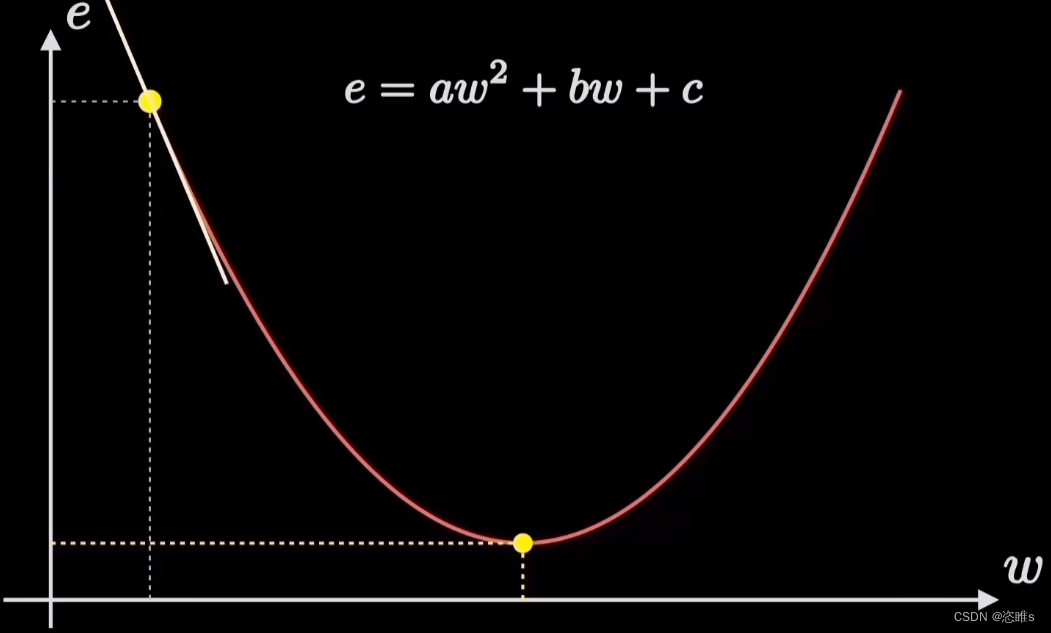
- 机器学习的目标是拟合出最接近训练数据分布的直线，也就是找到使得误差代价最小的参数w，对应在代价函数图像上就是它的最低点。寻找最低点的过程就会使用到梯度下降。
- 假设起始点如图所示，我们只要选择向陡峭程度最大的方向走，就能更快地到达最低点。
- 陡峭程度就是梯度，是代价函数的导数，也是抛物线的曲线斜率。
- 【注】因为这里的代价函数只是二维平面，所以抛物线的斜率即为梯度。而实际应用中，代价函数的图形可能是三维四维的，这时的梯度就是沿着某个方向取得最大值的导数了。
- 所以，计算梯度就是计算代价函数在某个方向取得最大值的导数。
2.4、按学习率前进
- 确定方向以后就需要前进了，这时我们需要确定步长，即更新参数w时的大小和速度。
- 步长太大或太小对梯度下降算法的效果都是不好的。步长太大，函数无法收敛到最小值；步长太小，收敛速度较慢。所以需要找到合适的步长，使其在收敛速度和稳定性之间达到平衡。
- 我们尝试使用斜率（梯度）来作为步长。好处是，斜率较大时，步长稍大些，可以快速收敛；斜率较小时，步长稍小些，收敛的越精准。但在实际过程中，w左右反复横跳，依然无法收敛到最小值，原因是开始时的步长太大。如下图所示。
- 我们让斜率乘以一个非常小的值，即缩小斜率后再当作步长，如0.1，结果就非常顺滑了。这个非常小的值就是学习率。
- 【注】斜率是有正负的，当起始点在最低点左侧时，斜率为负，w逐渐增大；当起始点在最低点右侧时，斜率为正，w逐渐减小。
2.5、循环迭代
- 每次迭代即计算一次梯度，按照梯度的方向前进一段步长。循环迭代就是重复计算梯度和按学习率前进的步骤，直到找到最低点。
3、梯度上升
- 梯度上升：梯度上升是一种迭代算法，用于寻找函数的局部最大值或全局最大值。它的核心思想是沿着函数梯度的正方向进行迭代更新，以逐步接近最大值点。在每一次迭代中，根据当前位置的梯度方向来更新参数或变量值，使目标函数值增大。梯度上升算法适用于求解优化问题中的约束最优化、最大似然估计等。
- 梯度上升和梯度下降类似，只不过方向不同，结合下面公式理解。
