AB试验（二）统计基础

随机变量

• 均值类指标：如用户的平均使用时⻓、平均购买金额、平均购买频率等

• 概率类指标：如用户点击的概率(点击率)、转化的概率(转化率)、购买的概率 (购买率)等

经验结论：在数量足够大时，均值类指标服从正态分布；概率类指标本质上服从二项分布，但当数量足够大时，也服从正态分布。

概率分布

• 正态分布：$X\sim N(\mu ,{\sigma }^2)$
  • 概率密度函数：$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{\mathrm{e}}^{-(x-\mu {)}^2/2{\sigma }^2}$
  • 标准化：$z=\frac{x-\mu }{\sigma }$，$\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$
• 二项分布：$X\sim B(n,p)$
  • 概率质量函数：$P(X=k)=C_n^k{p}^k(1-p{)}^{n-k}$
  • 期望与方差：$E(X)=np$；$D(X)=np(1-p)$

中心极限定理

• 定理：取样样本足够大，则样本均值的分布就趋近于正态分布

• 样本量：约定俗成的，当样本量大于30时就属于足够大

• 案例：通过二项分布近似正态分布

  • 某社交APP在网上投放了广告来吸引用户点击下载。因此一个用户下载情况只存在发生与不发生两种情况，符合二项分布

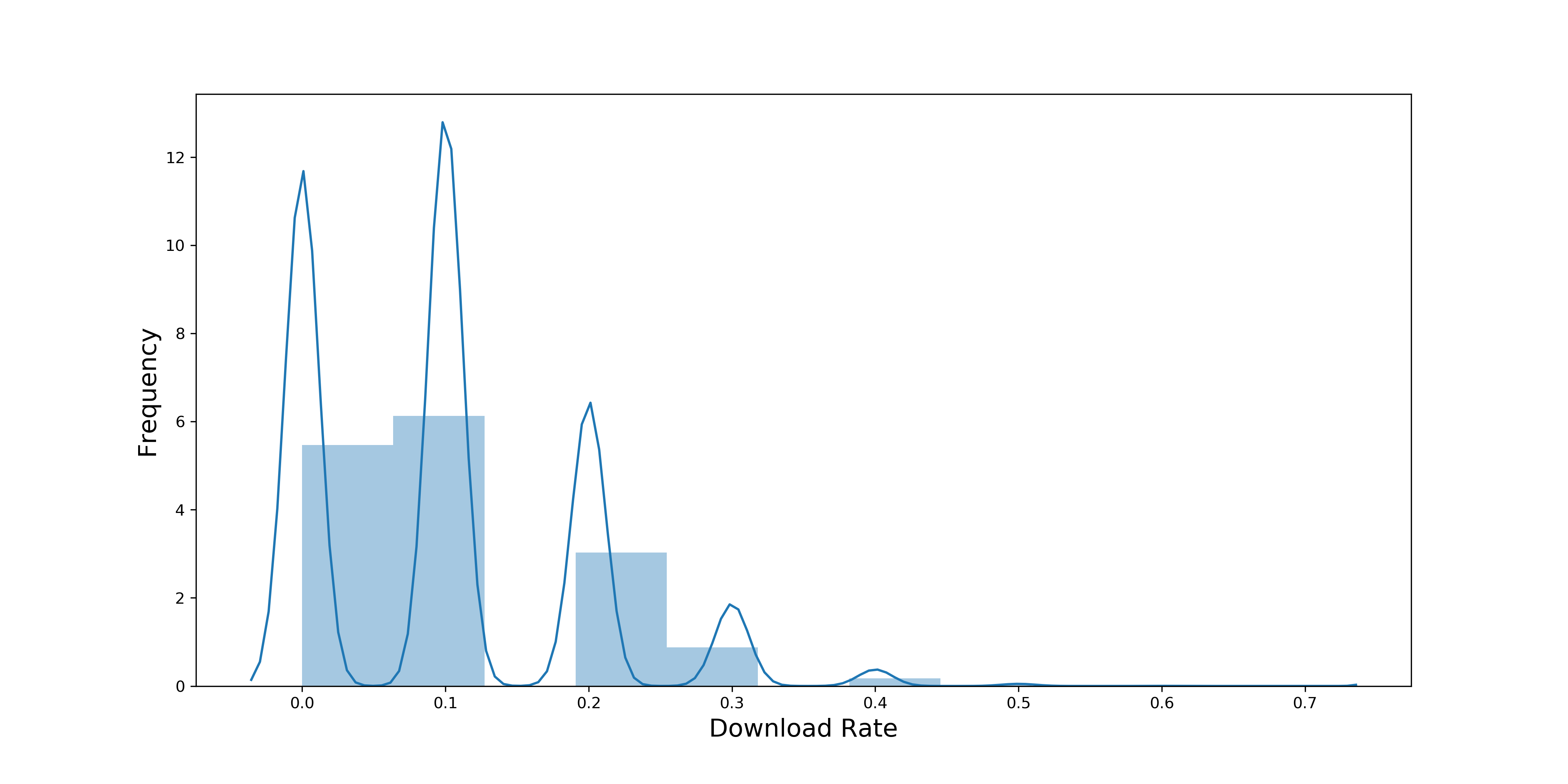
  • 通过一个月的数据观察，发现每分钟平均有10个人会看到广告，平均下载率10%

    

  • 如何理解二项分布中的样本量30

    1. 概率在某种程度上也是平均值，可以把这里的下载率理解为“看到广告的用户的平均下载量”，那我们已经有 43200（602430 ）个数据点了，样本量远远大于 30，但为什么下载率的分布没有像中心极限定理说的那样趋近于正态分布呢?这是因为在二项分布中，中心极限定理说的样本量，指的是计算概率的样本量。在社交 App 的例子中，概率的样本量是 10，因为平均每分钟有 10 人看到广告，还没有达到中心极限定理中说的 30 这个阈值。所以，我们现在要提高这个样本量，才能使下载率的分布趋近正态分布。

    2. 简单的进行样本量提高，可以考虑计算每小时的下载率，因为每小时平均有600人看到广告，样本量也就从10提高到了600。

       

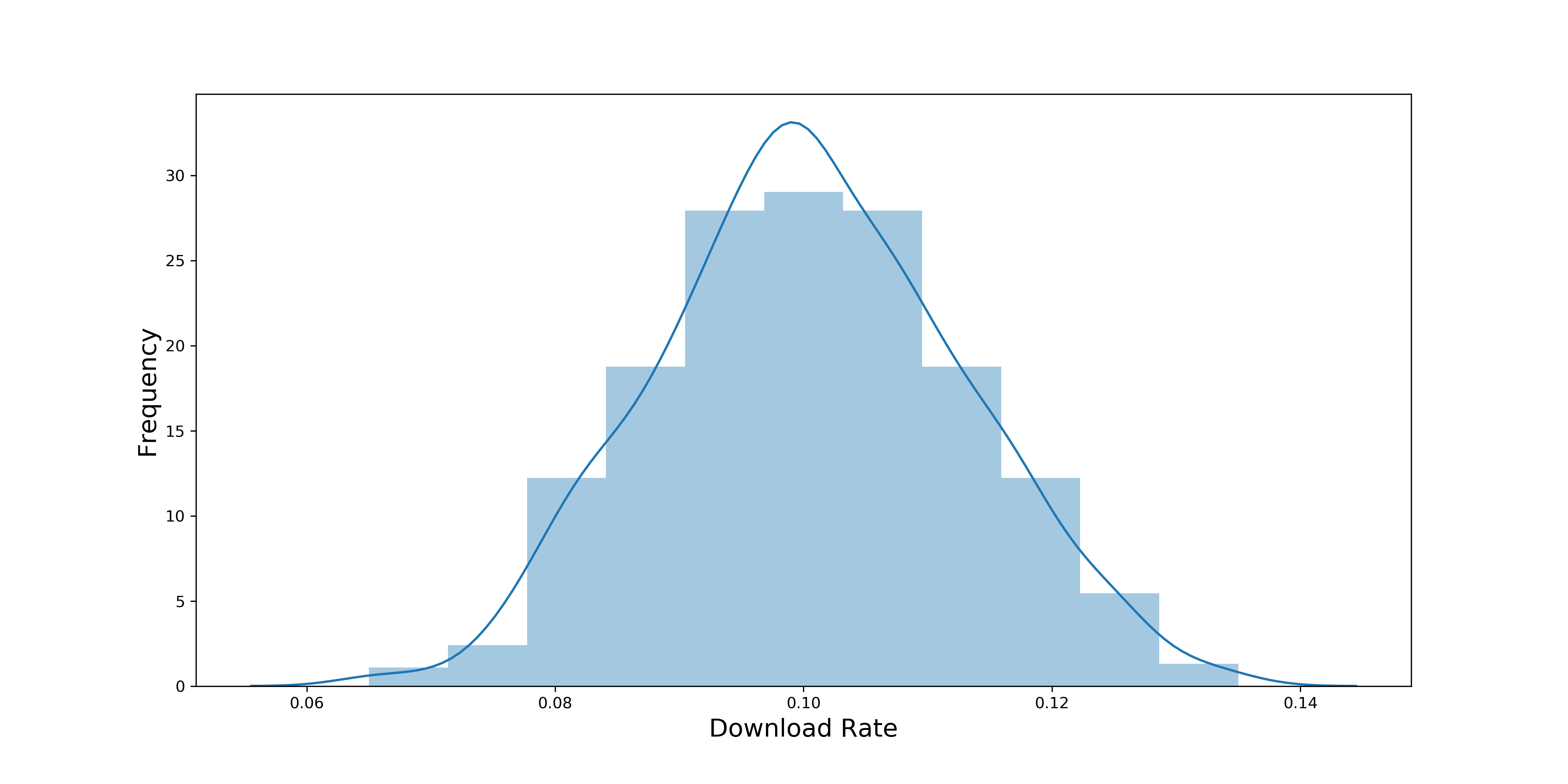
    经验结论：二项分布近似服从正态分布的公式：min(np,n(1-p)) >= 5

    • np或者n(1-p)中相对较小的一方大于等于5，只有二项分布符合这个公式时，才可以近似于正态分布。这是中心极限定理在二项分布中的变体
    • 每分钟下载率：np=10*10%=1，小于5，因此无法近似为正态分布
    • 每小时下载率：np=600*10%=60，大于5，因此可以近似正态分布

假设检验

• 概述：选取一种合适的检验方法，去验证在A/B测试中我们提出的假设是否正确

• 假设：零假设与备则假设

• 检验

  • 从假设角度区分：单尾检验与双尾检验

    经验结论：A/B试验更推荐使用双尾检验

    • 双尾检验可以让数据自身在决策中发挥更大的作用
    • 双尾检验可以帮助我们全面考虑变化带来的正、负面结果

  • 从比较样本的个数区分：单样本检验、双样本检验、配对检验

    经验结论：A/B试验更推荐使用双样本检验

  • 从数据特征区分：t检验、z检验

    经验总结：均值类指标一般用t检验，概率类指标一般用Z检验(比例检验)

    • 样本量大的情况下均值类指标是正态分布，正态分布的总体方差的计算需要知道总体中各个数据的值，这在现实中几乎做不到，因为我们能获取的只是样本数据。所以总体方差不可知，选用t检验
    • 概率类指标是二项分布，二项分布总体方差可以通过样本数据求得总体方差。而且现实中A/B测试的样本量一般都远大于30，所以选用Z检验。这里的比例检验(ProportionTest)是专指用于检验概率类指标的z检验

  经验总结：对于A/B测试来说，要选用双尾，双样本的比例检验(概率类指标)或t检验(均值类指标)

决策

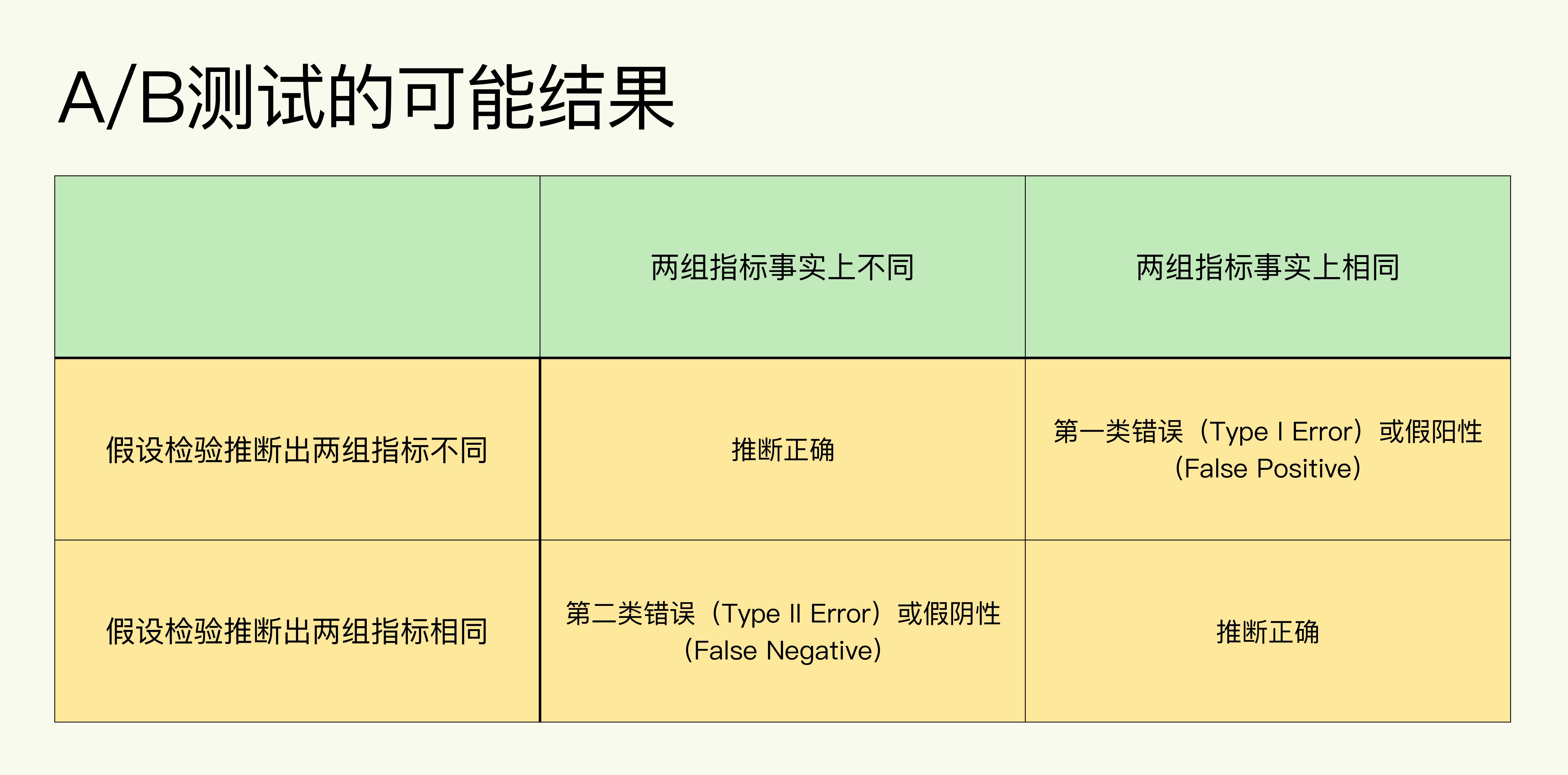
• 两类错误
  • 第一类错误：拒绝了事实上是正确的零假设。发生第一类错误的概率用α表示，也被称为显著水平(Significance Level)。统计上把发生率小于5%的事件称为小概率事件，代表这类事件不容易发生。因此显著水平一般也为5%，而常说的置信水平为1-α。
  • 第二类错误：接受了事实上是错误的零假设。发生第二类错误的概率用β表示，统计上一般定义为20%。而常说的统计功效power=1-β
• 推断
  • p值法：在统计上，p值就是当零假设成立时，我们所观测到的样本数据出现的概率。在A/B测试的语境下，p值就是当对照组和实验组指标事实上是相同时，在A/B测试中用样本数据所观测到的“实验组和对照组指标不同”出现的概率。
    • 如何判断：当P值小于5%时，我们拒绝零假设，接受备择假设，得出两组指标是不同的结论，又叫做结果显著。当P值大于5%时，我们接受零假设，拒绝备择假设，得出两组指标是相同的结论，又叫做结果不显著。
    • 如何计算：比例检验可以用Python的proportions_ztest函数，t检验可以用Python的ttest_ind函数。
  • 置信区间法：在统计上，对于一个随机变量来说，有95%的概率包含总体平均值(Population mean)的范围，就叫做95%的置信区间。可以直接把它理解为随机变量的波动范围，95%的置信区间就是包含了整个波动范围的95%的区间。
    • 如何判断：置信区间是否包括0。如果包括0的话意味着两组指标有可能相同，如果不包括0则说明两组指标不同
    • 如何计算：比例检验可以用Python的confint_proportions_2indep函数，t检验可以用Python的tconfint_diff函数。

总结

日常A/B最常见的就是分析概率类指标和均值类指标，经验上，概率类指标采用双尾双样本比例检验（z），可用proportions_ztest函数计算p值，confint_proportions_2indep函数计算指标差值的置信区间；均值类指标采用双尾双样本t检验，可用ttest_ind函数计算p值，tconfint_diff函数计算指标差值的置信区间。

共勉～