题目

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

• 1 <= target <= 109
• 1 <= nums.length <= 105
• 1 <= nums[i] <= 105

分析

这道题我们使用滑动窗口来解决比较方便，也是双指针的一种用法。
①定义头尾指针，都指向第一个元素，尾指针不断后移，找到第一个符合条件的子数组长度，我们把这个长度叫做窗口；
②因为我们要找的是长度最小的子数组，所以后面要找的子数组长度一定是小于或者等于我们第一个窗口的，将第一个窗口后移
③第一个窗口后移的操作：先是头指针后移，这个时候要计算一下窗口范围内的元素和，看是否满足条件，如果满足题目条件则可以缩小窗口范围，这说明有长度更小的子数组满足我们的要求；如果不满足条件，则尾指针后移，窗口范围不变。

以nums = [2,3,1,2,4,3]为例：

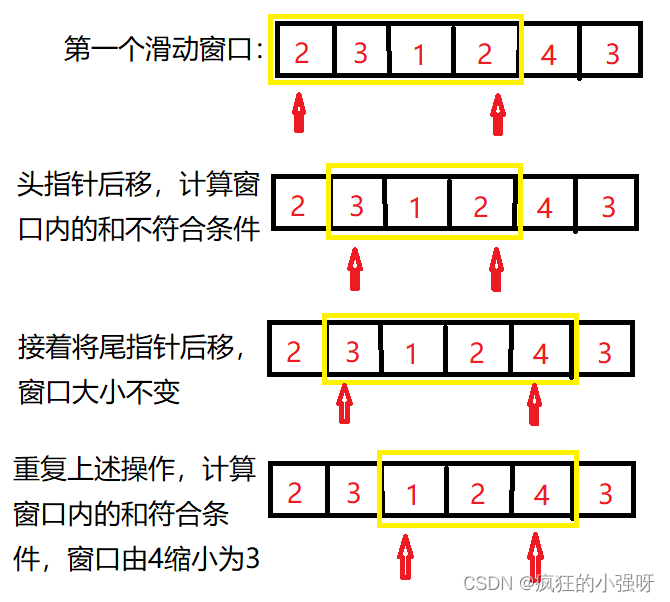
代码（C语言实现）：

int minSubArrayLen(int target, int* nums, int numsSize){
    int sum=0;  //记录子数组（窗口）的和
    int start=0;  //头指针位置
    int len=0;   //子数组（窗口）大小
    int res=1000000;  //最终结果
    for(int end=0;end<numsSize;end++){
        sum=sum+nums[end];   //统计窗口和
       //满足条件
        while(sum>=target){
            len=end-start+1;  //计算窗口大小
            res=len<res?len:res;  //当前长度更小则更新结果
            sum=sum-nums[start++];  //头指针前移一格
        }
        // 否则end++，尾指针前移一格
    }
    return res==1000000?0:res; //如果res=1000000，说明没有符合条件的子数组，返回0
}