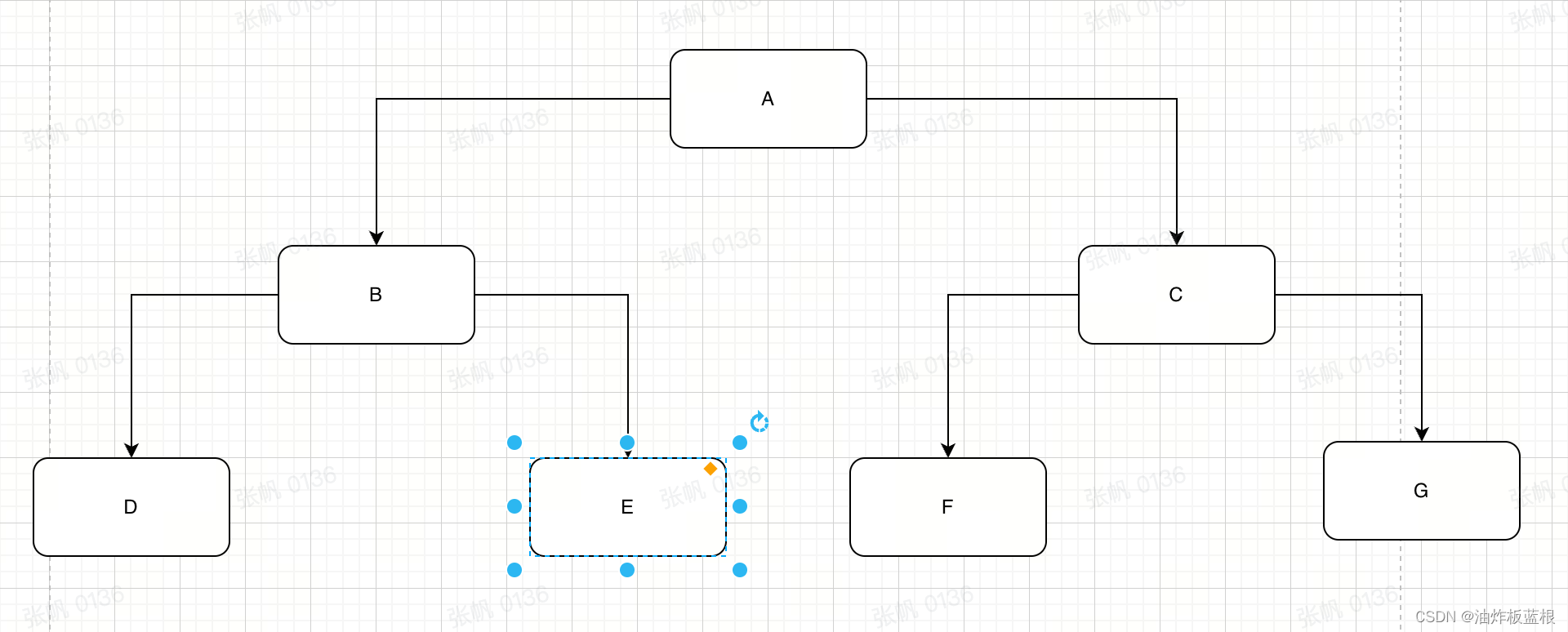
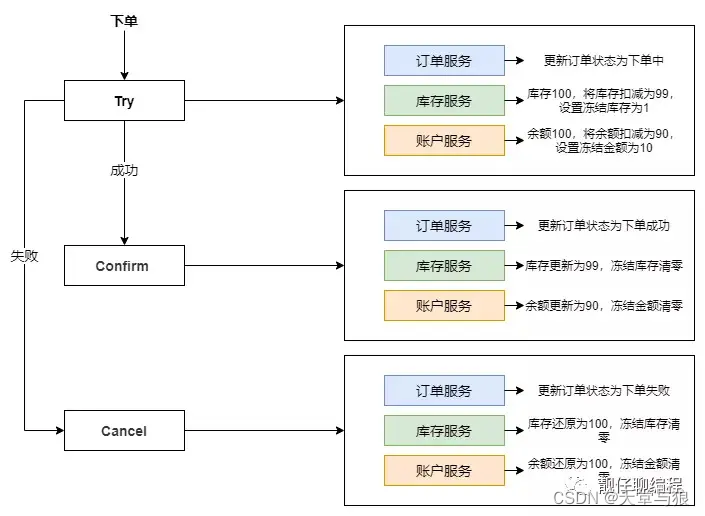
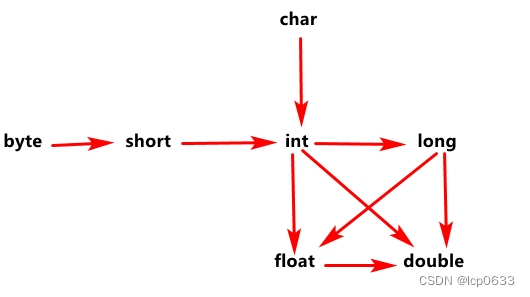
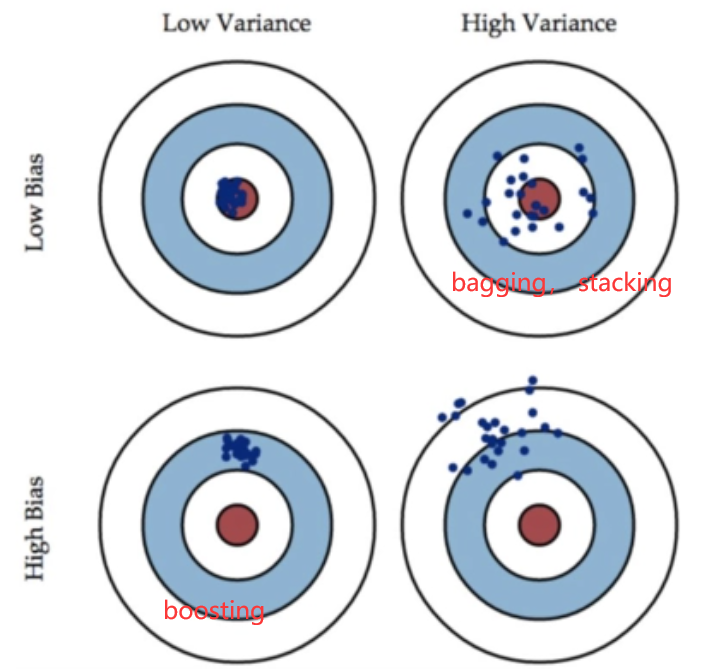
我们如果需要看某段代码的执行耗时，会通过如下的方式进行查看

using System.Diagnostics;

        private void button1_Click(object sender, EventArgs e)
        {
            Stopwatch sw = Stopwatch.StartNew();
            //sw.Start();
            StringBuilder sb = new StringBuilder();
            for(int i = 0; i < 100000; i++)
            {
                sb.Append(i.ToString());
            }

            sw.Stop();
            label1.Text = sw.ElapsedMilliseconds.ToString();
        }

 

特此记录

anlog

2023年8月25日