一、什么是进制

进制是一种用来表示数值的系统或方法，它是基于一个特定的基数来工作的。在我们常见的几种进制中，有：

1. **二进制（基数 2）**：
   二进制只用两个数字：0和1。这是计算机内部使用的数制系统，因为计算机的基本单元（比特）只有两种状态：0或1。

2. **十进制（基数 10）**：
   十进制是我们日常最常用的数制系统，它包括十个数字：0到9。

3. **八进制（基数 8）**：
   八进制使用八个数字：0到7。它在计算机科学中偶尔会被使用，因为它可以更简洁地表示二进制数。

4. **十六进制（基数 16）**：
   十六进制使用十六个符号来表示数值：0到9，然后是A到F（表示10到15）。它也常在计算机科学中用来更简洁地表示二进制数。

在不同进制间转换时，主要是通过不断地除以基数并取余数来完成的。例如，要将一个十进制数转换为二进制，可以将该数除以2，并记录余数，然后再将商除以2，并记录新的余数，如此继续，直到商为0。然后，将所有余数倒序排列，即得到二进制表示。

二、进制在生活中的例子

以下是几种不同进制在生活或科技中的实际应用例子：

1. **二进制（基数 2）**：
   - **计算机系统**: 计算机内部使用二进制来处理和存储数据。所有的程序和文件最终都是以二进制的形式存储。
   - **条形码和QR码**: 通过表示0和1的黑白条纹（或方块），可以编码信息。

2. **十进制（基数 10）**：
   - **日常计数和计算**: 我们在日常生活中进行的大多数计数和计算都是基于十进制的。
   - **货币系统**: 大多数的货币系统也都是基于十进制的，例如美元、欧元等。

3. **八进制（基数 8）**：
   - **早期计算机系统**: 在某些早期计算机系统中，八进制曾被用作一种方便的方式来表示二进制数，因为它可以更紧凑地表示二进制数。
   - **文件权限（Unix/Linux系统）**: 在Unix和Linux系统中，文件权限通常是用八进制数来表示的。

4. **十六进制（基数 16）**：
   - **计算机编程**: 在计算机编程中，十六进制常用于表示内存地址和二进制代码。
   - **颜色代码**: 在HTML和CSS中，颜色通常是用十六进制代码来表示的，例如 `#FFFFFF` 代表白色。

5. **六十进制/六十基数（Sumerians和Babylonians用过）**：
   - **时间单位**: 我们的时间单位（小时、分钟和秒）部分采用了六十进制，例如一小时有60分钟，一分钟有60秒。
   - **地理坐标系统**: 地理坐标系统（度、分、秒）也是基于60的。

6. **十二进制（基数 12）**：
   - **尺寸和长度**: 在某些文化中，十二进制用于计算长度和尺寸（例如一打为12个单位）。
   - **古代货币系统**: 有些古代货币系统是基于12的，例如英国的先前货币系统（先令）。

通过这些例子，我们可以看到不同的进制在我们的日常生活和科技中有广泛的应用。

三、在计算机里的进制

1.二进制

        C语言中，我们如果想表示一个二进制数，可以用0b作为前缀，然后跟上0和1组成的数字，我们来看看一段代码。

C语言：

#include<stdio.h>
int main(){
	int a=0b101;
	printf("%d\n",a);
	return 0;
}

这个是英雄师傅说的但是还是输出不出来二进制，至少再在dev c++是这么回事。 

2.八进制

思考题

一天上课老师问全班同学

C语言：

#include<stdio.h>
int main(){
	int a=0123;
	printf("%d\n",a);
	return 0;
}

小A不假思索的说应该输出123，很快教室里很多同学都同意小a的观点，而坐在后排的小B思考一段时间过后，却说不答案应该是83

请问应该输出应该是什么？

答案：

83，为什么呢因为在C语言中八进制的表示法是前缀1个0，然后跟上0-7的数字，本文中老师并没有说一定是10进制。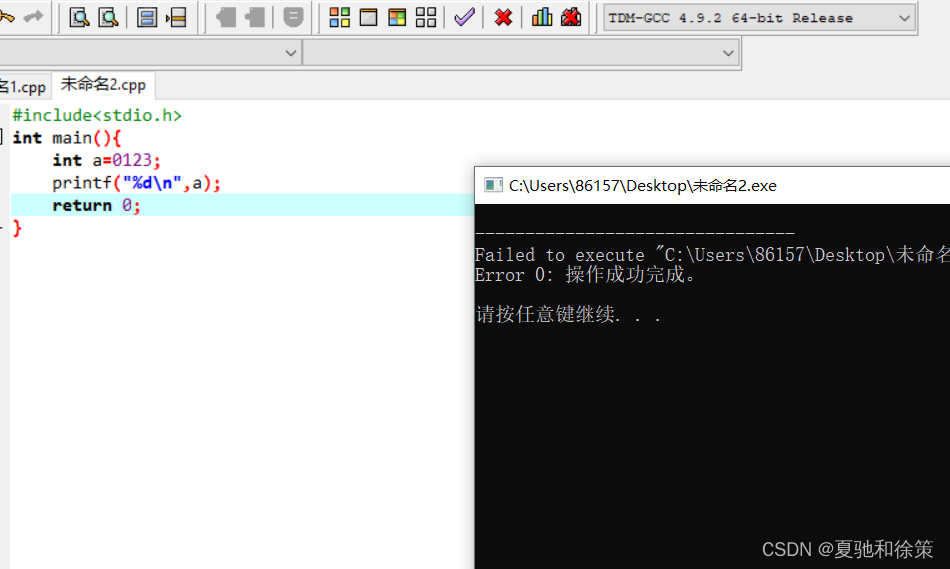

英雄师傅认为，八进制的表示法是前缀1个0然后跟上0-7的数字但是我却输出不出来，这是为什么呢？

我查资料后发现：

• 在C语言中，我们使用了%o格式说明符来输出八进制数，而对于二进制输出，我们需要手动实现一个循环来显示每一位。
• 在C++中，我们可以使用std::oct和std::bitset来分别输出八进制和二进制数。
• 在Java中，我们使用Integer.toOctalString和Integer.toBinaryString方法来输出八进制和二进制数。

       C语言：

#include <stdio.h>

int main() {
    int num = 42;
    
    // 输出八进制数
    printf("Octal: %o\n", num);
    
    // 输出二进制数（C语言标准库不直接支持二进制输出，我们可以自定义一个函数来实现）
    for(int i = 31; i >= 0; i--) {
        printf("%d", (num >> i) & 1);
    }
    printf("\n");
    
    return 0;
}

C++：

#include <iostream>
#include <bitset>

int main() {
    int num = 42;
    
    // 输出八进制数
    std::cout << "Octal: " << std::oct << num << std::dec << std::endl;

    // 输出二进制数
    std::cout << "Binary: " << std::bitset<32>(num) << std::endl;

    return 0;
}

JAVA：

public class Main {
    public static void main(String[] args) {
        int num = 42;
        
        // 输出八进制数
        System.out.println("Octal: " + Integer.toOctalString(num));

        // 输出二进制数
        System.out.println("Binary: " + Integer.toBinaryString(num));
    }
}

3.十六进制

同样看一下代码：

#include<stdio.h>
int main(){
	int a=0x123;
	printf("%d\n",a);
	return 0;
}

输出因该是什么？

输出的应该是291.

四、进制转化初步

### 1. x进制转10进制

任何x进制的数可以使用以下公式转换为十进制数：

\[
\text{{十进制结果}} = \sum \text{{(单个数字)} \times (\text{{基数}})^{\text{{位置}}}}
\]

其中“位置”是从右向左计数，从0开始。

#### 示例

将二进制`1101`转换为十进制：

\[
1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 8 + 4 + 0 + 1 = 13
\]

### 2. 10进制转x进制

将一个十进制数转换为x进制通常可以通过以下步骤完成：

1. 将十进制数除以x，记录余数。
2. 将商继续除以x，再次记录余数。
3. 重复步骤2，直到商为0。
4. 将记录的余数反向排列，得到x进制的表示。

#### 示例

将十进制`13`转换为二进制：

1. \(13 \div 2 = 6\), 余数 = 1
2. \(6 \div 2 = 3\), 余数 = 0
3. \(3 \div 2 = 1\), 余数 = 1
4. \(1 \div 2 = 0\), 余数 = 1

所以二进制表示为：`1101`

这就是如何进行x进制到10进制和10进制到x进制的转换。