文章目录
- 对偶问题实例
- 对偶问题定义和性质
- 定义
- 性质
- 对偶问题应用
- 影子价格
- 理论应用
- 参考文献
对偶问题实例
之前在很多地方,都看到过“对偶”这两个字眼,总觉得这个词很高大上。对偶理论的百度百科中甚至写到:“在线性规划早期发展中最重要的发现是对偶问题”。所以,既然已经到了线性规划这里,那对偶问题自然也值得深入学习一下。
大概了解了一下网上关于对偶问题的介绍,差不多可以分为两类:一类是直接介绍线性规划对偶问题,另一类是从拉格朗日对偶问题开始,然后再表达线性规划作为一种特殊的优化问题,有着特殊的性质。鉴于这段时间都是线性规划方面的内容,个人觉得还是第一类比较适合我。
先举个例子,来直观认识一下对偶问题。
家具公司A生产书桌、餐桌和椅子。每种家具的生产都需要木材和两种熟练劳动:抛光和木工。制作每种家具所需的各种资源的数量、可用资源量以及每种家具的售价如下表所示。
| 资源 | 书桌 | 餐桌 | 椅子 | 可用资源量 |
|---|---|---|---|---|
| 木材(立方米) | 8 | 6 | 1 | 48 |
| 抛光时间(小时) | 4 | 2 | 1.5 | 20 |
| 木工时间(小时) | 2 | 1.5 | 0.5 | 8 |
| 售价(元) | 600 | 300 | 200 |
求该公司应如何安排生产,才能使得收入最大化。
该问题的求解并不困难。设书桌的产量为
x
1
x_1
x1,餐桌的产量为
x
2
x_2
x2,椅子的产量为
x
3
x_3
x3,此时模型可以描述为
m
a
x
f
=
600
x
1
+
300
x
2
+
200
x
3
s.t
8
x
1
+
6
x
2
+
x
3
≤
48
4
x
1
+
2
x
2
+
1.5
x
3
≤
20
2
x
1
+
1.5
x
2
+
0.5
x
3
≤
8
x
1
,
x
2
,
x
3
≥
0
,
且取整数
max \quad f=600x_1+300x_2+200x_3 \\ \text{s.t} \quad 8x_1+6x_2+x_3≤48 \\\nonumber \quad \quad \quad4x_1+2x_2+1.5x_3≤20\\\nonumber \quad\quad\quad 2x_1+1.5x_2+0.5x_3≤8\\\nonumber \quad\quad\quad x_1,x_2,x_3≥0,且取整数\\
maxf=600x1+300x2+200x3s.t8x1+6x2+x3≤484x1+2x2+1.5x3≤202x1+1.5x2+0.5x3≤8x1,x2,x3≥0,且取整数
显然该问题是个整数规划问题,我们使用ortools求解,代码如下
from ortools.linear_solver import pywraplp
if __name__ == '__main__':
# 声明ortools求解器,使用SCIP算法
solver = pywraplp.Solver.CreateSolver('SCIP')
# 优化变量,连续值
x1 = solver.NumVar(0, solver.infinity(), 'x1')
x2 = solver.NumVar(0, solver.infinity(), 'x2')
x3 = solver.NumVar(0, solver.infinity(), 'x3')
# 目标函数
solver.Maximize(600 * x1 + 300 * x2 + 200 * x3)
# 约束条件
solver.Add(8 * x1 + 6 * x2 + x3 <= 48)
solver.Add(4 * x1 + 2 * x2 + 1.5 * x3 <= 20)
solver.Add(2 * x1 + 1.5 * x2 + 0.5 * x3 <= 8)
# 模型求解
status = solver.Solve()
# 模型求解成功, 打印结果
if status == pywraplp.Solver.OPTIMAL:
# 变量最优解
print('x1: {}, x2: {}, x3: {}'.format(x1.solution_value(), x2.solution_value(), x3.solution_value()))
# 最优目标函数值
print('best_f =', solver.Objective().Value())
else:
print('not converge.')
运行代码后,可以得到最优解如下
x1: 1.9999999999999996, x2: 0.0, x3: 8.0
best_f = 2800.0
需要注意的是,问题本身是个整数规划,但代码中并未限制变量只能取整数。不过由于该线性规划问题的最优解也是整数,所以结果并不影响。这么做,主要是为了方便后续和对偶问题做对比。
那对偶问题是什么呢?对偶问题可以理解从另一个角度提出问题。
新问题的描述如下:假定公司B想购买A公司的所有资源,此时便需要确定每种资源的单价。设定购买木材的单价是 w 1 w_1 w1(元/立方米),抛光时间的单价是 w 2 w_2 w2(元/小时),木工时间的单价是 w 3 w_3 w3(元/小时)。
一方面,B自然是期望总价格越低越好,所以目标函数为
m
i
n
z
=
48
w
1
+
20
w
2
+
8
w
3
min \quad z=48w_1+20w_2+8w_3
minz=48w1+20w2+8w3
另一方面,A愿意售卖自己资源的条件是:售卖的价格不能低于用同等数量资源由自己组织生产时取得的盈利。针对书桌来说,B至少需要支付600元,才能买得8立方米木材、4小时的抛光时间和2小时的木工时间。该约束条件可以描述为
8
w
1
+
4
w
2
+
2
w
3
≥
600
8w_1+4w_2+2w_3≥600
8w1+4w2+2w3≥600
通过类似的推理,还可以得到另外两个约束
6
w
1
+
2
w
2
+
1.5
w
3
≥
300
,
w
1
+
1.5
w
2
+
0.5
w
3
≥
200
6w_1+2w_2+1.5w_3≥300, \quad w_1+1.5w_2+0.5w_3≥200
6w1+2w2+1.5w3≥300,w1+1.5w2+0.5w3≥200
显然,单价都不能为负数,所以其约束是
w
1
,
w
2
,
w
3
≥
0
w_1,w_2,w_3≥0
w1,w2,w3≥0
综上,就得到了如下的一个新的线性规划问题
m
i
n
z
=
48
w
1
+
20
w
2
+
8
w
3
s.t
8
w
1
+
4
w
2
+
2
w
3
≥
600
6
w
1
+
2
w
2
+
1.5
w
3
≥
300
w
1
+
1.5
w
2
+
0.5
w
3
≥
200
w
1
,
w
2
,
w
3
≥
0
min \quad z=48w_1+20w_2+8w_3 \\ \text{s.t} \quad 8w_1+4w_2+2w_3≥600 \\\nonumber \quad \quad \quad 6w_1+2w_2+1.5w_3≥300\\\nonumber \quad \quad \quad w_1+1.5w_2+0.5w_3≥200\\\nonumber w_1,w_2,w_3≥0\\
minz=48w1+20w2+8w3s.t8w1+4w2+2w3≥6006w1+2w2+1.5w3≥300w1+1.5w2+0.5w3≥200w1,w2,w3≥0
以上这个线性规划问题就是原问题的对偶问题。
求解一下对偶问题,代码如下
from ortools.linear_solver import pywraplp
if __name__ == '__main__':
# 声明ortools求解器,使用SCIP算法
solver = pywraplp.Solver.CreateSolver('SCIP')
# 优化变量,连续值
x1 = solver.NumVar(0, solver.infinity(), 'x1')
x2 = solver.NumVar(0, solver.infinity(), 'x2')
x3 = solver.NumVar(0, solver.infinity(), 'x3')
# 目标函数
solver.Minimize(48 * x1 + 20 * x2 + 8 * x3)
# 约束条件
solver.Add(8 * x1 + 4 * x2 + 2 * x3 >= 600)
solver.Add(6 * x1 + 2 * x2 + 1.5 * x3 >= 300)
solver.Add(1 * x1 + 1.5 * x2 + 0.5 * x3 >= 200)
# 模型求解
status = solver.Solve()
# 模型求解成功, 打印结果
if status == pywraplp.Solver.OPTIMAL:
# 变量最优解
print('x1: {}, x2: {}, x3: {}'.format(x1.solution_value(), x2.solution_value(), x3.solution_value()))
# 最优目标函数值
print('best_f =', solver.Objective().Value())
else:
print('not converge.')
运行代码,可以得到最优解如下
x1: 0.0, x2: 100.00000000000003, x3: 99.99999999999993
best_f = 2799.9999999999995
对比一下原问题和对偶问题的最优解,我们发现一个有趣的现象
f
∗
=
z
∗
f^{\ast}=z^{\ast}
f∗=z∗
即,原问题和对偶问题的最优目标函数值相等。事实上,这并不是特例,只是线性规划对偶问题的性质之一。
对偶问题定义和性质
定义
上一章的实例让我们对对偶问题有了一些直观的认知,本节通过一些偏理论的推导,来研究清楚线性规划中对偶问题和原问题之间具有怎样的关系和性质。
回顾一下线性规划的标准型
m
i
n
f
(
x
)
=
c
T
x
s.t
A
x
=
b
x
≥
0
min \quad f(\pmb x)=\pmb c^T\pmb x \\ \text{s.t} \quad \pmb A\pmb x=\pmb b \\\nonumber \quad \quad \pmb x ≥ 0\\
minf(x)=cTxs.tAx=bx≥0
在推导单纯形法时,有如下的公式
f
=
c
B
T
B
−
1
b
−
(
c
B
T
B
−
1
N
−
c
N
T
)
x
N
f=\pmb c_B^T\pmb B^{-1}\pmb b-(\pmb c_B^T\pmb B^{-1}\pmb N-\pmb c_N^T)\pmb x_N
f=cBTB−1b−(cBTB−1N−cNT)xN
定义
R
=
c
B
T
B
−
1
N
−
c
N
T
\pmb R=\pmb c_B^T\pmb B^{-1}\pmb N-\pmb c_N^T
R=cBTB−1N−cNT
如果线性规划已经达到最优解,则
R
≤
0
\pmb R≤\pmb 0
R≤0。此时,令
w
T
=
c
B
T
B
−
1
\pmb w^T = \pmb c_B^T\pmb B^{-1}
wT=cBTB−1,上式可以写为
w
T
N
≤
c
N
T
w^T\pmb N≤\pmb c_N^T
wTN≤cNT
再看一下
w
T
B
\pmb w^T\pmb B
wTB项
w
T
B
=
c
B
T
B
−
1
B
=
c
B
T
\pmb w^T\pmb B=\pmb c_B^T\pmb B^{-1} \pmb B=\pmb c_B^T
wTB=cBTB−1B=cBT
因为
A
=
[
B
,
N
]
\pmb A=[\pmb B,\pmb N]
A=[B,N],结合上述两式,可以得到
w
T
A
≤
c
T
\pmb w^T\pmb A≤\pmb c^T
wTA≤cT
加个转置,得到
A
T
w
≤
c
A^T \pmb w ≤ \pmb c
ATw≤c
再看另一组推导
w
T
b
=
w
T
A
x
≤
c
T
x
\pmb w^T \pmb b=\pmb w^T \pmb A \pmb x≤\pmb c^T\pmb x
wTb=wTAx≤cTx
基于上面两个公式,如果我们把
w
\pmb w
w作为变量,可以构建出一个新的优化问题
m
a
x
b
T
w
s.t
A
T
w
≤
c
max \quad \pmb b^T\pmb w \\ \text{s.t} \quad \pmb A^T\pmb w≤\pmb c
maxbTws.tATw≤c
该优化问题就是原线性规划问题的对偶问题。对照原问题看, A , b \pmb A,\pmb b A,b和 c \pmb c c都还在,只是换了位置;同时 x ≥ 0 \pmb x≥0 x≥0但是 w \pmb w w没有约束。
性质
对偶问题既然可以从原问题推导而来,他们之间自然也存在一些相互关系。
个人看来,最基本的关系应该就是弱对偶定理了:若 x \pmb x x是原问题的可行解, w \pmb w w是对偶问题的可行解,则有 c T x ≥ b T w \pmb c^T\pmb x ≥ \pmb b^T \pmb w cTx≥bTw。
该定理从刚刚的推演中,其实已经证明了,这里通过如下的过程再描述一遍
c
T
x
=
x
T
c
≥
x
T
A
T
w
=
b
T
w
\pmb c^T\pmb x = \pmb x^T\pmb c ≥ \pmb x^T\pmb A^T\pmb w=\pmb b^T \pmb w
cTx=xTc≥xTATw=bTw
基于弱对偶定理可以得到一个推论:若 x ∗ \pmb x^\ast x∗是原问题的可行解, w ∗ \pmb w^\ast w∗是对偶问题的可行解,且有 c T x ∗ = b T w ∗ \pmb c^T\pmb x^\ast=\pmb b^T\pmb w^\ast cTx∗=bTw∗,则 x ∗ \pmb x^\ast x∗是原问题的最优解, w ∗ \pmb w^\ast w∗是对偶问题的最优解。
由弱对偶定理可知
c
T
x
≥
b
T
w
∗
\pmb c^T\pmb x≥\pmb b^T\pmb w^\ast
cTx≥bTw∗
同时
c
T
x
∗
=
b
T
w
∗
\pmb c^T\pmb x^\ast=\pmb b^T\pmb w^\ast
cTx∗=bTw∗
所以
x
∗
\pmb x^\ast
x∗是原问题的最优解。
同样的方法,可以证明, w ∗ \pmb w^\ast w∗是对偶问题的最优解。
最后是实际应用中最重要的强对偶定理:若原问题有最优解,则对偶问题也有最优解,且目标函数值相等。
假设原问题最优解为
x
∗
\pmb x^\ast
x∗,对偶变量
w
T
=
c
B
T
B
−
1
\pmb w^T = \pmb c_B^T\pmb B^{-1}
wT=cBTB−1。因为
x
∗
\pmb x^\ast
x∗是最优解,所以
R
=
A
T
w
−
c
≤
0
\pmb R=\pmb A^T\pmb w-\pmb c≤0
R=ATw−c≤0
所以
w
\pmb w
w是对偶问题的可行解。同时
x
\pmb x
x是一个基本可行解,可做如下推演
c
T
x
=
c
B
T
x
B
=
c
B
T
B
−
1
b
=
w
T
b
=
b
T
w
\pmb c^T\pmb x=\pmb c_B^T\pmb x_B=\pmb c_B^T\pmb B^{-1}\pmb b=\pmb w^T\pmb b=\pmb b^T\pmb w
cTx=cBTxB=cBTB−1b=wTb=bTw
结合之前的推论可知,
w
\pmb w
w是对偶问题的最优解。
对偶问题应用
对偶问题的应用是非常多的,不过大部分都是用于理论推导和证明的,在实际应用中比较常见的是影子价格。
影子价格
根据强对偶定理,原问题和对偶问题同时有最优解时,两者的目标函数值相等,即
f
=
c
T
x
∗
=
z
=
b
T
w
∗
f=\pmb c^T\pmb x^\ast=z=\pmb b^T\pmb w^\ast
f=cTx∗=z=bTw∗
写成分量的形式
f
=
w
1
∗
b
1
+
w
2
∗
b
2
+
⋅
⋅
⋅
+
w
m
∗
b
m
f=w_1^\ast b_1+w_2^\ast b_2+···+w_m^\ast b_m
f=w1∗b1+w2∗b2+⋅⋅⋅+wm∗bm
对
b
i
b_i
bi求导
∂
f
∂
b
i
=
w
i
∗
,
i
=
1
,
2
,
⋅
⋅
⋅
,
m
\frac{\partial f}{\partial b_i}=w_i^\ast, \quad i=1,2,···,m
∂bi∂f=wi∗,i=1,2,⋅⋅⋅,m
右边显然就是我们求解对偶问题时得到的最优解;而左边可以直观理解为目标函数值相对于资源变量的梯度值,该值越小,表明相应资源增加后能够带来的目标函数值的降低幅度越大。
接下来举个实例直观说明一下影子价格的含义。
原问题:
m
i
n
f
(
x
)
=
−
5
x
1
−
4
x
2
s.t
x
1
+
3
x
2
+
x
3
=
90
2
x
1
+
x
2
+
x
4
=
80
x
1
+
x
2
+
x
5
=
45
x
1
,
x
2
,
x
3
,
x
4
,
x
5
≥
0
min \quad f(\pmb x)= -5x_1-4x_2 \\ \text{s.t} \quad x_1+3x_2+x_3=90 \\ \nonumber \quad \quad 2x_1+x_2+x_4=80 \\ \nonumber \quad \quad x_1+x_2+x_5=45 \\ \nonumber \quad \quad \quad x_1,x_2,x_3,x_4,x_5≥0
minf(x)=−5x1−4x2s.tx1+3x2+x3=902x1+x2+x4=80x1+x2+x5=45x1,x2,x3,x4,x5≥0
调用ortools求解
from ortools.linear_solver import pywraplp
if __name__ == '__main__':
# 声明ortools求解器,使用SCIP算法
solver = pywraplp.Solver.CreateSolver('SCIP')
# 优化变量
x1 = solver.NumVar(0, solver.infinity(), 'x1')
x2 = solver.NumVar(0, solver.infinity(), 'x2')
x3 = solver.NumVar(0, solver.infinity(), 'x3')
x4 = solver.NumVar(0, solver.infinity(), 'x4')
x5 = solver.NumVar(0, solver.infinity(), 'x5')
# 目标函数
solver.Minimize(-5 * x1 - 4 * x2)
# 约束条件
solver.Add(1 * x1 + 3 * x2 + x3 == 90)
solver.Add(2 * x1 + 1 * x2 + x4 == 80)
solver.Add(1 * x1 + 1 * x2 + x5 == 45)
# 模型求解
status = solver.Solve()
# 模型求解成功, 打印结果
if status == pywraplp.Solver.OPTIMAL:
# 变量最优解
print('x1: {}, x2: {}, x3: {}, x4: {}, x5: {}'.format(
x1.solution_value(), x2.solution_value(), x3.solution_value(),
x4.solution_value(), x5.solution_value()))
# 最优目标函数值
print('best_f =', solver.Objective().Value())
else:
print('not converge.')
运行代码后,得到最优解为
x1: 35.0, x2: 10.000000000000007, x3: 24.99999999999998, x4: -7.105427357601002e-15, x5: -7.105427357601002e-15
best_f = -215.00000000000003
对偶问题:
m
a
x
z
(
w
)
=
90
w
1
+
80
w
2
+
45
w
3
s.t
w
1
+
2
w
2
+
w
3
≤
−
5
3
w
1
+
w
2
+
w
e
3
≤
−
4
w
1
,
w
2
,
w
3
≤
0
max \quad z(\pmb w)= 90w_1+80w_2+45w_3 \\ \text{s.t} \quad w_1+2w_2+w_3≤-5 \\ \nonumber \quad \quad 3w_1+w_2+w_e3≤-4 \\ \nonumber w_1,w_2,w_3≤0
maxz(w)=90w1+80w2+45w3s.tw1+2w2+w3≤−53w1+w2+we3≤−4w1,w2,w3≤0
还是调用ortools求解
from ortools.linear_solver import pywraplp
if __name__ == '__main__':
# 声明ortools求解器,使用SCIP算法
solver = pywraplp.Solver.CreateSolver('SCIP')
# 优化变量
x1 = solver.NumVar(-solver.infinity(), solver.infinity(), 'x1')
x2 = solver.NumVar(-solver.infinity(), solver.infinity(), 'x2')
x3 = solver.NumVar(-solver.infinity(), solver.infinity(), 'x3')
# 目标函数
solver.Maximize(90 * x1 + 80 * x2 + 45 * x3)
# 约束条件
solver.Add(1 * x1 + 2 * x2 + x3 <= -5)
solver.Add(3 * x1 + 1 * x2 + x3 <= -4)
solver.Add(1 * x1 <= 0)
solver.Add(1 * x2 <= 0)
solver.Add(1 * x3 <= 0)
# 模型求解
status = solver.Solve()
# 模型求解成功, 打印结果
if status == pywraplp.Solver.OPTIMAL:
# 变量最优解
print('x1: {}, x2: {}, x3: {} '.format(x1.solution_value(), x2.solution_value(), x3.solution_value()))
# 最优目标函数值
print('best_f =', solver.Objective().Value())
else:
print('not converge.')
运行代码后,得到最优解为
x1: 0.0, x2: -1.0000000000000002, x3: -3.0
best_f = -215.00000000000006
显然,最优目标函数值是相同的。
如果修改原问题代码中的第一个约束条件:90->91,即第一个资源变量增加1个单位,重新计算得到最优解为
x1: 35.0, x2: 10.000000000000005, x3: 25.999999999999986, x4: -5.329070518200751e-15, x5: -5.329070518200751e-15
best_f = -215.0
此时最优目标函数值没变;从对偶问题的最优解可知, w 1 ∗ = 0 w_1^\ast=0 w1∗=0,是符合逻辑的。
如果修改原问题代码中的第二个约束条件:80->81,重新计算得到最优解为
x1: 36.0, x2: 9.000000000000004, x3: 26.99999999999999, x4: -3.552713678800501e-15, x5: -3.552713678800501e-15
best_f = -216.00000000000003
此时最优目标函数值降低了1个单位;从对偶问题的最优解可知, w 2 ∗ = − 1 w_2^\ast=-1 w2∗=−1,也是符合逻辑的。
如果修改原问题代码中的第三个约束条件:45->46,重新计算得到最优解为
x1: 34.00000000000001, x2: 11.999999999999995, x3: 20.000000000000007, x4: -8.881784197001252e-15, x5: -1.7763568394002505e-15
best_f = -218.00000000000003
此时最优目标函数值降低了3个单位;从对偶问题的最优解可知, w 3 ∗ = − 3 w_3^\ast=-3 w3∗=−3,所以依然没问题。
最近恰好遇到了一篇工业场景中尝试使用影子价格的案例:Inventory Based Recommendation Algorithms
,就简单说一下自己的理解。
先描述一下场景:盒马鲜生的购物车界面处,可以推荐一些易逝品,这些商品当天不卖完,第二天就要报废或做折价处理。每个商品的库存数量是有限的。最理想的状态,应该是当天所有商品都能卖完。那每个用户进入购物车页面时,系统应该推荐哪些商品呢?
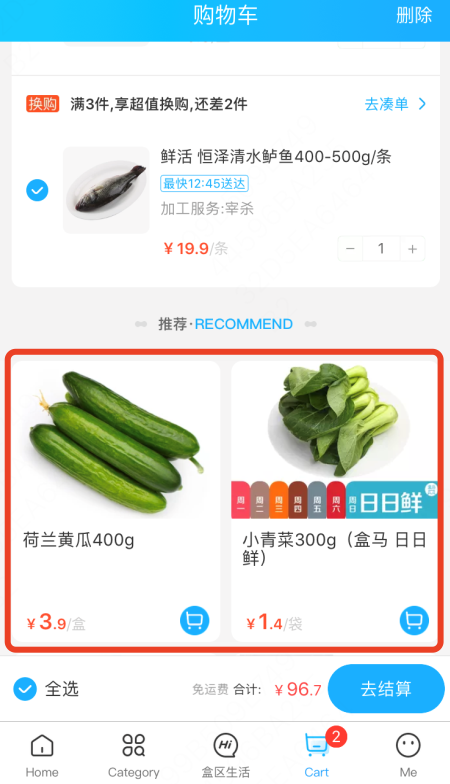
最容易想到的策略是:计算每件商品被推荐时能带来的价值
c
t
r
i
∗
c
v
r
i
∗
r
i
ctr_i*cvr_i*r_i
ctri∗cvri∗ri
其中,
c
t
r
i
ctr_i
ctri、
c
v
r
i
cvr_i
cvri和
r
i
r_i
ri分别为第
i
i
i件商品的点击率、转化率和价格。
有了该值后,将商品按照此值从大到小排列并推荐top K即可。
这个策略的一个潜在问题是未考虑商品的库存,可能会导致一些高价值的商品早早售罄,而中等价值的商品却因为推荐次数过少等原因没有卖完。
为了解决该问题,便可以引入影子价格对上述策略进行微调:
c
t
r
i
∗
c
v
r
i
∗
(
r
i
−
α
i
)
ctr_i*cvr_i*(r_i-\alpha_i)
ctri∗cvri∗(ri−αi)
其中,
α
i
\alpha_i
αi即为第
i
i
i个商品的库存约束对应的影子价格。
加了影子价格参数后,当高价值商品的库存充足时,商品的影子价格为0,不影响原推荐策略;当高价值商品的库存变少后,商品变得稀缺,影子价格便会大于0,从而降低高价值商品的排序,从而让位于其他价值稍低但库存较多的商品。
理论应用
偏理论一些的应用,这里也简单提一下:
(1) 首先是为求解线性规划问题提供了一个新的方法:对偶单纯形法;
(2) 其次是为证明原问题无解提供一个新的思路:Farkas引理;
(3) 最后一个有些扩展:无论原问题是否为凸问题,其拉格朗日对偶问题一定是凸优化问题。
参考文献
此前文章中都没有这一章节,但在实际学习和总结的过程中,其实已经参考了很多大神的文章或视频,而这些参考很难在某句话中添加引用或者链接以表达对原作者成果的致敬,因为很多新认知被散落在了文章的各个角落。所以为了方便,以后统一放在这个位置。
对偶问题实例:https://weread.qq.com/web/reader/da232bb072012022da29f24kc7432af0210c74d97b01b1c
为何需要线性规划的的对偶问题:https://www.zhihu.com/question/26658861
对偶问题推导:https://zhuanlan.zhihu.com/p/522590887
拉格朗日对偶:https://blog.csdn.net/frostime/article/details/90291392?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1
影子价格在盒马中的应用:https://ieeexplore.ieee.org/abstract/document/9378261