目录
一、定义
深度优先遍历通常用于解决以下问题:
深度优先遍历算法具有以下优点:
深度优先遍历算法的一个缺点是:
二、代码
空间复杂度:
时间复杂度:
邻接矩阵存储:
邻接表存储:
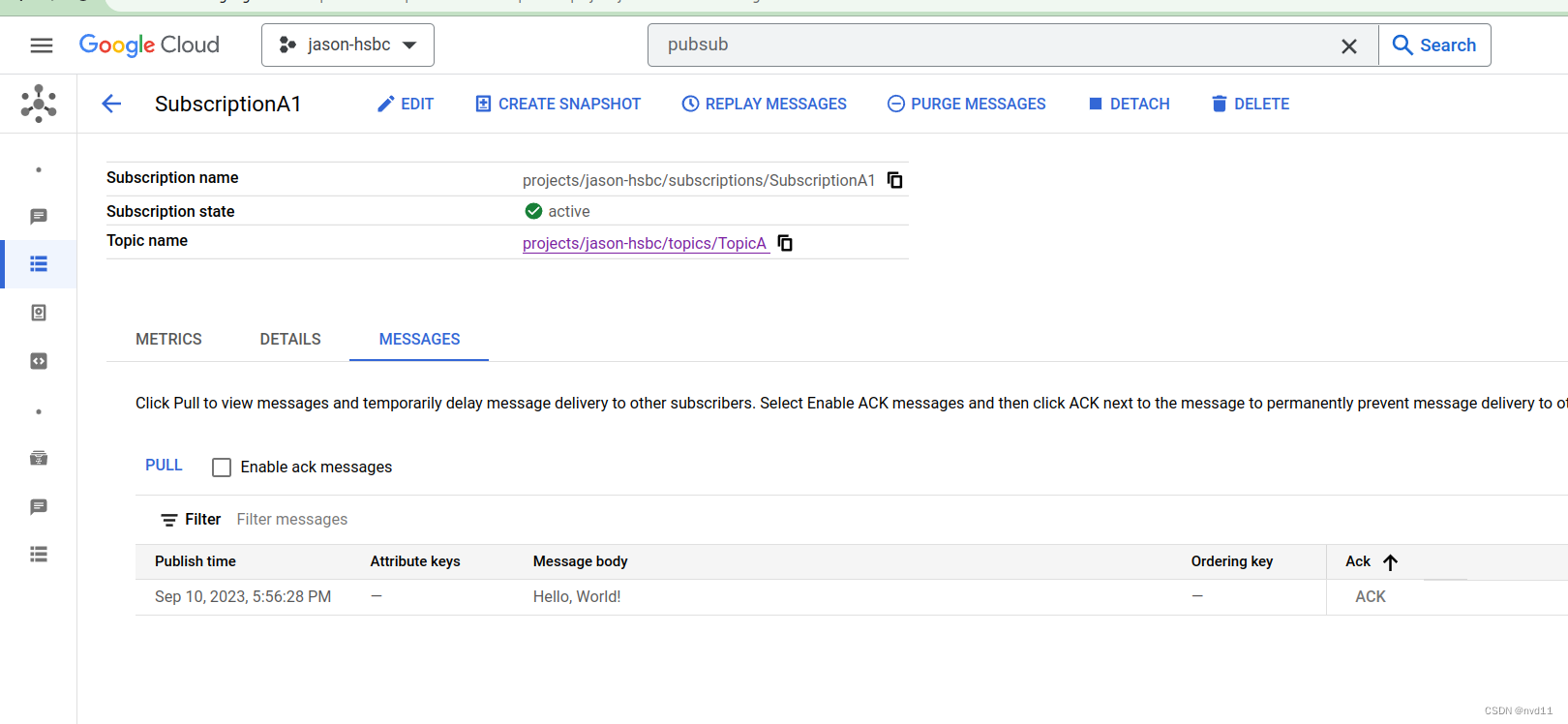
三、手动模拟深度优先遍历⭐⭐⭐⭐⭐
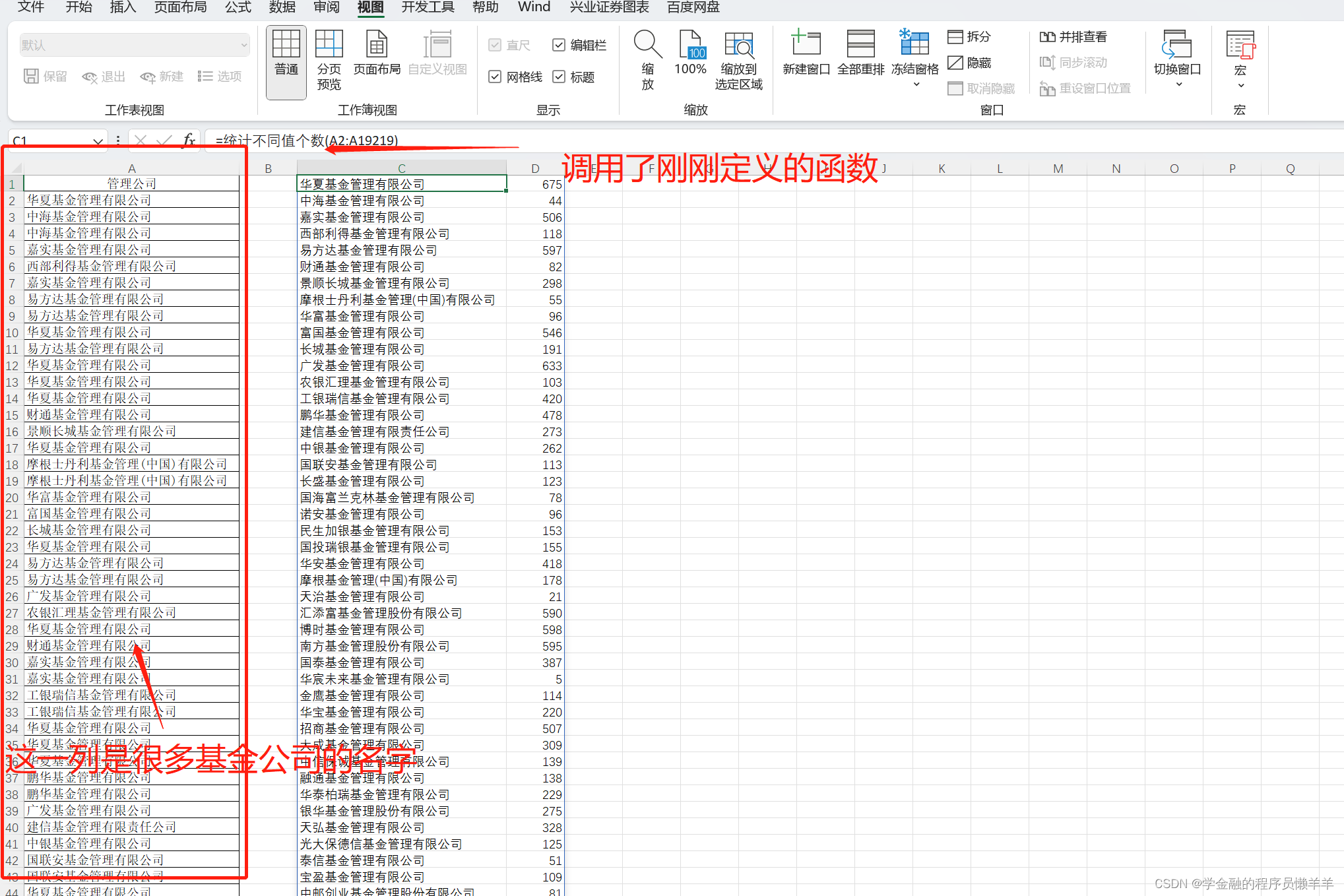
1、首先访问结点2
2、访问2的邻接点6
3、跳转到6,访问6的邻接结点,发现2已经被访问过了,于是访问7
4、跳转到7,访问7的邻接结点,6被访问过了所以跳过,访问8
5、跳转到8,访问8的邻接结点,访问4
6、继续访问跳转到4,访问4的邻接结点,访问3
7、跳转到3,访问3的邻接结点,访问6,6被访问过了(跳过),访问7(跳过),访问4(跳过),由于3的邻接结点都被访问完了,所以返回上一级;
8、遍历4,访问8(跳过),访问7(跳过),返回上一级;
9、上一级是8,所以遍历8,访问7(跳过),返回上一级;
10、遍历7,访问3(跳过),访问4(跳过),返回上一级;
11、遍历6,访问3(跳过),返回上一级;
12、遍历2,访问1;
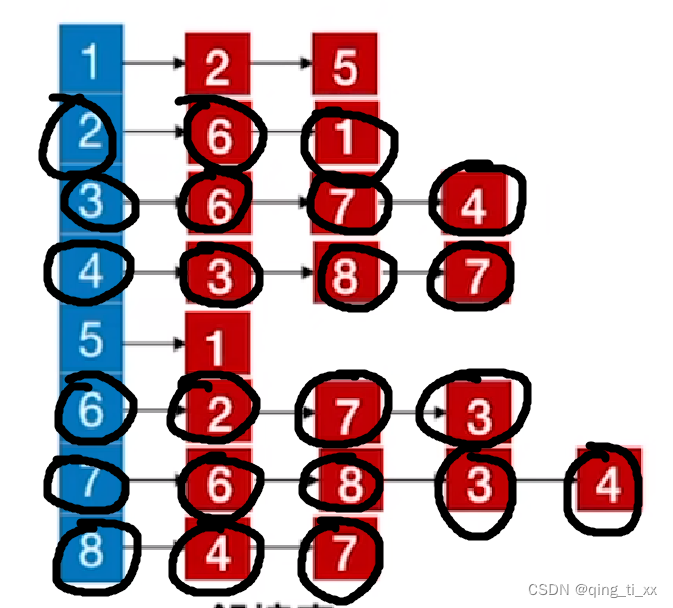
13、跳转至1,访问2(跳过),访问5;
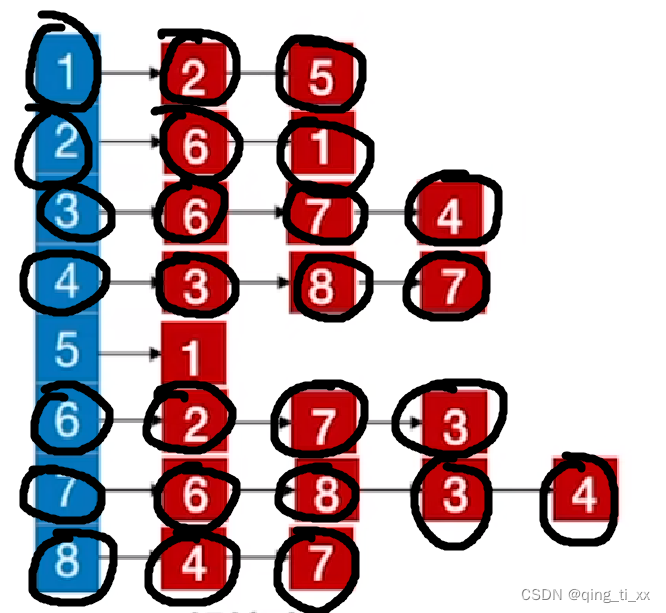
14、跳转至5,访问1,跳过;
至此,邻接表所有结点全部访问完毕。
四、深度优先生成树
五、深度优先生成森林
六、图的遍历与图的连通性
无向图:
有向图:
一、定义
1、深度优先遍历(Depth-First Search, DFS)是一种遍历或搜索图的算法。
2、该算法从图的某一个起始节点开始,递归地探索该节点的所有邻居节点,直到找出整个图的连通部分。
3、DFS使用了栈的数据结构来保存待访问的节点。
4、当访问一个节点时,我们将该节点入栈,并将其标记为已访问。
然后,如果该节点有未访问的邻居节点,我们就将邻居节点入栈并标记为已访问。
这个过程一直持续到栈为空为止。当栈为空时,我们就完成了整个图的深度优先遍历。
深度优先遍历通常用于解决以下问题:
- 检测一个无向图是否为连通图。
- 搜索一条路径,例如在迷宫中从起点到终点的最短路径。
- 找出一个无向图的所有连通分量。
深度优先遍历算法具有以下优点:
- 实现简单。
- 占用的空间相对较小,因为它只需要一个栈来保存待访问的节点。
- 适用于解决一些基于图的问题。
深度优先遍历算法的一个缺点是:
它可能会陷入无限循环中,因为它只是深度优先探索邻居节点,而不是考虑整个图的结构。这种缺点可以通过引入剪枝策略来解决,例如标记已访问的节点,或者设置搜索的深度限制。
二、代码
#include <iostream>
#include <vector>
using namespace std;
void DFS(int start, vector<vector<int>>& graph, vector<bool>& visited) {
visited[start] = true; // 标记当前节点为已访问
cout << start << " "; // 输出遍历到的节点
for (int i = 0; i < graph[start].size(); i++) {
int next = graph[start][i];
if (!visited[next]) { // 如果下一个节点未被访问
DFS(next, graph, visited); // 递归访问下一个节点
}
}
}
int main() {
// 构建一个图
vector<vector<int>> graph = {{1, 2}, {0, 3, 4}, {0, 5, 6}, {1}, {1}, {2}, {2, 7}, {6}};
vector<bool> visited(graph.size(), false); // 初始化所有节点为未访问状态
DFS(0, graph, visited); // 从节点0开始深度优先遍历
return 0;
}
空间复杂度:
最好情况:
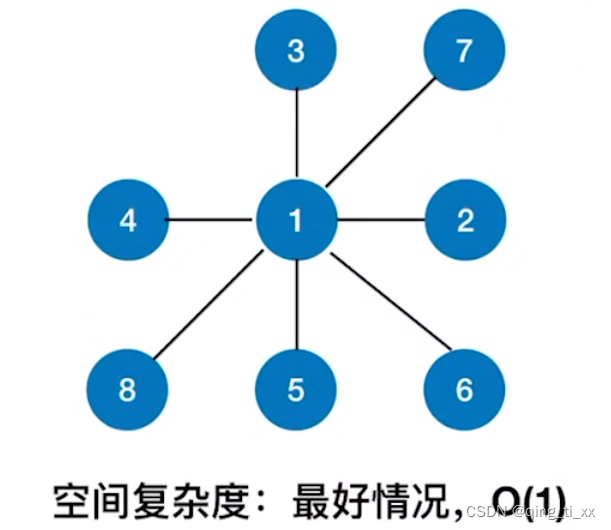
最坏情况:

时间复杂度:

邻接矩阵存储:
![]()
邻接表存储:
![]()
三、手动模拟深度优先遍历⭐⭐⭐⭐⭐
假如我们由如下邻接表:
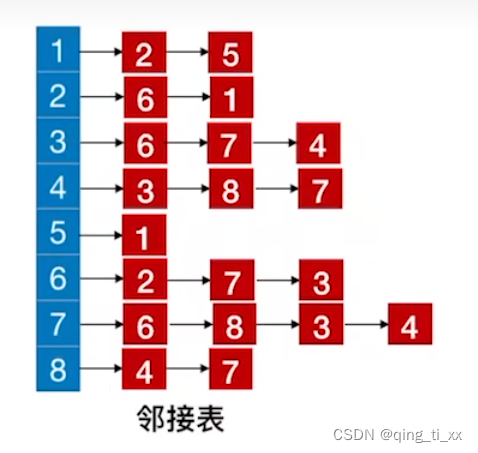
我们要得到从2开始的深度优先遍历序列。
1、首先访问结点2
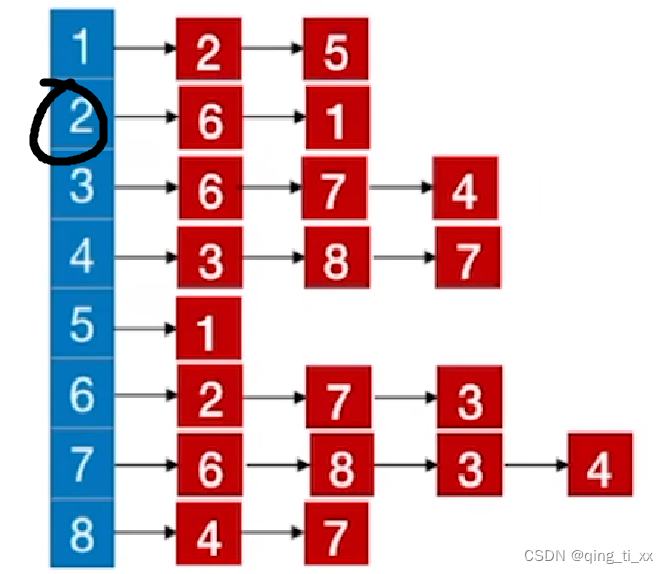
此时,遍历序列为

2、访问2的邻接点6
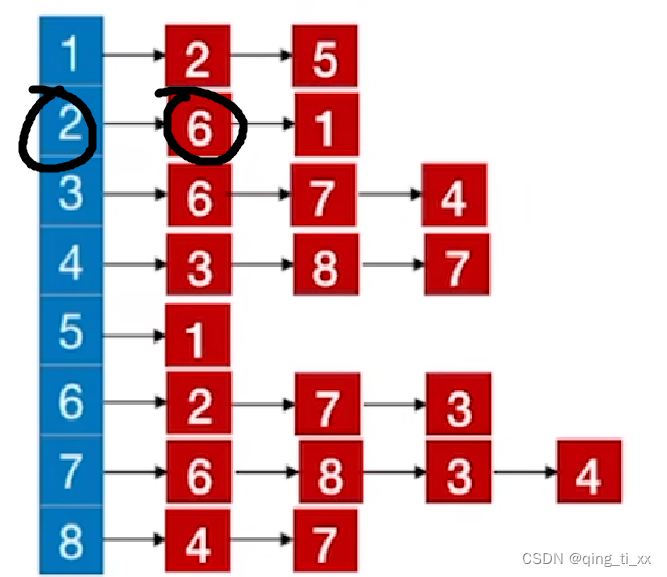
此时,遍历序列为

3、跳转到6,访问6的邻接结点,发现2已经被访问过了,于是访问7
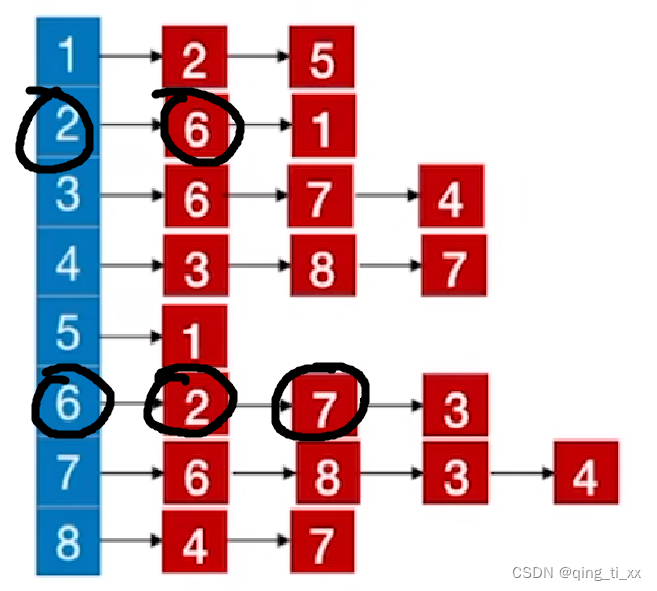
此时,遍历序列为

4、跳转到7,访问7的邻接结点,6被访问过了所以跳过,访问8
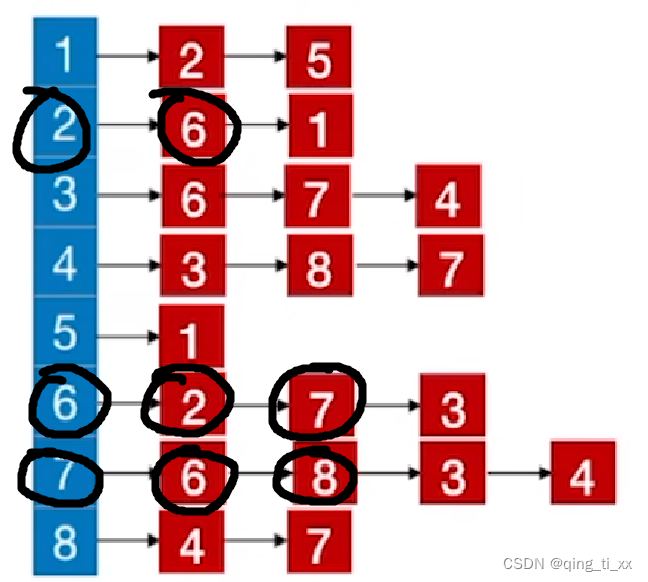
此时,遍历序列为

5、跳转到8,访问8的邻接结点,访问4
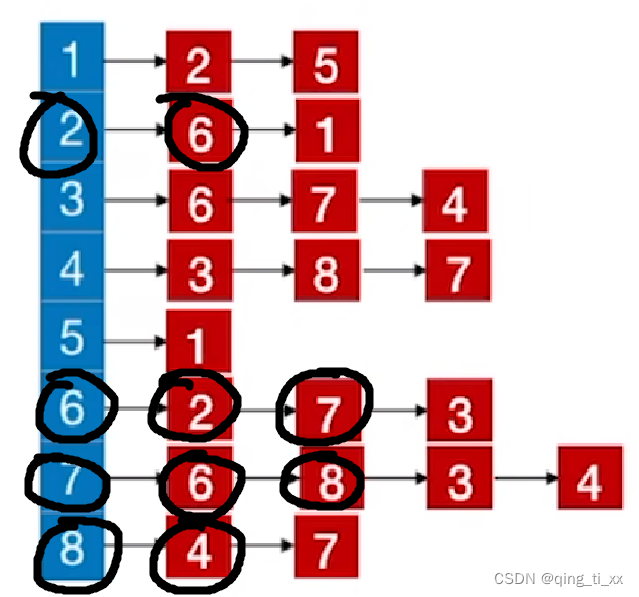
此时,遍历序列为
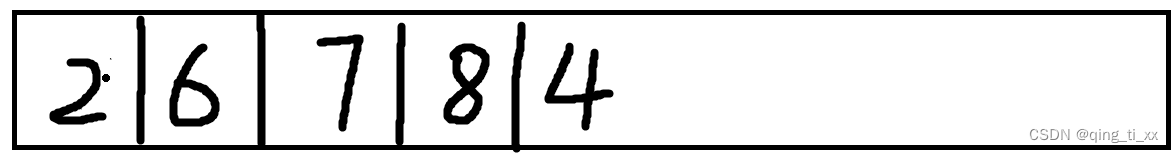
6、继续访问跳转到4,访问4的邻接结点,访问3
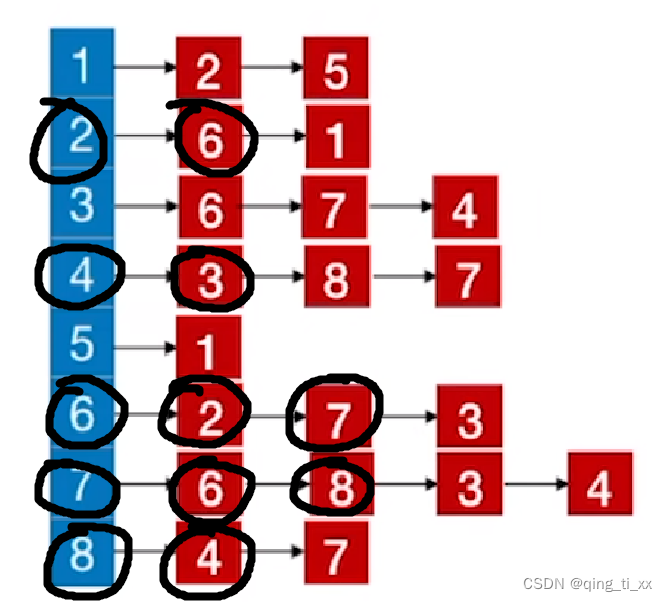
此时,遍历序列为
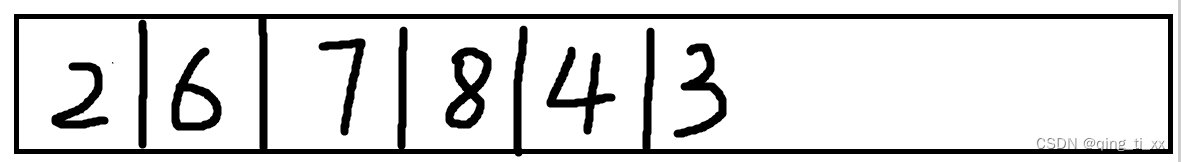
7、跳转到3,访问3的邻接结点,访问6,6被访问过了(跳过),访问7(跳过),访问4(跳过),由于3的邻接结点都被访问完了,所以返回上一级;
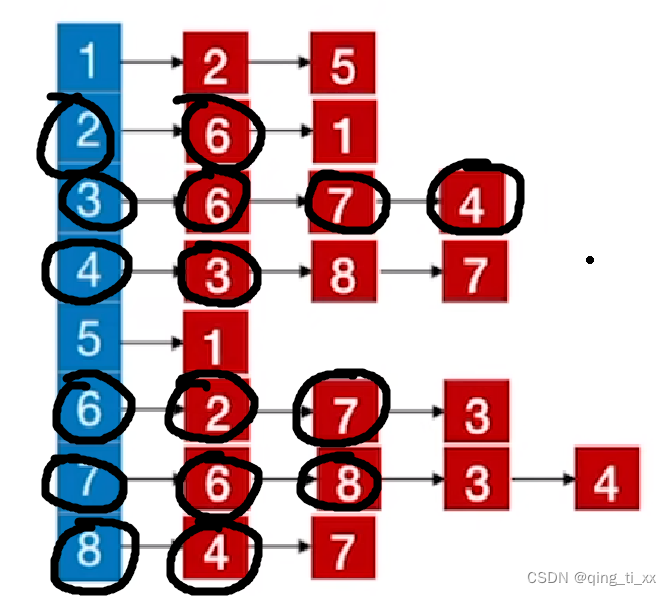
8、遍历4,访问8(跳过),访问7(跳过),返回上一级;
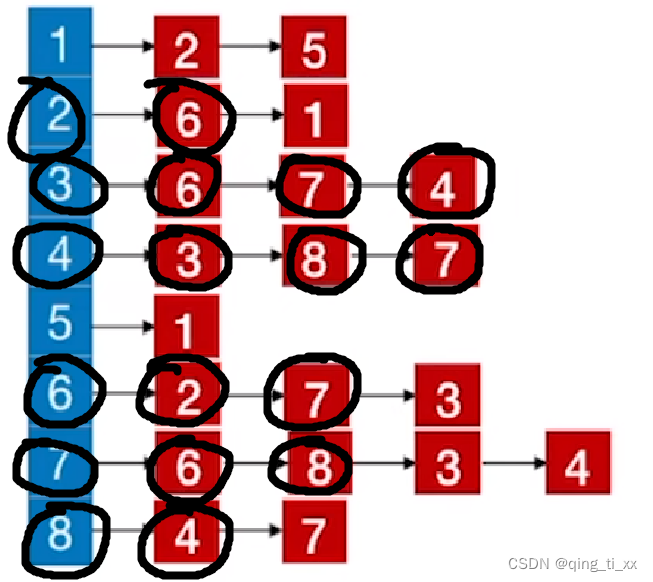
9、上一级是8,所以遍历8,访问7(跳过),返回上一级;
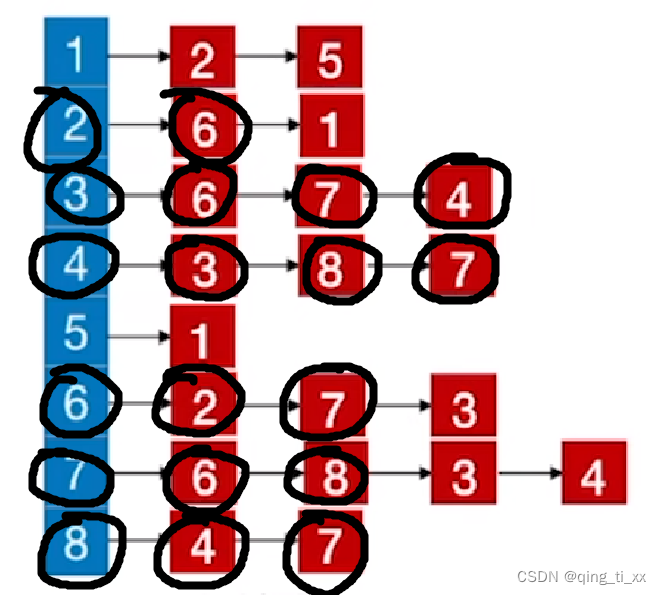
10、遍历7,访问3(跳过),访问4(跳过),返回上一级;
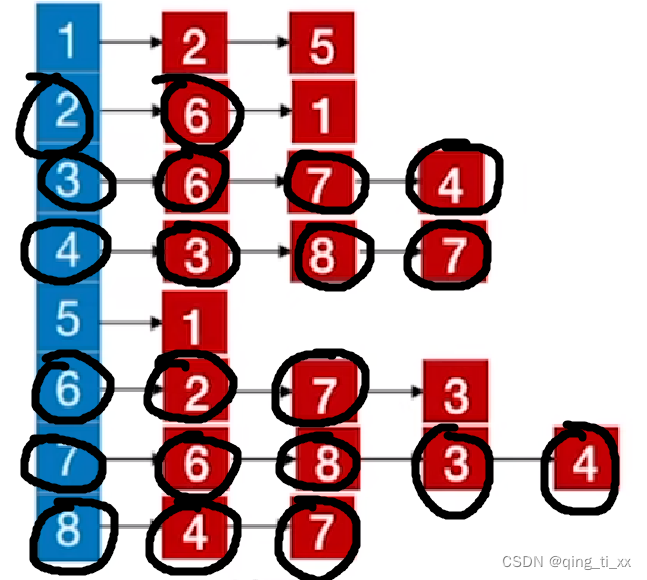
11、遍历6,访问3(跳过),返回上一级;
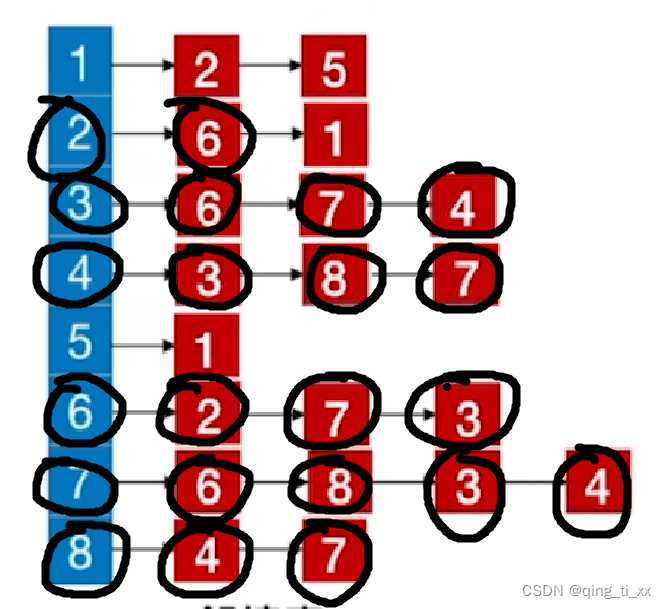
12、遍历2,访问1;
此时,遍历序列为

13、跳转至1,访问2(跳过),访问5;
此时,遍历序列为
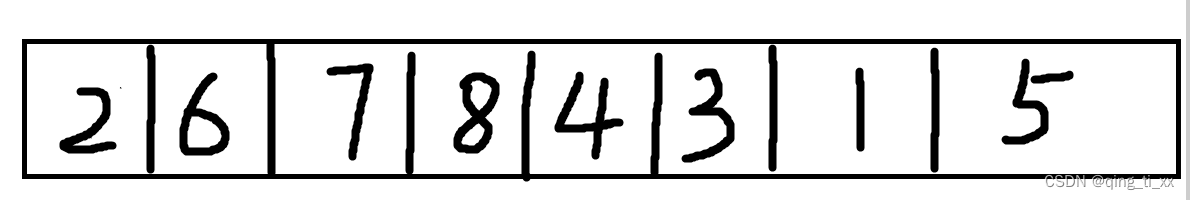
14、跳转至5,访问1,跳过;
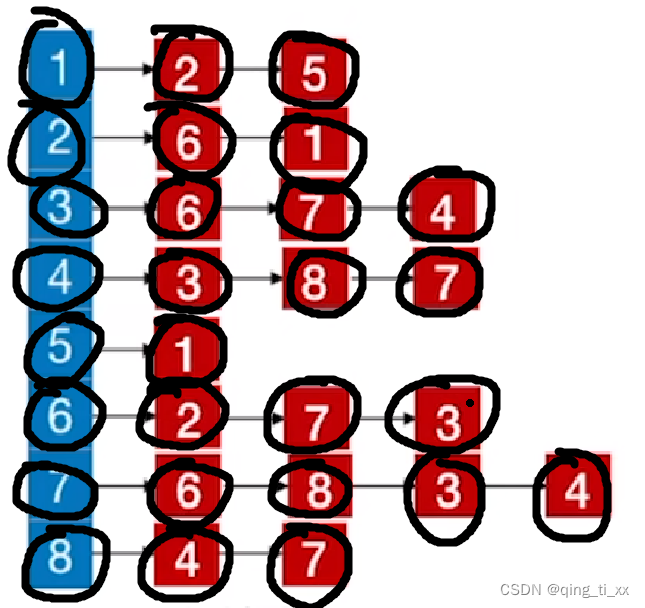
至此,邻接表所有结点全部访问完毕。
得到深度优先遍历序列为:2、6、7、8、4、3、1、5
四、深度优先生成树
与广度优先生成树相似,都是把每个结点第一次被访问的路径提取出来所生成的树,就是生成树
以下图为例:
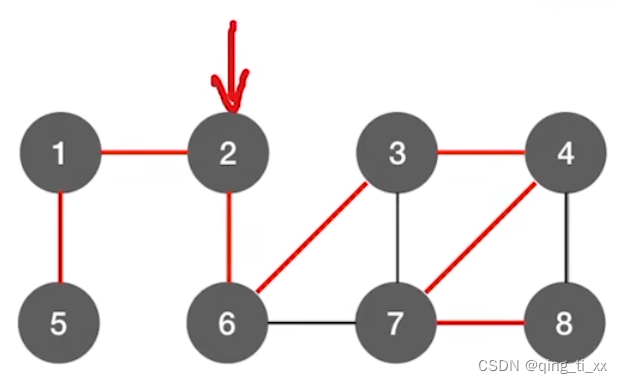
我们从2开始访问,把每个结点第一次被访问的路径标红,这就是生成树。
注意:

五、深度优先生成森林
我们多加一个图
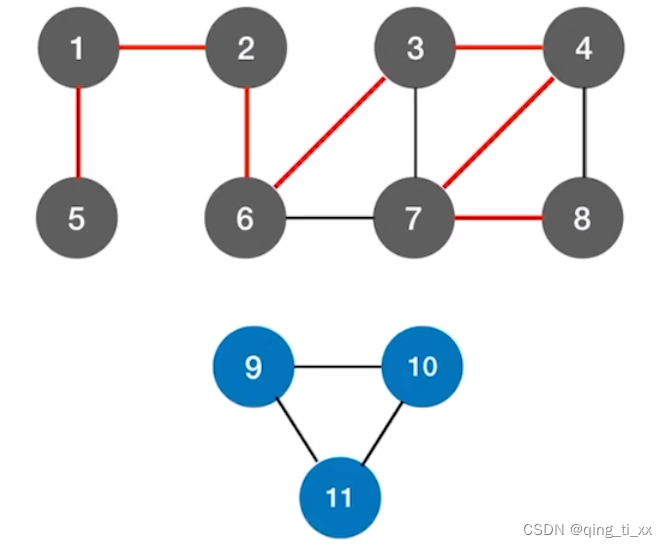
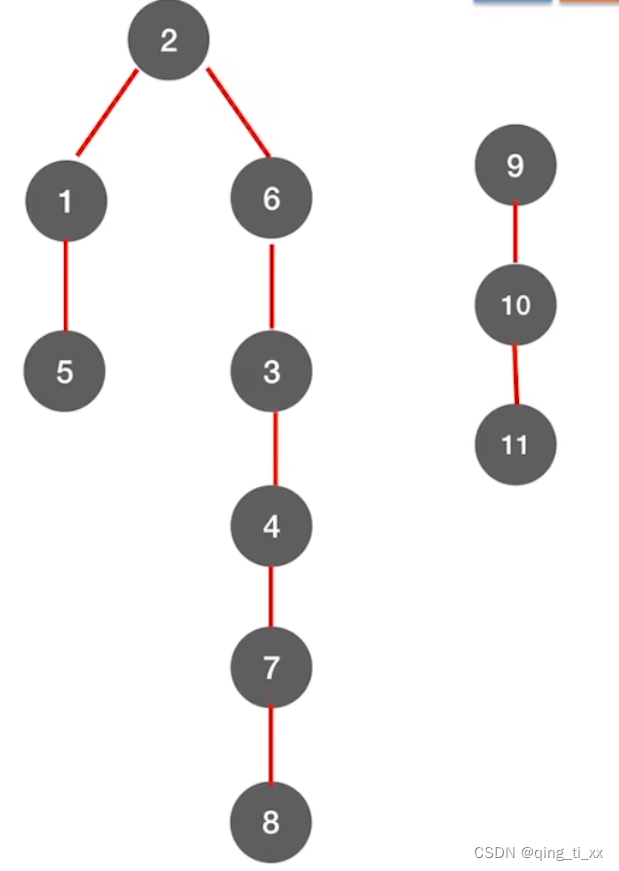
然后表示出它的深度优先生成树,写在一起,就是深度优先生成森林
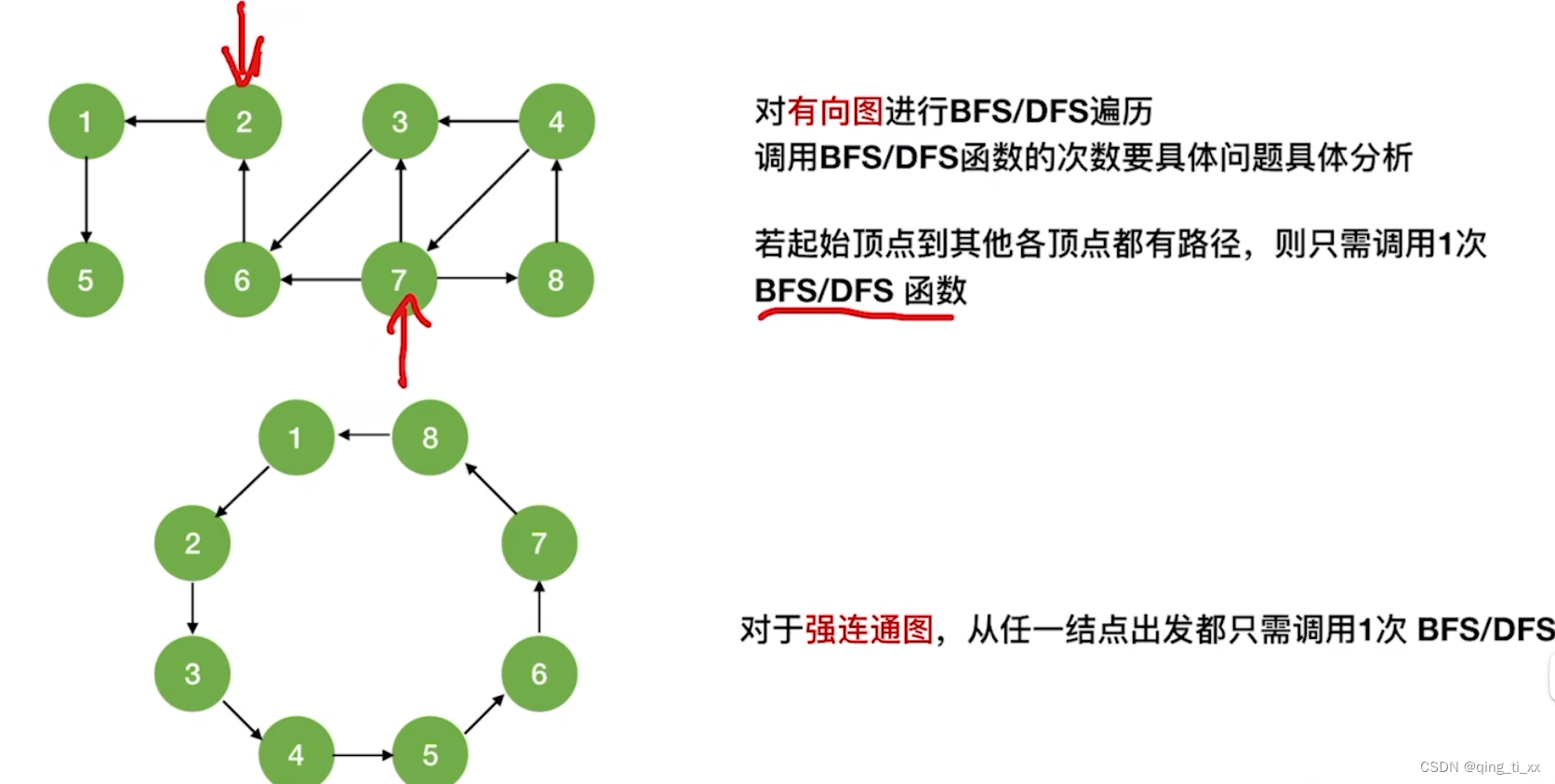
六、图的遍历与图的连通性
无向图:

有向图:
![[Qt]基础数据类型和信号槽](https://img-blog.csdnimg.cn/5e3bbac85e3f4c56801d12f932fc662d.png)