开篇词 | 从今天起，跨过“数据结构与算法”这道坎

边读边练，写代码时考虑性能方面的问题，进行时间、空间复杂度分析。

遇到问题，解决之后进行思考、研究透彻。

技术人成长的姿势：关注架构和技术趋势的概念、设计思想、实践为能力。

不管上层衍生出来多少新技术、新产品，都依赖于底层的基础知识，所以基础知识才是核心和本质。

基础知识包括：

• 数据结构与算法。
• 计算机组成原理。
• 操作系统。
• 计算机网络。
• 编译原理。
• 数据库原理。

基础知识决定技术高度和建造技术大楼的速度和质量。

学习的过程需要思考和时间，而不是死记硬背，思考怎么用？为什么需要？如何用？设计思想是什么？应用场景有哪些？

所有知识转化为能力的过程，都是逻辑思维的锻炼和动手能力的实践提升，而绝不是死记硬背，机械的重复记忆。

对于生活中遇到问题的态度和处理：
人生路上，我们会遇到很多的坎。跨过去，你就可以成长，跨不过去就是困难和停滞。而在后面很长的一段时间里，你都需要为这个困难买单。对于我们技术人来说，更是这样。既然数据结构和算法这个坎，我们总归是要跨过去，为什么不是现在呢？

数据结构和算法是一个普通程序员和一个优质高潜质程序员之间永远的区分线。

01 | 为什么要学习数据结构和算法？

面试，数据结构和算法基础知识是对长期潜力的考察。

算法思维将实际问题抽象为数学问题，然后用计算机将数学问题用代码进行表示和处理。

学习任何知识如果不是为了去应用解决实际问题，那便毫无意义。

多刁难自己，多给自己提问，然后去解决，在解决的过程中就可以学到更多新知识。简而言之就是在学习方面不要放过自己，随时挑自己的刺。

即使是直接调用类库接口，也至少应该知道根据自己的业务应该调用哪个类的哪些接口，更深层次来说，你经常调用的接口难道就没有兴趣了解一些实现？这些实现凭什么可以被放在标准库中使用？实现的时候有没有什么缺点？如果让你实现，你是否实现的比标准库好？不断给自己提问，然后去解决，解决的过程就会学到更多知识，自己的知识地图不断扩大，深度越深越能接触到底层最本质的原理，逻辑思维能力和解决问题的能力就会不断提升。

如果自己经常使用的东西，都不知道该如何取用，都不知道实现和原理，那是多么可怕的事情。

写出达到开源水平的框架才是目标。

高手之间的竞争是细节的竞争：
算法够不够优化—时间复杂度，数据存取效率是不是够高—响应时间，内存是不是足够节省—空间复杂度。

做事情需要有难度梯度，需要思考，在解决问题的过程中提升能力。走出舒适区，不断锻炼自己。

即学即用，即用即学。

在实践中遇到问题去思考，然后带着问题去学习，是非常高效的学习方法。

学习数据结构和算法的目的：

• 建立时间、空间复杂度意识，写出高质量的代码，提升编程能力。
• 能够设计基础架构。
• 训练逻辑思维。
• 积攒人生经验。
• 长期看来，大脑的思考能力是个人最重要的核心竞争力，算法是为数不多的能够有效训练大脑思考能力的途径之一。
• 获得工作汇报，实现价值。
• 完善人生。

掌握了数据结构与算法，看待问题的深度，解决问题的角度就会完全不一样。不只是编程方面，生活中的各个方面，遇到各种问题，会因为你的逻辑思维能力获得锻炼和提升而处理的更好。

02 | 如何抓住重点，系统高效地学习数据结构与算法？

生活中遇到的大多数事情，要么已有解决方案，要么有其他领域可以借鉴。如果遇到一个问题是原创问题，那么就自己动脑子解决它，这种解决的过程带来能力和价值的提升是飞速的，也会给自己带来回报。

思考工作中会遇到的技术和框架，也可以不断去了解当下最火的技术，然后剖析背后的原理本质和设计思想。

编程就是实用派，有没有用，效果如何，动手实践才是提升的本质。

数据结构：一组数据在内存中的存储结构。
算法：操作特定数据结构的步骤。（特定理解为数据结构和算法存在适配关系。）

数据结构和算法是前人的智慧，经过求证和实践检验，可以帮助我们高效地解决很多实际开发中的问题。

选择正确的数据结构会让算法变得简单和高效，有些算法只能在特定的数据结构上操作。

思考实际应用场景？是什么？为什么？怎么实现的？怎么使用？设计思想是什么？

写代码的时候时刻要考虑时间复杂度和空间复杂度。

本质上在工作生产中，到底选取哪种数据结构和算法，是由复杂度分析决定的，我们剖析很多开源代码，剖析STL本质都是为了研究设计思想和实现对于时间复杂度和空间复杂度是如何影响的。

为什么说复杂度分析是数据结构和算法的精髓，就是因为所有的数据结构和算法都需要考虑时间复杂度和空间复杂度，对于我们在实际开发工作中有着绝对的影响，实践过程中就是不断思考时间复杂度和空间复杂度更低的数据结构和算法，不断提高性能和节省空间。

数据结构和算法解决的问题：更快运行，更省内存。

数据结构和算法知识图：

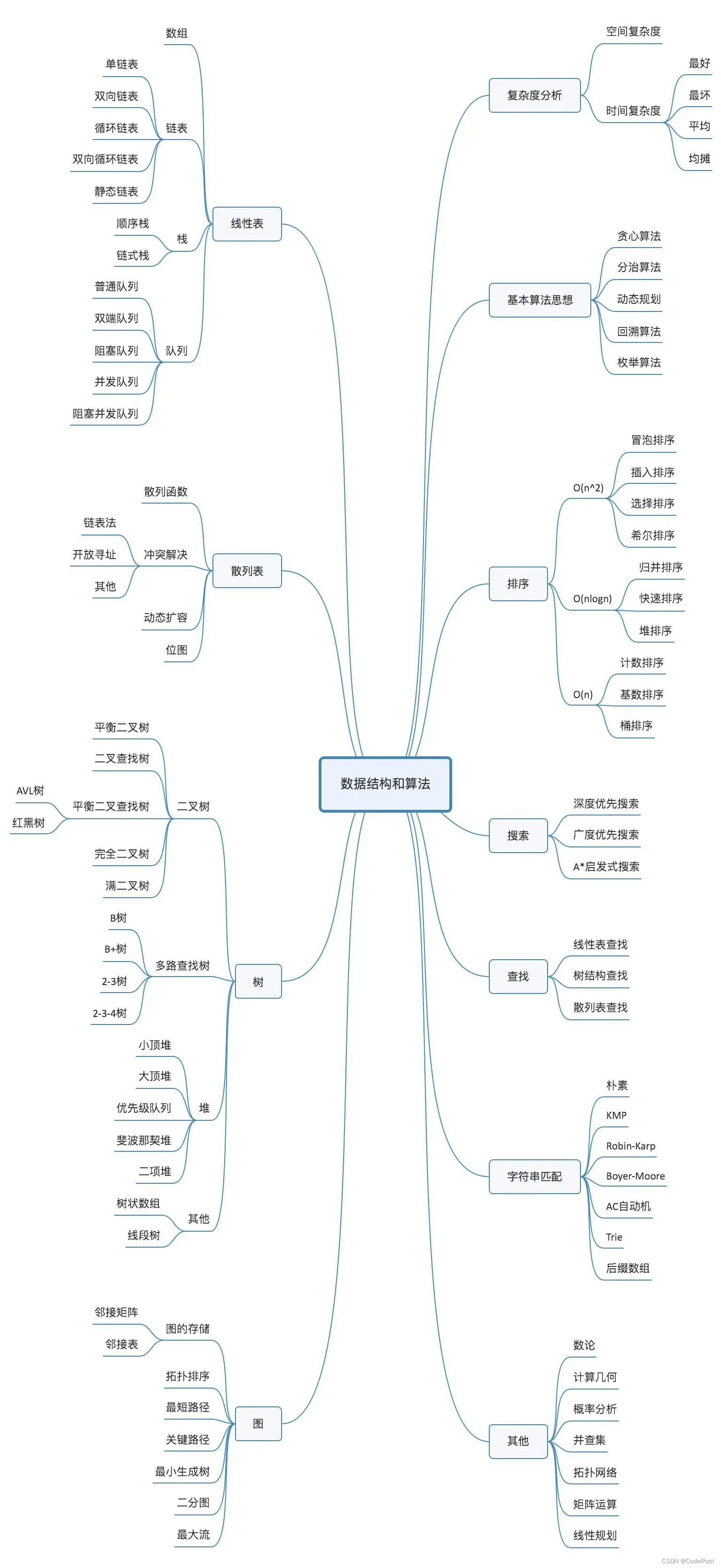
10个常用数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie树。
10个常用算法：排序、递归、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法。

从学习的本质来说，任何学习都是不是死记硬背，而是应用将知识转化为能力，学习数据结构和算法更是如此，多辩证思考，多给自己提问：为什么会有？有什么特点？解决了什么问题？有什么应用场景？如何实现的？等，然后不断解决问题，在解决问题的过程中学习更多，锻炼自己的能力。

简单小结就是：边学边练，带着问题学习，即用即学，即学即用。多问、多思考、多交流、多动手实践。完全弄懂，避免一知半解。

学习的过程中，能力是不断迭代式螺旋上升的，遇到问题和不懂的是非常正常的，你要给自己留有容错空间。很多问题会随着你知识和能力不断提升和豁然开朗。

03 | 复杂度分析（上）：如何分析、统计算法的执行效率和资源消耗？

数据结构和算法解决的是：如果在计算机内存更快时间、更省空间的解决问题。

从执行时间和占用空间两个维度来评估数据结构和算法的性能。

用时间复杂度和空间复杂度来描述性能，二者统称为复杂度。

复杂度描述的是算法执行时间（或占用内存空间）与数据规模的的增长关系。

复杂度分析不依赖于执行环境，成本低，效率高，易操作，指导性强。

掌握复杂度分析，编写出性能更优的代码。

算法的执行时间与每行代码的执行次数成正比，T(n) = O(f(n))，T(n)表示算法执行总时间，f(n) 表示每行代码的执行总次数，n表示数据规模。

时间复杂度（空间复杂度）描述算法的执行时间（额外占用空间）随数据规模增长变化的趋势。常量阶、低阶、系数对增长趋势不产生决定性影响，分析是可以忽略。

时间复杂度：单段代码看高频率（循环），多段代码取最大（单循环和多重循环取多重循环），嵌套代码求乘积（递归，多重新循环等），多个规模求加法（两个参数控制两个循环次数，取二者时间复杂度相加）。

复杂度级别：
多项式比例增长：O(1)，O(logn)，O(n)，O(nlogn)，O(n ^ 2)，O(n ^ 3)。
非多项式暴增：O(2^n)，O(n!)。

多练习分析时间复杂度。

遇到一个新的思路：数据结构横向解决运算时间快和空间省的问题，纵向解决架构和抽象的问题（数据结构和算法的泛型）。

所有数据结构和算法都会涉及时间复杂度和空间复杂度的问题。

为什么需要复杂度分析

先进行良好的设计，然后根据设计进行分析改进，最后再去执行。

事后统计法存在局限性：

• 测试结果依赖环境。
• 测试结果受数据规模影响很大。

举例：计算乘法。测试环境其中影响非常大的就是硬件，对于不同的指令集系统就会对结果有影响，乘法

通过时间复杂度、空间复杂度分析，进行粗略计算算法的执行效率。

很多算法都是适配固定的数据结构和应用场景，没有任何场景都是适用的完美算法。

大 O 复杂度表示法

算法的执行效率：算法代码执行时间越短，效率越高。

 int cal(int n) {
   int sum = 0;
   int i = 1;
   for (; i <= n; ++i) {
     sum = sum + i;
   }
   return sum;
 }

从CPU的角度看，每一个语句都执行着类似的操作：读数据-运算-写数据。
假设每个语句的执行时间都是一样的为unit_time。

第2行执行 1 次。
第3行执行 1 次。
第4行 i <= n 执行 n + 1次，++i 执行 n 次。
第5行执行了 n 次。

第7行执行 1 次。
这段代码总的执行时间：(3n + 4) * unit_time。

 int cal(int n) {
   int sum = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1;
     for (; j <= n; ++j) {
       sum = sum +  i * j;
     }
   }
 }

第2行执行 1 次。
第3行执行 1 次。
第4行执行 1 次。
第5行 i <= n 执行 n + 1次，++i 执行 n 次。
第6行执行 n 次。
第7行 j <= n 执行 n ^ 2 + 1次，++j 执行 n ^ 2 次。
第8行 n ^ 2 次。
这段代码总的执行时间：(3n ^ 2 + 3n + 5) * unit_time。

所有代码的执行时间 T(n) 与每行代码的执行次数 f(n) 成正比。

总结规律：

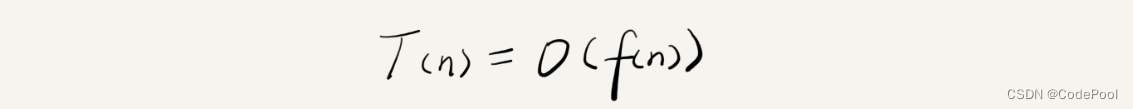
T(n)：代码执行时间。
n：数据规模。
f(n)：每个语句执行总次数。
O：代码执行时间 T(n) 和 f(n) 表达式成正比。

上面两个例子用大 O 时间复杂度表示为：
T(n) = O(3n + 4)
T(n) = O(3n ^ 2 + 3n + 5)

大 O 时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），我们最终想要的肯定是随数据规模时间和空间增加速度最慢的复杂度。

公式中的低阶、常量、系数三部分并不左右增长趋势，可以忽略。
上面两个例子用忽略后的大 O 时间复杂度表示为：
T(n) = O(n)
T(n) = O(n ^ 2)

时间复杂度分析

只关注循环次数最多的一段代码

 int cal(int n) {
   int sum = 0;	//常量
   int i = 1;	//常量
   for (; i <= n; ++i) {	//n
     sum = sum + i;	//n
   }
   return sum;	//常量
 }

T(n) = O(n)。

加法法则：总复杂度等于量级最大的那段代码的是复杂度

int cal(int n) {
   int sum_1 = 0;	//常量
   int p = 1;	//常量
   for (; p < 100; ++p) {	//n
     sum_1 = sum_1 + p;	//n
   }

   int sum_2 = 0;	//常量
   int q = 1;	//常量
   for (; q < n; ++q) {	//n
     sum_2 = sum_2 + q;	//n
   }
 
   int sum_3 = 0;	//常量
   int i = 1;	//常量
   int j = 1;	//常量
   for (; i <= n; ++i) {	//n
     j = 1; 	//n
     for (; j <= n; ++j) {	//n^2
       sum_3 = sum_3 +  i * j;	//n^2
     }
   }
 
   return sum_1 + sum_2 + sum_3;	//常量
 }

T(n) = O(n^2)。

将规律抽象成公式：
T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))

乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

int cal(int n) {
   int ret = 0; 	//常量
   int i = 1;	//常量
   for (; i < n; ++i) {	//n
     ret = ret + f(i);	//n^2
   } 
 } 
 
 int f(int n) {
  int sum = 0;	//常量
  int i = 1;	//常量
  for (; i < n; ++i) {	//n
    sum = sum + i;	//n
  } 
  return sum;//常量
 }

T(n) = T1(n) * T2(n) = O(n*n) = O(n2)。

几种常见时间复杂度实例分析

多项式复杂度量级：：O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )

非多项式复杂度量级（ NP（Non-Deterministic Polynomial，非确定多项式）问题。）：O(2n) 和 O(n!)。
非多项式复杂度量级是非常低效的。

O(1)

 int i = 8;
 int j = 6;
 int sum = i + j;

只要代码的执行时间不随 n 的增大而增长，时间复杂度就是 O(1)。
一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是Ο(1)。

O(logn)、O(nlogn)

 i=1;
 while (i <= n)  {
   i = i * 2;
 }

求取了多少次 x
2^x = n
x = log2n

时间复杂度为：O(log2n)。

 i=1;
 while (i <= n)  {
   i = i * 3;
 }

log3n 等于 log32 * log2n

O(log3n) = O(C * log2n)

C=log32 是一个常量，可以忽略： O(Cf(n)) = O(f(n))

O(log2n) 等于 O(log3n)

对数阶时间复杂度里面，忽略底，同意表示为 O(logn) 。

O(m+n)、O(m*n)

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

无法事先评估 m 和 n 那个量级更大。时间复杂度：O(m +n)。

通用规则：
T1(m) + T2(n) = O(f(m) + g(n))。

乘法规则继续有效：
T1(m)*T2(n) = O(f(m) * f(n))。

空间复杂度分析

void print(int n) {
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }

  for (i = n-1; i >= 0; --i) {
    print out a[i]
  }
}

第2行，申请1个空间存储变量，常数阶。
第三行，申请大小为 n 的数组，空间复杂度为 O(n)。

整段代码空间复杂度为：O(n)。

内容小结

常见复杂度从底到高：：O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )

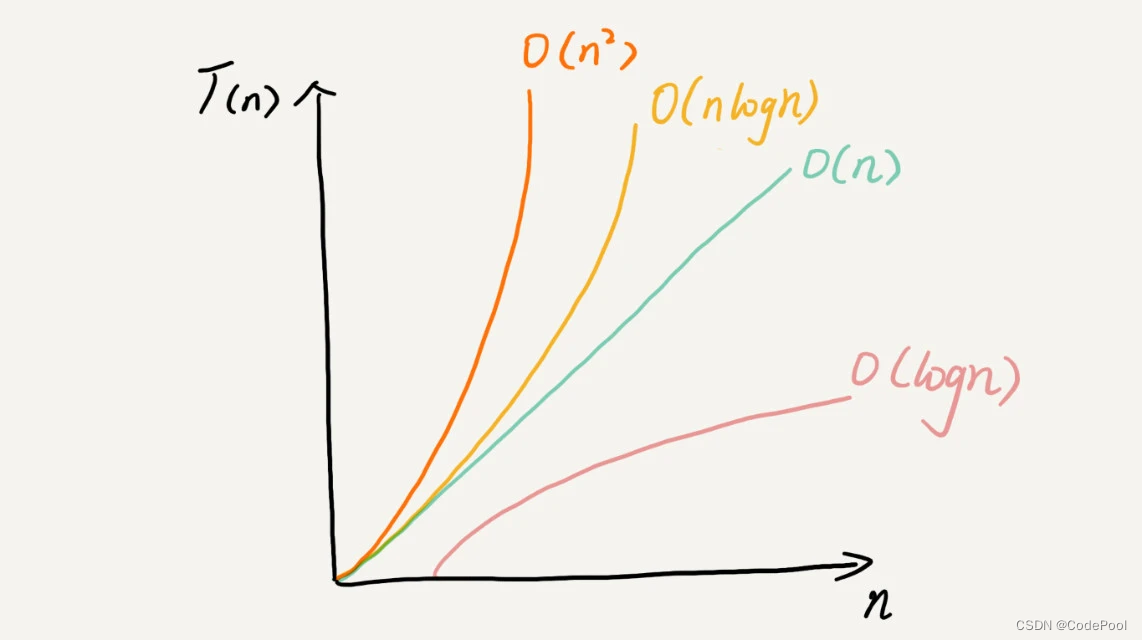
复杂度分析并不难，关键在于多练。

课后思考

有人说，我们项目之前都会进行性能测试，再做代码的时间复杂度、空间复杂度分析，是不是多此一举呢？而且，每段代码都分析一下时间复杂度、空间复杂度，是不是很浪费时间呢？你怎么看待这个问题呢？

我不认为是多此一举，渐进时间，空间复杂度分析为我们提供了一个很好的理论分析的方向，并且它是宿主平台无关的，能够让我们对我们的程序或算法有一个大致的认识，让我们知道，比如在最坏的情况下程序的执行效率如何，同时也为我们交流提供了一个不错的桥梁，我们可以说，算法1的时间复杂度是O(n)，算法2的时间复杂度是O(logN)，这样我们立刻就对不同的算法有了一个“效率”上的感性认识。

当然，渐进式时间，空间复杂度分析只是一个理论模型，只能提供给粗略的估计分析，我们不能直接断定就觉得O(logN)的算法一定优于O(n), 针对不同的宿主环境，不同的数据集，不同的数据量的大小，在实际应用上面可能真正的性能会不同，个人觉得，针对不同的实际情况，进而进行一定的性能基准测试是很有必要的，比如在统一一批手机上(同样的硬件，系统等等)进行横向基准测试，进而选择适合特定应用场景下的最有算法。

综上所述，渐进式时间，空间复杂度分析与性能基准测试并不冲突，而是相辅相成的，但是一个低阶的时间复杂度程序有极大的可能性会优于一个高阶的时间复杂度程序，所以在实际编程中，时刻关心理论时间，空间度模型是有助于产出效率高的程序的，同时，因为渐进式时间，空间复杂度分析只是提供一个粗略的分析模型，因此也不会浪费太多时间，重点在于在编程时，要具有这种复杂度分析的思维。

懂得了时间复杂度、空间复杂度分析之后，在写代码的时候，就会去尽可能寻找最优的算法。而性能测试，则是代码写完之后，才能进行的。只能是事后的。

上述回答来源于留言区的置顶回答，写的真好，把我想说又说不好的话都说了出来。

18 | 散列表（上）：Word文档中的单词拼写检查功能是如何实现的？

散列思想

散列表，HashTable，哈希表，Hash表，都是同一个表达。

散列表用的是数组支持按照下标随机访问数据的特性，所以散列表其实就是数组的一种扩展。

将 键 key（或者关键字），通过散列函数（或Hash函数、哈希函数）映射计算得到散列值（或Hash值、哈希值），将散列值作为数组下标。

TUTU

总结规律：散列表用的就是数组支持按照下标随机访问的时候，时间复杂度是 O(1) 的特性。我们通过散列函数把元素的键值映射为下标，然后将数据存储在数组中对应下标的位置。当我们按照键值查询元素时，我们用同样的散列函数，将键值转化数组下标，从对应的数组下标的位置取数据。

散列函数

定义成 hash(key)，其中 key 表示元素的键值，hash(key) 的值表示经过散列函数计算得到的散列值。

散列函数设计的基本要求：

1. 散列函数计算得到的散列值是一个非负整数；（数组下标从0开始）
2. 如果 key1 = key2，那 hash(key1) == hash(key2)；
3. 如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)。

第三个条件，在真实的情况下，要想找到一个不同的 key 对应的散列值都不一样的散列函数，几乎是不可能的。
像业界著名的MD5、SHA、CRC等哈希算法，也无法完全避免这种散列冲突。
因为数组的存储空间有限，也会加大散列冲突的概率。

MD5哈希算法：

SHA哈希算法：

CRC哈希算法：

散列冲突

开放寻址法

开放寻址法的核心思想是，如果出现了散列冲突，我们就重新探测一个空闲位置，将其插入。