生成整数序列字典序的r-组合算法
- 一、PPT效果展示
- 二、问题
- 2.1 简述
- 2.2 算法简述
- 2.3 例子
- 三、PPT实现
一、PPT效果展示

二、问题
2.1 简述
给定一个整数序列 (1,2,3,…n),输出其所有字典序的r-组合,注意事项:
- 所有组合不能重复,每个组合中的元素顺序需为字典序 (从小到大)
- 所有组合呈字典序 (后一组合 > 前一组合)
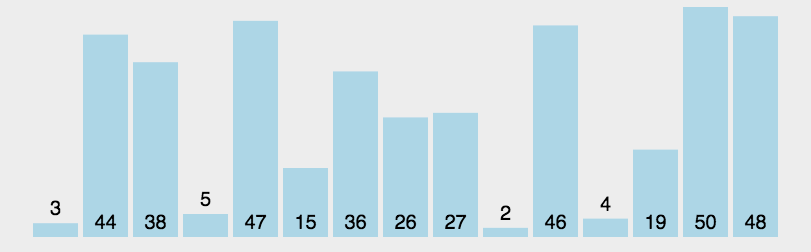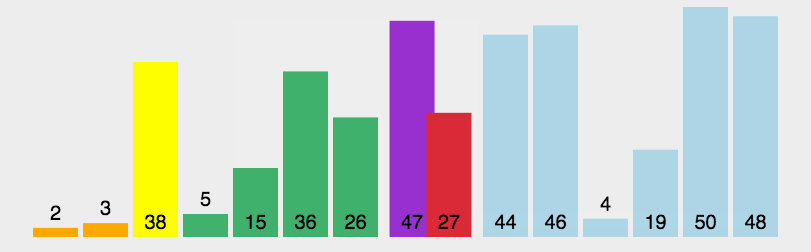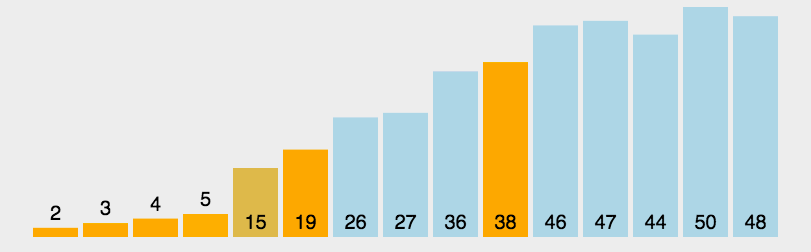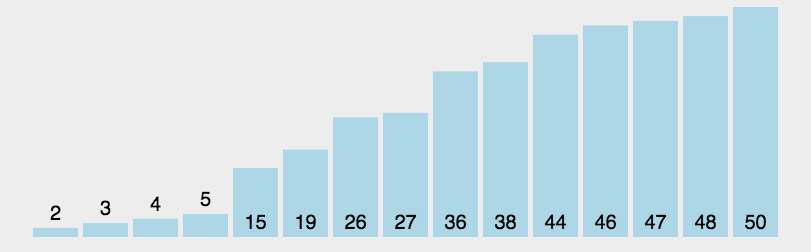
例:给定整数序列123456,求其4-组合
开始组合:1234
中间组合:1235,1236,1245,…
结束组合:3456
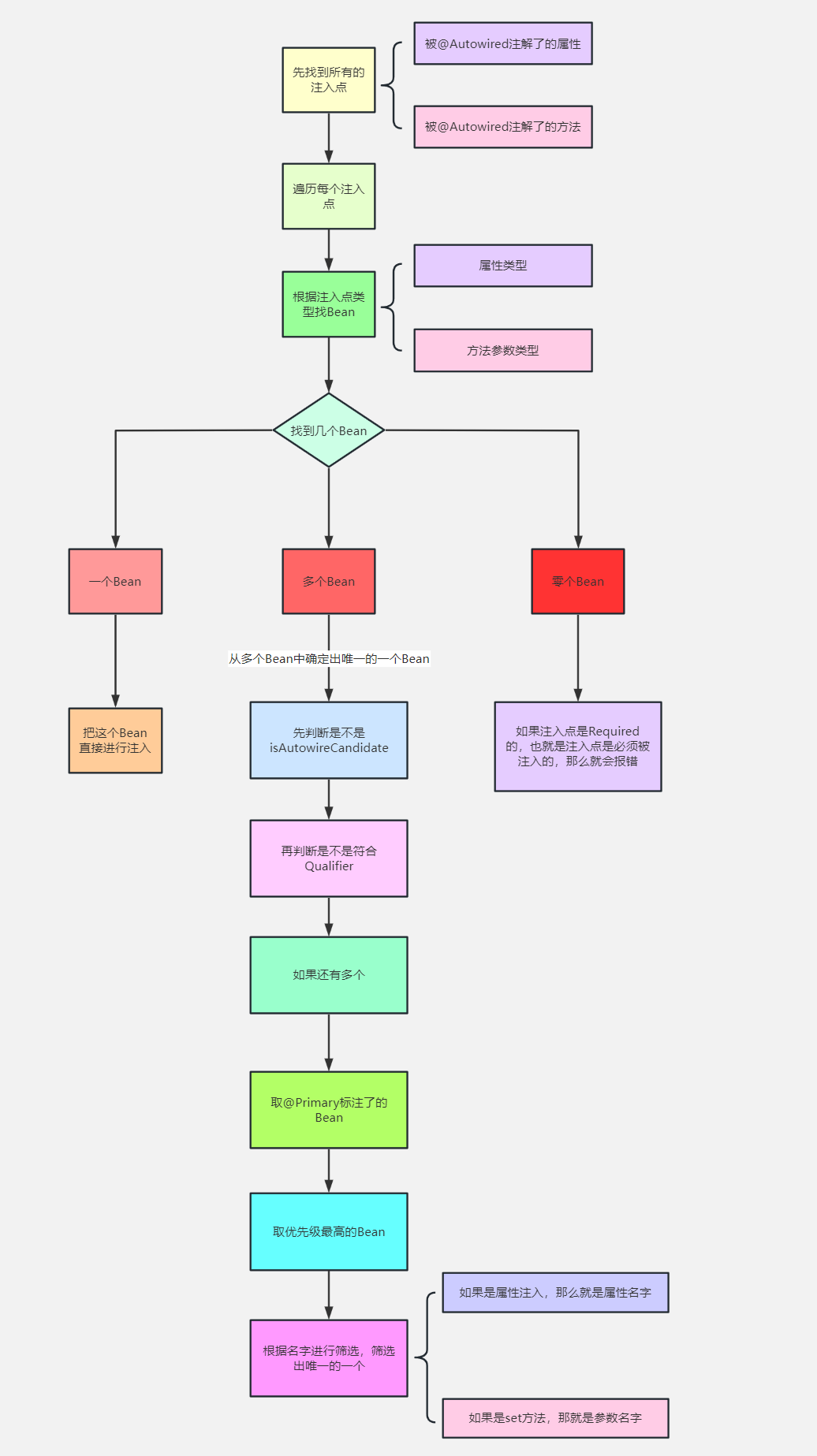
2.2 算法简述
给定一个整数序列(1,2,3,...n),其r-组合:
- 其必从{ 1 , 2 , . . . , r 1,2,...,r 1,2,...,r}开始,到{ n − r + 1 , . . . , n − 1 , n n-r+1,...,n-1,n n−r+1,...,n−1,n}结束
- 存在最大的一个整数 k ∈ { 1 , . . . , r } k\in \{1,...,r\} k∈{1,...,r},使得 A k + 1 ≤ n A_k + 1 \leq n Ak+1≤n 且 A k ∉ A A_k\notin A Ak∈/A ( A A A为当前组合, A k A_k Ak不属于当前组合)
- 新的组合
A
=
A =
A= {
A
1
,
.
.
.
,
A
k
−
1
,
A
k
+
1
,
.
.
.
,
A
k
+
r
−
k
+
1
A_1, ..., A_{k-1}, A_k+1, ..., A_k+r-k+1
A1,...,Ak−1,Ak+1,...,Ak+r−k+1}
其中, A 1 , . . . , A k − 1 A_1, ..., A_{k-1} A1,...,Ak−1是上一个组合的前一部分,新的组合从 A k A_k Ak开始更新
(个人理解)核心思想就是:由于现组合中的元素为字典序,选取最大的
k
k
k以及使用
A
k
+
1
,
A
k
+
2
,
.
.
.
A_k + 1, A_k+2, ...
Ak+1,Ak+2,... 替换
A
k
A_k
Ak及其后的元素,即可保证替换后依旧为字典序,且刚好比前一组合大“一点”
2.3 例子
例:整数序列1-6的4-组合,从1236 -> 1245:
A
=
A =
A= {
A
1
=
1
,
A
2
=
2
,
A
3
=
3
,
A
4
=
6
A_1=1, A_2=2, A_3=3, A_4=6
A1=1,A2=2,A3=3,A4=6}
- 若 k = 4 k=4 k=4, A 4 = 6 A_4 = 6 A4=6, A 4 + 1 > 6 A_4 + 1 > 6 A4+1>6,不符合条件。
- 存在最大的 k = 3 k=3 k=3,使得 A 3 + 1 = 4 A_3+1 = 4 A3+1=4,4小于6且不属于1236。
- 新的组合从
A
3
A_3
A3开始更新,即 {
A
1
,
A
2
,
A
3
+
1
,
A
3
+
4
−
3
+
1
A_1,A_2,A_3+1,A_3+4-3+1
A1,A2,A3+1,A3+4−3+1} =
{ 1 , 2 , 3 + 1 , 3 + 4 − 3 + 1 1, 2 ,3+1, 3+4-3+1 1,2,3+1,3+4−3+1} = { 1 , 2 , 4 , 5 1,2,4,5 1,2,4,5}
三、PPT实现
可到博客顶端 or 通过此链接 进入资源页下载完整PPT,放映即可用
亦可自行开发:在PPT左上角选择开发工具
主要控件:文本框 和 按钮
核心源码:
Public Sub F()
s_all = T_in.Text
n = Len(T_in.Text)
num = T_num.Text
s = L_c.Caption
k = 0
ak = 0
flag = 0
' 计算k和Ak
For i = 1 To num
flag = 1
' 如果大于n 则直接退出
a = Mid(s, i, 1) + 1
If (Val(a) > n) Then
Exit For
End If
For j = i To num
' 如果不符合条件 标志位set为0 跳出循环
b = Mid(s, j, 1)
If (StrComp(a, b, 1) = 0) Then
flag = 0
Exit For
End If
Next j
If StrComp(flag, 1, 0) = 0 Then
k = i
End If
Next i
L_k.Caption = k
L_ak.Caption = Mid(s, k, 1)
ak = L_ak.Caption
' 下一个组合
For i = num To k Step -1
'Dim tmp As String
'tmp = ak - k + 1 + i s_all
's = Replace(s, Mid(s, i, 1), Mid(s_all, ak - k + 1 + i, 1))
Mid(s, i, 1) = Mid(s_all, ak - k + 1 + i, 1)
Next i
L_next.Caption = s
End Sub
Private Sub B_next_Click()
s_all = T_in.Text
n = Len(T_in.Text)
num = T_num.Text
L_c.Caption = L_next.Caption
T_show = T_show + L_c.Caption + vbCr + vbLf
If StrComp(L_c.Caption, Mid(s_all, n - num + 1, num), 1) = 0 Then
MsgBox "已经是最后一个组合了"
Exit Sub
End If
Call F
'current = L_c.Caption
'MsgBox current
'MsgBox num
'current = Replace(current, Mid(current, 1, 1), Mid(s, 2, 1))
'MsgBox current
End Sub
Private Sub B_s_Click()
s = T_in.Text
num = T_num.Text
L_c.Caption = Mid(s, 1, num)
T_show = ""
T_show = T_show + L_c.Caption + vbCr + vbLf
Call F
End Sub
Private Sub T_show_Change()
End Sub
可参考的C源码
r-组合: https://blog.csdn.net/ld326/article/details/84341452