1.什么是二叉排序树

二叉排序树（Binary Sorting Tree）又称二叉搜索树（Binary Search Tree），是一种特殊结构的二叉数，作为一种排序和查找的手段，对应有序表的对半查找，通常亦被称为数表。其定义也是递归的。

二叉排序树的定义：
每个节点都有一个作为搜索依据的关键码（key），所有节点的关键码互不相同；
二叉排序树或者是空树或者是具有下述性质的二叉数，
	①其左子树上所有结点的数据值均小于根结点的数据值；
	②右子树上所有结点的数据值均大于根结点的数据值；
	③左子树和右子树又各是一棵二叉排序树。
二叉排序树用中序遍历就可以得到由小到大的有序序列

2.二叉排序树的数据结构

2.1二叉排序树的节点类型

typedef struct BstNode//二叉树的节点类型
{
	KeyType key;	
	BstNode* parent;//父节点
	BstNode* leftchild;//左孩子
	BstNode* rightchild;//右孩子
}BstNode;

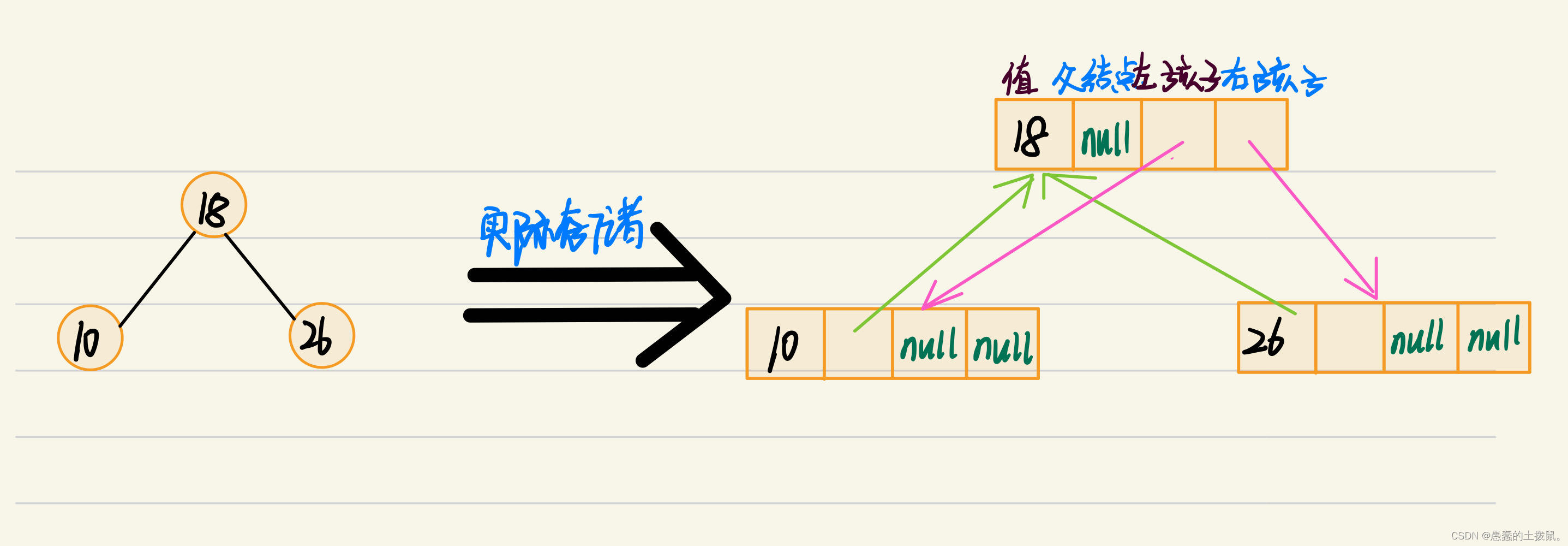
2.2二叉排序树中插入某个元素

bool Binary_Sort_Tree::Insert_Value(KeyType value)
{
//如果是一棵空树
	if (root ==nullptr)
	{
		root = MakeNode(value);//建立一个根节点
		return true;
	}

//如果不是一棵空树		
	BstNode* ptr = root;
	BstNode* parent = NULL;//记录ptr的父节点

	while (ptr != NULL && ptr->key != value)
	{
		parent = ptr;
		ptr = value > ptr->key ? ptr->rightchild : ptr->leftchild;
	}
//case1：插入相同元素
	if (ptr != NULL && ptr->key == value) return false;//不能插入相同元素
//case2：空位置
	ptr = MakeNode(value);
	ptr->parent = parent;

	if (ptr->key > parent->key) { parent->rightchild = ptr; }
	else { parent->leftchild = ptr; }
	cursize++;
	return true;
}

2.3 二叉排序树中按值查找元素

如果要查找的元素值>根节点值，就在根节点右边查找，否则在根节点左边查找。

BstNode* Binary_Sort_Tree::FindValue(KeyType value)
{
	BstNode* ptr = root;

	while (ptr != nullptr && ptr->key != value)
	{
		ptr = value > ptr->key ? ptr->rightchild : ptr->leftchild;
	}
	return ptr;
}

2.4 找排序二叉树中的最小值

根据排序二叉树的性质，可以很轻松的得到最小值即为最左边节点的值。

BstNode* Binary_Sort_Tree::FirstNodeByMiddleOrder()
{
	BstNode* ptr = root;
	while (ptr && ptr->leftchild)
	{
		ptr = ptr->leftchild;
	}
	return ptr;
}

2.5返回排序二叉树中ptr中序遍历的后续节点

节点ptr的后续节点为排序二叉树中第一个比ptr->key大的元素，即可以分为如下两种情况：
①如果ptr存在右子树，则ptr的后续节点为ptr右子树的最左端的节点。
②如果ptr不存在右子树，则ptr的后续节点可以回溯到根节点
具体如下：

BstNode* Binary_Sort_Tree::NextNodeByMiddleOrder(BstNode* ptr)
{			
	if (ptr == NULL) return ptr;
	if (ptr->rightchild != NULL)
	{
		return FirstNodeByMiddleOrder(ptr->rightchild);//右子树的最左端
	}
	else
	{
		BstNode* parent = ptr->parent;
		while (parent != NULL && parent->leftchild != ptr)//pa->rightleft == ptr;
		{
			ptr = parent;
			parent = ptr->parent;
		}
		return parent;
	}
}

2.6 寻找排序二叉树中的最大值

根据排序二叉树的性质，可以很轻松的得到最小值即为最右边节点的值。

BstNode* Binary_Sort_Tree::LastNodeByMiddleOrder()
{
	BstNode* ptr = root;
	while (ptr && ptr->rightchild)
	{
		ptr = ptr->rightchild;
	}
	return ptr;
}

2.7 寻找二叉树中中序遍历ptr节点的前驱

节点ptr的前驱为排序二叉树中第一个比ptr->key小的元素，即可以分为如下两种情况：
①如果ptr存在左子树，则ptr的后续节点为ptr左子树。
②如果ptr不存在左子树，则ptr的后续节点可以回溯到根节点
具体如下：

BstNode* Binary_Sort_Tree::PrecursorofPtr(BstNode* ptr)
{
	if (ptr == NULL) return ptr;
	if (ptr->leftchild != NULL)
	{
		return LastNodeByMiddleOrder(ptr->leftchild);//左子树的最右端
	}
	else
	{
		BstNode* parent = ptr->parent;
		while (parent != NULL && parent->rightchild != ptr)//pa->rightleft == ptr;
		{
			ptr = parent;
			parent = ptr->parent;
		}
		return parent;
	}
}

2.8中序遍历排序二叉树（从小到大打印排序二叉树所有元素）

void Binary_Sort_Tree::MiddleOrder()
{
	cout << "排序二叉树的非递归中序遍历：" << endl;
	BstNode* ptr = FirstNodeByMiddleOrder();
	for (; ptr != nullptr; ptr = NextNodeByMiddleOrder(ptr))
	{
		cout << ptr->key << "  ";
	}
	cout << endl;
}

2.9 逆向打印排序二叉树（从大到小打印排序二叉树所有元素）

void Binary_Sort_Tree::ReverseInorder()
{
	BstNode* ptr = root;
	cout << "二叉排序树的逆向打印：" << endl;
	for (BstNode* p = LastNodeByMiddleOrder(ptr); p != NULL; p = PrecursorofPtr(p))
	{
		cout << p->key << "  ";
	}
	cout << endl;
}

2.10删除排序二叉树的结点元素为value的结点

删除某个元素可分为以下三种情况：
①如果是叶子节点直接删除即可。
②如果不是叶子节点具体讨论如下：	

bool Binary_Sort_Tree::RemoveNode(KeyType value)
{
	BstNode* ptr = root;
	//空树的删除
	if (ptr == NULL) return false;

	BstNode* pa = NULL;
	BstNode* p = ptr;

	while (p && p->key != value)
	{
		//pa = p;
		p = value < p->key ? p->leftchild : p->rightchild;
	}
	//没有找到这个结点
	if (p == NULL) return false;

	//双分支
	if (p->leftchild && p->rightchild)
	{
		BstNode* q = FirstNodeByMiddleOrder(p->rightchild);
		p->key = q->key;
		p = q;
	}

	//单分支
	pa = p->parent;
	BstNode* child = p->leftchild != NULL ? p->leftchild : p->rightchild;
	if (child)
	{
		child->parent = pa;
	}
	if (pa == NULL)
	{
		ptr = child;
	}
	else
	{
		if (pa->leftchild == p)
		{
			pa->leftchild = child;
		}
		else
		{
			pa->rightchild = child;
		}
	}
	cursize--;
	//直接是叶子
	delete p;
	return true;
}

3.具体程序及运行结果

程序如下：
二叉排序树的代码下载