文章目录
- 4.1 感知机基本概念
- 4.2 策略
- 4.2.1 数据集的线性可分性
- 4.2.2 学习策略
- 目标
- 损失函数的构造
- 关于距离的解释
- 4.3 算法
- 4.3.1 原始形式
- 损失函数的梯度下降法
- 4.3.2 PLA例题
- 4.3.3 算法收敛性
- 4.4 PLA对偶形式
- 4.4.1 原始PLA分析
- 4.4.2 PLA对偶形式
- 4.4.3 优点
4.1 感知机基本概念
解决二分类问题,属于 线性分类模型——判别模型
目标:求出将训练数据进行线性划分的分离超平面
基本思想:导入五分类的损失函数,利用梯度下降法对损失i函数极小化,求得感知机模型
输入: x ∈ X ⊆ R n x\in \mathcal{X}\subseteq R^n x∈X⊆Rn 表示实例的特征向量, y ∈ Y = { + 1 , − 1 } y\in \mathcal{Y}=\{+1, -1\} y∈Y={+1,−1}
输出: ω ^ , b ^ \hat{\omega},\hat{b} ω^,b^
模型——决策函数
f
(
x
)
=
s
i
g
n
(
ω
T
x
+
b
)
=
{
+
1
,
ω
T
x
>
0
−
1
,
ω
T
x
<
0
f(x)=sign(\omega^Tx+b)=\begin{cases} +1&,\omega^Tx> 0\\ -1&,\omega^Tx<0 \end{cases}
f(x)=sign(ωTx+b)={+1−1,ωTx>0,ωTx<0
假设空间:定义在特征空间中的所有线性分类模型
{
f
∣
f
(
x
)
=
ω
T
x
+
b
}
\{f\vert f(x)=\omega^Tx+b\}
{f∣f(x)=ωTx+b}
几何理解:
ω
T
x
+
b
=
0
\omega^Tx+b=0
ωTx+b=0 在空间中为一个超平面
S
S
S ,
ω
\omega
ω 为法向量,
b
b
b 为截距
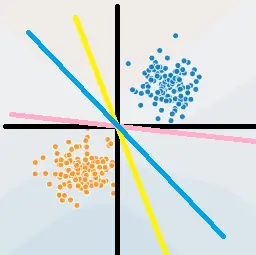
- 上图中超平面 S : ω 1 x ( 1 ) + ω 2 x ( 2 ) + b = 0 S:\omega_1x^{(1)}+\omega_2x^{(2)}+b=0 S:ω1x(1)+ω2x(2)+b=0 ,这个超平面将特征空间分为 + 1 , − 1 +1,-1 +1,−1 类
4.2 策略
损失函数的定义,并将 J ( ω ) J(\omega) J(ω) 最小化
4.2.1 数据集的线性可分性
对于数据集
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
x
i
∈
X
⊆
R
n
,
y
i
∈
Y
=
{
+
1
,
−
1
}
,
i
=
1
,
2
,
⋯
,
N
D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\\ x_i\in \mathcal{X}\subseteq R^n,y_i\in\mathcal{Y}=\{+1,-1\},i=1,2,\cdots,N
D={(x1,y1),(x2,y2),⋯,(xN,yN)}xi∈X⊆Rn,yi∈Y={+1,−1},i=1,2,⋯,N
若存在某个超平面
S
S
S :
ω
T
x
+
b
=
0
\omega^Tx+b=0
ωTx+b=0 ,将数据正负两类完全划分到超平面两侧
- 对于正例: y i = + 1 y_i=+1 yi=+1 ,有 ω T x + b > 0 \omega^Tx+b>0 ωTx+b>0
- 对于负例: y i = − 1 y_i=-1 yi=−1 ,有 ω T x + b < 0 \omega^Tx+b<0 ωTx+b<0
4.2.2 学习策略
目标
假设数据集D线性可分,找到将数据集D正负两例完全正确分开的超平面S,即确定参数 ω ^ , b ^ \hat{\omega},\hat{b} ω^,b^
损失函数的构造
可选择
- 误分类点的总数,但不关于 ω , b \omega,b ω,b 可导,是离散的
- 误分类点到超平面 S S S 的距离和
点
x
i
x_i
xi 到平面
S
S
S 的总距离
ω
T
x
i
+
b
∥
ω
∥
2
\frac{\omega^Tx_i+b}{\Vert \omega\Vert_2}
∥ω∥2ωTxi+b
对于误分类点有
y
i
⋅
(
ω
T
x
i
+
b
)
<
0
⟺
−
y
i
⋅
(
ω
T
x
i
+
b
)
>
0
y_i\cdot(\omega^Tx_i+b)<0\iff -y_i\cdot(\omega^Tx_i+b)>0
yi⋅(ωTxi+b)<0⟺−yi⋅(ωTxi+b)>0
对于误分类点,到超平面的几何距离为
−
1
∥
ω
∥
2
y
i
⋅
(
ω
T
x
i
+
b
)
-\frac{1}{\Vert \omega\Vert_2}y_i\cdot(\omega^Tx_i+b)
−∥ω∥21yi⋅(ωTxi+b)
若所有误分类点集合为
M
M
M ,则误分类点到
S
S
S 的距离和为
−
1
∥
ω
∥
2
∑
x
i
∈
M
y
i
⋅
(
ω
T
x
i
+
b
)
-\frac{1}{\Vert \omega\Vert_2}\sum\limits_{x_i\in M}y_i\cdot(\omega^Tx_i+b)
−∥ω∥21xi∈M∑yi⋅(ωTxi+b)
故将感知机(损失函数)定义为经验风险函数
R
e
m
p
(
f
)
=
L
(
ω
,
b
)
=
−
∑
x
i
∈
M
y
i
⋅
(
ω
T
x
i
+
b
)
R_{emp}(f)=L(\omega,b)=-\sum\limits_{x_i\in M}y_i\cdot(\omega^Tx_i+b)
Remp(f)=L(ω,b)=−xi∈M∑yi⋅(ωTxi+b)
策略为 在假设空间中选取使损失函数
L
(
ω
,
b
)
L(\omega,b)
L(ω,b) 最小的模型参数
ω
,
b
\omega,b
ω,b
- 损失函数非负
- 误分类点数量越少越好
- 误分类点离超平面越近越好
- L ( ω , b ) L(\omega,b) L(ω,b) 是连续可导的
关于距离的解释
− 1 ∥ ω ∥ 2 y i ⋅ ( ω T x i + b ) -\frac{1}{\Vert \omega\Vert_2}y_i\cdot(\omega^Tx_i+b) −∥ω∥21yi⋅(ωTxi+b) 为几何距离
− y i ⋅ ( ω T x i + b ) -y_i\cdot(\omega^Tx_i+b) −yi⋅(ωTxi+b) 为函数距离
几何距离的系数 1 ∥ ω ∥ 2 \frac{1}{\Vert \omega\Vert_2} ∥ω∥21 可以抵消系数同时放大的影响,如 a X + b Y + c = 0 aX+bY+c=0 aX+bY+c=0 与 2 a X + 2 b Y + 2 c = 0 2aX+2bY+2c=0 2aX+2bY+2c=0
- 但会增加梯度下降法计算的复杂度
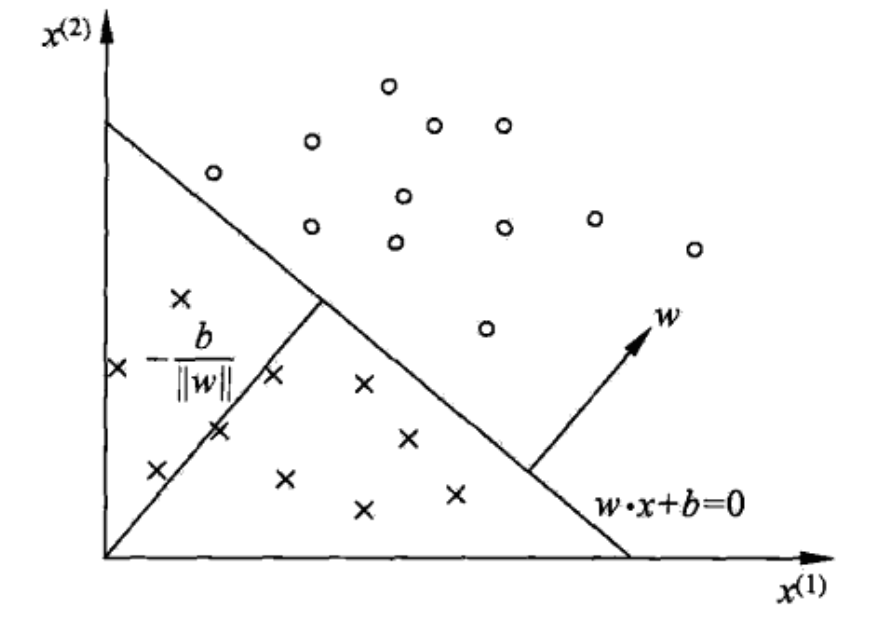
PLA的目标是使误分类点个数最小, 1 ∥ ω ∥ 2 \frac{1}{\Vert \omega\Vert_2} ∥ω∥21 对分类结果无影响
选取不同的初始 ω , b \omega,b ω,b ,最终会迭代出不同的超平面
4.3 算法
用随机梯度下降法,求解损失函数最优化问题
4.3.1 原始形式
输入:训练数据集
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
,
x
i
∈
X
⊆
R
n
,
y
i
∈
Y
=
{
+
1
,
−
1
}
,
i
=
1
,
2
,
⋯
,
N
D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\},\\ x_i\in \mathcal{X}\subseteq R^n,y_i\in \mathcal{Y}=\{+1,-1\},i=1,2,\cdots,N
D={(x1,y1),(x2,y2),⋯,(xN,yN)},xi∈X⊆Rn,yi∈Y={+1,−1},i=1,2,⋯,N
输出:
ω
^
,
b
^
\hat{\omega},\hat{b}
ω^,b^
模型
f
(
x
)
=
s
i
g
n
(
ω
T
x
+
b
)
=
{
+
1
,
ω
T
x
+
b
>
0
−
1
,
ω
T
x
+
b
<
0
f(x)=sign(\omega^Tx+b)=\begin{cases} +1&,\omega^Tx+b>0\\ -1&,\omega^Tx+b<0\\ \end{cases}
f(x)=sign(ωTx+b)={+1−1,ωTx+b>0,ωTx+b<0
策略
a
r
g
min
ω
,
b
L
(
ω
,
b
)
=
−
∑
x
i
∈
M
y
i
⋅
(
ω
T
x
i
+
b
)
arg\min\limits_{\omega,b}L(\omega,b)=-\sum\limits_{x_i\in M}y_i\cdot(\omega^Tx_i+b)
argω,bminL(ω,b)=−xi∈M∑yi⋅(ωTxi+b)
步骤
-
选取随机的 ω 0 , b 0 \omega_0,b_0 ω0,b0
-
在训练集中选数据 ( x i , y i ) (x_i,y_i) (xi,yi) ,将误分类点作为训练数据,即满足 ω T x i + b < 0 \omega^Tx_i+b<0 ωTxi+b<0 的条件的点
ω [ t + 1 ] ← ω [ t ] − η ∂ L ∂ ω = ω [ t ] + η y i x i b [ t + 1 ] ← b [ t ] − η ∂ L ∂ b = b [ t ] + η y i \omega^{[t+1]}\leftarrow\omega^{[t]}-\eta\frac{\partial L}{\partial \omega}=\omega^{[t]}+\eta y_ix_i\\ b^{[t+1]}\leftarrow b^{[t]}-\eta\frac{\partial L}{\partial b}=b^{[t]}+\eta y_i ω[t+1]←ω[t]−η∂ω∂L=ω[t]+ηyixib[t+1]←b[t]−η∂b∂L=b[t]+ηyi -
转至 2 2 2 步,直至 D D D 中无误分类点
损失函数的梯度下降法
{ ▽ ω L ( ω , b ) = − ∑ x i ∈ M y i x i ▽ b L ( ω , b ) = − ∑ x i ∈ M y i \begin{cases} \bigtriangledown_{\omega}L(\omega,b)=-\sum\limits_{x_i\in M}y_ix_i\\ \bigtriangledown_{b}L(\omega,b)=-\sum\limits_{x_i\in M}y_i\\ \end{cases} ⎩ ⎨ ⎧▽ωL(ω,b)=−xi∈M∑yixi▽bL(ω,b)=−xi∈M∑yi
前提是误分类点集合是固定的 ,才可进行梯度下降法最优化
{
ω
←
ω
−
η
▽
ω
L
b
←
b
−
η
▽
b
L
\begin{cases} \omega\leftarrow \omega-\eta\bigtriangledown_{\omega}L\\ b\leftarrow b-\eta\bigtriangledown_{b}L \end{cases}
{ω←ω−η▽ωLb←b−η▽bL
这种做法:
- 计算量大
- 且调整参数 ω , b \omega,b ω,b 后,误分类点集可能会发生变化,故用随机梯度下降法
直观理解
当一个样本点被误分类时,调整 ω , b \omega,b ω,b 的值,使超平面 S S S 向该误分类点的一侧移动,减少该误分类点与 S S S 的距离,直至超平面越过此点(分类正确)
4.3.2 PLA例题
x 1 = ( 3 , 3 ) T , y 1 = + 1 x 2 = ( 4 , 3 ) T , y 2 = + 1 x 3 = ( 1 , 1 ) T , y 3 = − 1 x_1=(3,3)^T,y_1=+1\\ x_2=(4,3)^T,y_2=+1\\ x_3=(1,1)^T,y_3=-1\\ x1=(3,3)T,y1=+1x2=(4,3)T,y2=+1x3=(1,1)T,y3=−1
模型:
f
(
x
)
=
s
i
g
n
(
ω
T
x
+
b
)
=
{
+
1
,
ω
T
x
+
b
>
0
−
1
,
ω
T
x
+
b
<
0
ω
=
(
ω
1
ω
2
)
f(x)=sign(\omega^Tx+b)=\begin{cases} +1&,\omega^Tx+b>0\\ -1&,\omega^Tx+b<0 \end{cases}\\ \omega=\left( \begin{aligned} \omega_1\\ \omega_2 \end{aligned} \right)
f(x)=sign(ωTx+b)={+1−1,ωTx+b>0,ωTx+b<0ω=(ω1ω2)
PLA策略为
min
ω
,
b
L
(
ω
,
b
)
=
−
∑
x
i
∈
M
y
i
(
ω
T
⋅
x
+
b
)
\min\limits_{\omega,b}L(\omega,b)=-\sum\limits_{x_i\in M}y_i(\omega^T\cdot x+b)
ω,bminL(ω,b)=−xi∈M∑yi(ωT⋅x+b)
算法:
-
取初值, ω 0 = ( 0 0 ) \omega_0=\left(\begin{aligned}0\\0\end{aligned}\right) ω0=(00) , b 0 = 0 b_0=0 b0=0 , η = 1 \eta=1 η=1
-
对 x 1 = ( 3 , 3 ) T x_1=(3,3)^T x1=(3,3)T ,有 y 1 ( ω 1 [ 0 ] x 1 ( 1 ) + ω 2 [ 0 ] x 1 ( 2 ) + b [ 0 ] ) = 0 y_1(\omega_1^{[0]}x_1^{(1)}+\omega_2^{[0]}x_1^{(2)}+b^{[0]})=0 y1(ω1[0]x1(1)+ω2[0]x1(2)+b[0])=0
未分类正确,故更新
{ ω [ 1 ] ← ω [ 0 ] − η ∂ L ∂ ω = ω [ 0 ] + η y i x i = ( 0 0 ) + ( 3 3 ) = ( 3 3 ) b [ 1 ] ← b [ 0 ] − η ∂ L ∂ b = b [ 0 ] + η y i = 0 + 1 ⋅ 1 = 1 \begin{cases} \omega^{[1]}\leftarrow\omega^{[0]}-\eta\frac{\partial L}{\partial \omega}=\omega^{[0]}+\eta y_ix_i= \left( \begin{aligned} 0\\0 \end{aligned} \right)+\left( \begin{aligned} 3\\3 \end{aligned} \right)=\left( \begin{aligned} 3\\3 \end{aligned} \right)\\ b^{[1]}\leftarrow b^{[0]}-\eta\frac{\partial L}{\partial b}=b^{[0]}+\eta y_i=0+1\cdot 1=1 \end{cases} ⎩ ⎨ ⎧ω[1]←ω[0]−η∂ω∂L=ω[0]+ηyixi=(00)+(33)=(33)b[1]←b[0]−η∂b∂L=b[0]+ηyi=0+1⋅1=1
故有线性模型
ω 1 T ⋅ x + b 1 = 3 x ( 1 ) + 3 x ( 2 ) + 1 \omega_1^{T}\cdot x+b_1=3x^{(1)}+3x^{(2)}+1 ω1T⋅x+b1=3x(1)+3x(2)+1 -
对 x 2 = ( 4 , 3 ) T , ( ω 1 [ 1 ] x 2 + ω 2 [ 1 ] x 2 + b [ 1 ] ) y 2 > 0 x_2=(4,3)^T,(\omega_1^{[1]}x_2+\omega_2^{[1]}x_2+b^{[1]})y_2>0 x2=(4,3)T,(ω1[1]x2+ω2[1]x2+b[1])y2>0 ,正确分类
x 3 = ( 1 , 1 ) T , ( ω 1 [ 1 ] x 3 + ω 2 [ 1 ] x 3 + b [ 1 ] ) y 3 < 0 x_3=(1,1)^T,(\omega_1^{[1]}x_3+\omega_2^{[1]}x_3+b^{[1]})y_3<0 x3=(1,1)T,(ω1[1]x3+ω2[1]x3+b[1])y3<0 ,误分类。用 ( x 3 , y 3 ) (x_3,y_3) (x3,y3) 更新模型参数
{ ω [ 2 ] ← ω [ 1 ] − η ∂ L ∂ ω = ω [ 1 ] + η y 3 x 3 = ( 3 3 ) + ( − 1 ) ( 1 1 ) = ( 2 2 ) b [ 1 ] ← b [ 0 ] − η ∂ L ∂ b = b [ 0 ] + η y 3 = 1 + 1 ⋅ ( − 1 ) = 0 \begin{cases} \omega^{[2]}\leftarrow\omega^{[1]}-\eta\frac{\partial L}{\partial \omega}=\omega^{[1]}+\eta y_3x_3= \left( \begin{aligned} 3\\3 \end{aligned} \right)+(-1)\left( \begin{aligned} 1\\1 \end{aligned} \right)=\left( \begin{aligned} 2\\2 \end{aligned} \right)\\ b^{[1]}\leftarrow b^{[0]}-\eta\frac{\partial L}{\partial b}=b^{[0]}+\eta y_3=1+1\cdot (-1)=0 \end{cases} ⎩ ⎨ ⎧ω[2]←ω[1]−η∂ω∂L=ω[1]+ηy3x3=(33)+(−1)(11)=(22)b[1]←b[0]−η∂b∂L=b[0]+ηy3=1+1⋅(−1)=0
有线性模型
ω 1 [ 2 ] x 1 + ω 2 [ 2 ] x 2 = 0 ⟺ 2 x 1 + 2 x 2 = 0 ⟺ x 1 + x 2 = 0 \omega^{[2]}_1x_1+\omega^{[2]}_2x_2=0\iff 2x_1+2x_2=0\iff x_1+x_2=0 ω1[2]x1+ω2[2]x2=0⟺2x1+2x2=0⟺x1+x2=0 -
对 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) (x_1,y_1),(x_2,y_2),(x_3,y_3) (x1,y1),(x2,y2),(x3,y3) 代入线性模型,反复迭代
直至无误分类样本点,有
ω
[
7
]
=
(
1
1
)
,
b
[
7
]
=
−
3
\omega^{[7]}=\left( \begin{aligned} 1\\1 \end{aligned} \right),b^{[7]}=-3
ω[7]=(11),b[7]=−3
超平面为
x
(
1
)
+
x
(
2
)
−
3
=
0
x^{(1)}+x^{(2)}-3=0
x(1)+x(2)−3=0
4.3.3 算法收敛性
对于线性可分的训练数据集,经过有限次迭代(PLA可以在有限步终止) ,可以得到一个将训练数据集完全正确划分的超平面 S S S
定理
训练集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\} D={(x1,y1),(x2,y2),⋯,(xN,yN)} ,对于二分类模型, x i ∈ X ⊆ R n x_i\in \mathcal{X}\subseteq R^n xi∈X⊆Rn , y i ∈ Y = { + 1 , − 1 } y_i\in \mathcal{Y}=\{+1,-1\} yi∈Y={+1,−1} , i = 1 , 2 , ⋯ , N ,i=1,2,\cdots,N ,i=1,2,⋯,N
-
一定存在 ∥ ω ^ ∗ ∥ = 1 \Vert \hat{\omega}_*\Vert=1 ∥ω^∗∥=1 的超平面 ω ^ ∗ x T = 0 \hat{\omega}_*x^T=0 ω^∗xT=0 ,将数据完全正确划分,且存在 γ > 0 \gamma >0 γ>0 ,使
y i ( ω ^ ∗ x T ) ≥ γ ω ^ = ( ω ∗ b ∗ ) , x = ( x 1 ) y_i(\hat{\omega}_*x^T)\ge \gamma\\ \hat{\omega}=\left(\begin{aligned} \omega_*\\ b_* \end{aligned} \right),x=\left( \begin{aligned} x\\1 \end{aligned} \right) yi(ω^∗xT)≥γω^=(ω∗b∗),x=(x1)
证:由于线性可分,则可找到一个超平面 S : ω ^ ∗ x T = 0 S:\hat{\omega}_*x^T=0 S:ω^∗xT=0 ,使所有数据 y i ( ω ^ ∗ x T ) > 0 y_i(\hat{\omega}_*x^T)>0 yi(ω^∗xT)>0 分类正确可取 γ = min i { y i ( ω ^ ∗ x T ) } \gamma=\min\limits_{i}\{y_i(\hat{\omega}_*x^T)\} γ=imin{yi(ω^∗xT)} ,距离超平面最近的点
-
令 R = max 1 ≤ i ≤ N ∥ x i ∥ 2 R=\max\limits_{1\le i\le N}\Vert x_i\Vert_2 R=1≤i≤Nmax∥xi∥2 ,样本特征值最大的二范数 ,则PLA在训练数据集上误分类次数 k k k 满足 K ≤ ( R γ ) 2 K\le \left(\frac{R}{\gamma}\right)^2 K≤(γR)2
即离超平面越近的点越难分
感知机存在许多解,依赖于初值的选择
- 即误分类点的选择次序会影响最终的结果
4.4 PLA对偶形式
4.4.1 原始PLA分析
在原始 PLA 算法中,
ω
0
,
b
0
=
0
\omega_0,b_0=0
ω0,b0=0 ,
L
(
ω
,
b
)
=
−
∑
x
i
∈
M
y
i
(
ω
T
⋅
x
+
b
)
L(\omega,b)=-\sum\limits_{x_i\in M}y_i(\omega^T\cdot x+b)
L(ω,b)=−xi∈M∑yi(ωT⋅x+b) ,采用随机梯度下降算法,取一个误分类点
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi) 作为学习数据,
η
∈
(
0
,
1
]
\eta\in(0,1]
η∈(0,1] 为学习率
{
ω
[
t
+
1
]
←
ω
[
t
]
−
η
∂
L
∂
ω
=
ω
[
t
]
+
η
y
i
x
i
b
[
t
+
1
]
←
b
[
t
]
−
η
∂
L
∂
b
=
b
[
t
]
+
η
y
i
\begin{cases} \omega^{[t+1]}\leftarrow\omega^{[t]}-\eta\frac{\partial L}{\partial \omega}=\omega^{[t]}+\eta y_ix_i\\ b^{[t+1]}\leftarrow b^{[t]}-\eta\frac{\partial L}{\partial b}=b^{[t]}+\eta y_i \end{cases}
{ω[t+1]←ω[t]−η∂ω∂L=ω[t]+ηyixib[t+1]←b[t]−η∂b∂L=b[t]+ηyi
可见
-
ω \omega ω 更新至于误分类点有关
某个点使用次数越多,距超平面越近,越难正确分类
-
假设 ( x i , y i ) (x_i,y_i) (xi,yi) 被误分类 n i n_i ni 次,则 ω \omega ω 在 ( x i , y i ) (x_i,y_i) (xi,yi) 上的累积量为
{ ω i ← n i η y i x i = α i y i x i b i ← n i η y i = α i y i \begin{cases} \omega_i\leftarrow n_i\eta y_ix_i=\alpha_iy_ix_i\\ b_i\leftarrow n_i\eta y_i=\alpha_iy_i \end{cases} {ωi←niηyixi=αiyixibi←niηyi=αiyi
且对于正确分类的点 n i = 0 n_i=0 ni=0 ,故原始PLA参数可表示为
{ ω ← ∑ j = 1 N n j η y j ⋅ x j b ← ∑ j = 1 N n j η y j \begin{cases} \omega\leftarrow \sum\limits_{j=1}^Nn_j\eta y_j\cdot x_j\\ b\leftarrow \sum\limits_{j=1}^N n_j\eta y_j \end{cases} ⎩ ⎨ ⎧ω←j=1∑Nnjηyj⋅xjb←j=1∑Nnjηyj
4.4.2 PLA对偶形式
输入: D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } , x i ∈ X ⊆ R n , y i ∈ Y = { + 1 , − 1 } , i = 1 , 2 , ⋯ , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\},x_i\in \mathcal{X}\subseteq R^n,y_i\in \mathcal{Y}=\{+1,-1\},i=1,2,\cdots,N D={(x1,y1),(x2,y2),⋯,(xN,yN)},xi∈X⊆Rn,yi∈Y={+1,−1},i=1,2,⋯,N
η ∈ ( 0 , 1 ] \eta\in (0,1] η∈(0,1]
模型
f
(
x
)
=
s
i
g
n
[
(
∑
j
=
1
N
n
j
η
y
j
⋅
x
j
)
T
⋅
x
+
∑
j
=
1
N
n
j
η
y
j
]
=
s
i
g
n
[
∑
j
=
1
N
α
j
y
j
(
x
j
⋅
x
)
T
+
b
]
\begin{aligned} f(x)&=sign[(\sum\limits_{j=1}^Nn_j\eta y_j\cdot x_j)^T\cdot x+\sum\limits_{j=1}^N n_j\eta y_j]\\ &=sign[\sum\limits_{j=1}^N\alpha_j y_j(x_j\cdot x)^T+b] \end{aligned}
f(x)=sign[(j=1∑Nnjηyj⋅xj)T⋅x+j=1∑Nnjηyj]=sign[j=1∑Nαjyj(xj⋅x)T+b]
输出 :
α
,
b
\alpha,b
α,b
α
=
(
α
1
α
2
⋮
α
N
)
\alpha=\left(\begin{aligned}\alpha_1\\\alpha_2\\\vdots\\\alpha_N\end{aligned}\right)
α=
α1α2⋮αN
,
α
i
=
n
i
η
\alpha_i=n_i\eta
αi=niη ,
n
i
n_i
ni 为
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi) 被误分类的次数
步骤
-
∀ n i = 0 \forall n_i=0 ∀ni=0 ,即 α = 0 , b = 0 \alpha=0,b=0 α=0,b=0
-
选取 ( x i , y i ) (x_i,y_i) (xi,yi) ,若 y i [ ∑ j = 1 N n j η y j ( x j T ⋅ x ) + ∑ j = 1 N n j η y j ] ≤ 0 y_i[\sum\limits_{j=1}^Nn_j\eta y_j(x_j^T\cdot x)+\sum\limits_{j=1}^N n_j\eta y_j]\le 0 yi[j=1∑Nnjηyj(xjT⋅x)+j=1∑Nnjηyj]≤0 ,则令
n [ t + 1 ] ← n [ t ] + 1 α [ t + 1 ] ← α [ t ] + η b [ t + 1 ] ← b [ t ] + η y i n^{[t+1]}\leftarrow n^{[t]}+1\\ \alpha^{[t+1]}\leftarrow \alpha^{[t]}+\eta\\ b^{[t+1]}\leftarrow b^{[t]}+\eta y_i n[t+1]←n[t]+1α[t+1]←α[t]+ηb[t+1]←b[t]+ηyi -
转至 2. 2. 2. 直至没有误分类点
由于样本点只以内积形式出现,可计算 Gram矩阵
G
=
[
x
i
⋅
x
j
]
N
×
N
=
[
(
x
1
,
x
1
)
(
x
1
,
x
2
)
⋯
(
x
1
,
x
N
)
(
x
2
,
x
1
)
(
x
2
,
x
2
)
⋯
(
x
2
,
x
N
)
⋮
⋮
⋱
⋮
(
x
N
,
x
1
)
(
x
N
,
x
2
)
⋯
(
x
N
,
x
N
)
]
G=[x_i\cdot x_j]_{N\times N}=\left[\begin{matrix} (x_1,x_1)&(x_1,x_2)&\cdots&(x_1,x_N)\\ (x_2,x_1)&(x_2,x_2)&\cdots&(x_2,x_N)\\ \vdots&\vdots&\ddots&\vdots\\ (x_N,x_1)&(x_N,x_2)&\cdots&(x_N,x_N) \end{matrix} \right]
G=[xi⋅xj]N×N=
(x1,x1)(x2,x1)⋮(xN,x1)(x1,x2)(x2,x2)⋮(xN,x2)⋯⋯⋱⋯(x1,xN)(x2,xN)⋮(xN,xN)
4.4.3 优点
可预先计算存储 Gram 矩阵,提高计算速度
可通过 Gram 矩阵引入核函数,有 K ( x , z ) = ϕ ( x ) ⋅ ϕ ( z ) K(x,z)=\phi(x)\cdot \phi(z) K(x,z)=ϕ(x)⋅ϕ(z) ,可解决非线性分类问题











![[kingbase运维之奇怪的现象]](https://img-blog.csdnimg.cn/e490cd4982e34efd9e8fbc17c56f0e22.jpeg#pic_center)