什么叫可达性
变量v的定义d:对变量v的赋值语句称为变量v的定义
变量v的使用:在某个表达式中引用变量v的值
当变量v被再次赋值时,上一次赋值对变量v的定义d就被kill掉了
如果定义d到点p之间存在一条路径,且在路径中定义d没有被kill掉,则称d可以到达p
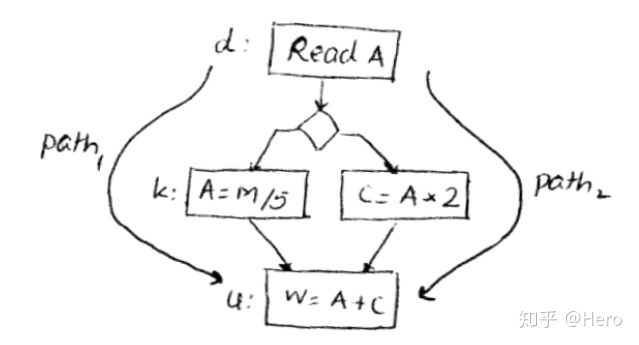
如下图所示,d可以通过path2到达u但是不能通过path1到达u,因为k这条语句kill掉了定义d。而因为d到u之间存在着没有被kill的路径path2,所以d可以到达u。
X = . 叫做精确定义,*p = . 叫做模糊定义,因为p可能指向X,一般考虑可达性只考虑精确定义对路径的kill。
数据依赖
两个句子存在数据依赖:一条语句中一个变量的定义,可以到达另一条语句中对该变量的使用
在编译领域有不同类型的数据依赖,如果我们说s2依赖于s1,可以是:
- s1 写内存 s2 读 (RAW)
- s1 读内存 s2 写 (WAR)
- s1 写内存 s2 写 (WAW)
- s1 读内存 s2 读 (RAR)
在软件工程领域,主要关注RAW依赖,在源码或IR的层度上。
DU-chains: def-use chains 优点是可以快速得到数据依赖,缺点是必须不断计算和更新,空间开销大。将每个语句作为结点,箭头作为有向边,即可得到数据依赖图。
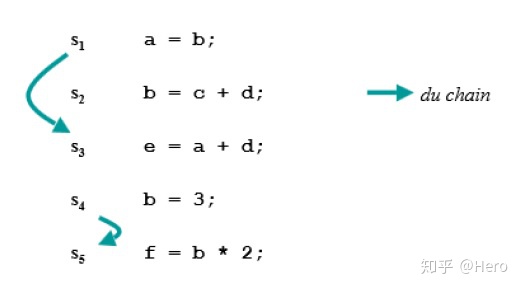
SSA:static single assignment 每一次赋值都由一个不同的变量表示,优点是使得分析变得简单高效,缺点是需要添加额外的条件才能正确执行,时空开销大。
如下图所示,转换为SSA就是使得每个变量只有一次定义。转换过程有两个步骤,分别为对每一个定义重命名,和对所有定义能到达的使用重命名。
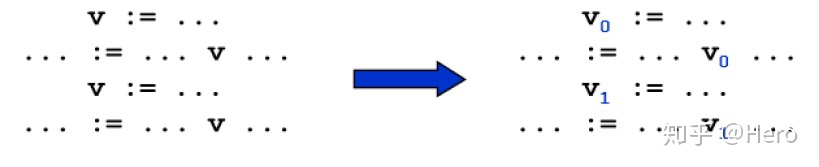
PDG:程序依赖图
程序依赖图的结点代表语句,边代表依赖关系,这里的依赖关系包括数据依赖和控制依赖
数据依赖:
s1: A = B * C;
s2: D = A * E + 1
由于s1语句变量A在s2语句中被读,因此称s2数据依赖于s1控制依赖:
s1: if (A) then
s2: B = C * D
endif
由于s1语句变量A的值决定了s2语句是否被执行,因此称s2控制依赖于s1其中控制依赖用实箭头表示,数据依赖用虚箭头表示。构建PDG图的整体流程如下。

首先做出其控制流图,从中找到控制依赖图和数据依赖图,结合起来即得到PDG图。数据依赖图上面已经说过了,控制依赖图由控制流图和FDT(Forward dominance Tree)产生。
FDT就是前向支配树,那么什么是支配树呢?编译原理里面有这样的一个概念,如果每一条从流图的入口结点到结点n的路径都经过结点d, 我们就说d支配(dominate)n,记为d dom n。请注意,在这个定义下每个结点都支配它自己。如下图所示,左侧为流图,右侧为其对应的支配树。

在支配树(dominator tree)中,对于结点n来说,从根节点到结点n所在路径上的结点都严格支配结点n,例如上图中从根节点1 -> 2 -> 3,其中结点1和结点2都严格支配结点3。该路径上离结点n最近的结点叫做结点n的直接支配结点(immediate node),用IDom(n)表示,例如上图中IDom(6) = 2。
前向支配树(FDT)指的就是根节点为函数出口的支配树,也就是上图的翻转,如下图所示,右侧为左侧函数对应的FDT(比如5->2的箭头表示,所有从函数出口到2的路径都一定会经过5,因此5是2的主导):
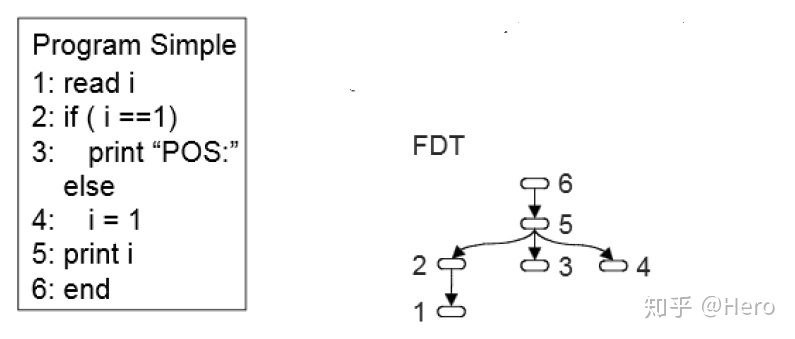
于是,得到FDT后将其与控制流图结合即可得到控制依赖图如下,有了控制依赖图,加上之前的数据依赖图,集合起来就得到了程序依赖图PDG。
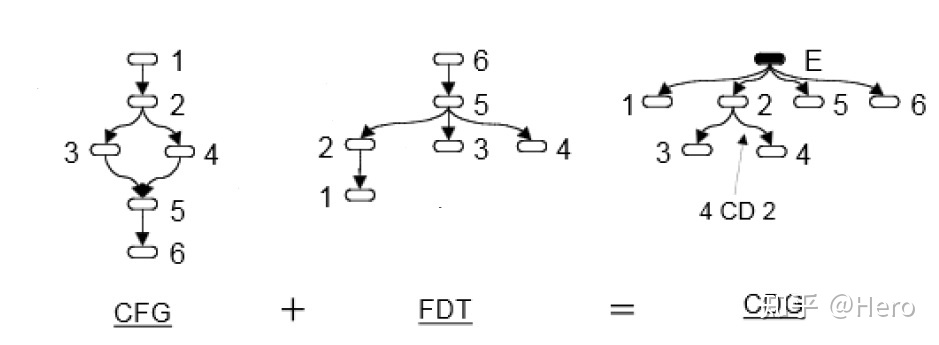
SDG:系统依赖图
系统依赖图,顾名思义,在PDG的基础上增加了一些点和边将整个系统整合在一起表示,对于系统中主函数的依赖图称为program dependence graph,对于其余函数称为procedure dependence graphs。
SDG中增加了5类新的结点:1)调用点 2)actual-in结点:它是具有与调用点相关的控制依赖,将实参的值传入一个临时单元中(例如x_in) 3) actual-out结点:也是具有与调用点相关的控制依赖,将临时单元中的值返回给实参 4)formal-in结点:它是具有与被调函数入口相关的控制依赖,将临时单元中的值复制给形参 5)formal-out结点:也是具有与被调函数入口相关的控制依赖,将形参中的值返回给临时单元
SDG中增加了3类新的边:1)从调用点指向被调函数入口结点的边 2)parameter-in边:actual-in结点指向formal-in结点的边(相当于实参->临时单元->形参) 3)parameter-out边: formal-out结点指向actual-out结点的边(相当于上述过程的返回过程)
一个SDG图的例子如下:

生成SDG的步骤:
1)首先先生成主函数的program dependence graph,和所有被调函数的procedure dependence graphs
2)对于每一个调用点,添加一条边指向被调函数的入口点
3)对于在调用点处的每一个actual-in的结点,添加一条parameter-in的边,指向被调函数对应的formal-in的结点
4)对于在调用点处的每一个actual-out的结点,添加一条parameter-out的边,由被调函数对应的formal-out的结点所指向
参考文献:
【1】Ferrante J, Ottenstein K J, Warren J D. The program dependence graph and its use in optimization[J]. ACM Transactions on Programming Languages and Systems (TOPLAS), 1987, 9(3): 319-349.
【2】Sinha S, Harrold M J, Rothermel G. System-dependence-graph-based slicing of programs with arbitrary interprocedural control flow[C]//Proceedings of the 1999 International Conference on Software Engineering (IEEE Cat. No. 99CB37002). IEEE, 1999: 432-441.
【3】Tip F. A survey of program slicing techniques[M]. Amsterdam: Centrum voor Wiskunde en Informatica, 1994.