CLEAN-SC 波束形成声源识别方法计算速度快、成像干净清晰、结果准确度高，但当传统延迟求和算法在各声源处输出的主瓣严重融合时，亦无法准确分辨声源。造成该缺陷的原因为: 主瓣严重融合时，CLEAN-SC 所基于的延迟求和输出峰值所在聚焦点即为声源点的假设不成立。从源相干性角度，若某聚焦点处的延迟求和输出主要由某声源贡献时，该聚焦点可标示该声源，即基于该聚焦点的位置及强度信息可重构该声源在各传声器处产生声压的互谱矩阵。鉴于此，以CLEAN-SC 识别的声源为初值迭代寻找正确的声源位置及强度，每次迭代中，最小化其余声源与某一声源的波束形成贡献的比值为每个声源选择标示点，根据标示点更新声源。仿真及试验均证明: 所给方法比传统CLEAN-SC 具有更高分辨率，使近距离低频率声源的准确识别变得可行。

基本理论

DAS

  图1 为波束形成声源识别的布局示意图，其利用一组传声器( 符号“◆”所示) 测量声压信号，假设聚焦声源面并离散为一组聚焦点( 符号“★”所示) ，基于DAS 进行后处理时，按聚焦点对各传声器测量的声压信号进行“相位对齐”和“求和运算”，使真实声源所在聚焦点的输出量被加强，其它聚焦点的输出量被衰减，从而识别声源。

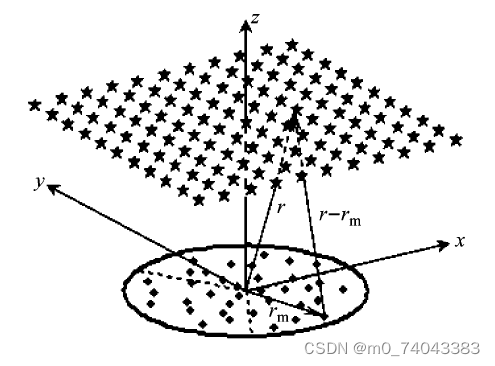
图1. 波束形成声源识别布局示意图
记$p$为各传声器测量的声压信号组成的列向量，$C=p{p}^H$为各传声器测量的声压信号的互谱矩阵，上标“H”表示转置共轭，$r$ 为聚焦点位置坐标，$\mu (r)$ 为$r$ 聚焦点的聚焦向量，则$r$ 聚焦点的DAS 输出$b(r)$ 为:
$$b(\mathbf{r})={\mathbf{\mu }}^H(\mathbf{r})\mathbf{C}\mathbf{\mu }(\mathbf{r})\text{\hspace{1em}(1)}$$
$$\mathbf{\mu }(\mathbf{r})=\frac{\mathbf{v}(\mathbf{r})}{||\mathbf{v}(\mathbf{r})|{|}_2^2}\text{\hspace{1em}(2)}$$
式中，$||\cdot |{|}_2$表示2范数，$\mathbf{v}(\mathbf{r})=[v_1(\mathbf{r}),v_2(\mathbf{r}),\cdots ,v_m(\mathbf{r}),\cdots ,v_M(\mathbf{r}){]}^T$为$r$聚焦点处声源的声波传播列向量，上标$T$ 表示转置， $m=1,2,\cdots ,M$为传声器索引， $M$为传声器总数，元素 $v_m(r)$表示 $r$聚焦点处的单位强度点声源在 $m$ 传声器处产生的声压，表达式为:
$$v_m(\mathbf{r})=\frac{exp(-jk|\mathbf{r}-{\mathbf{r}}_m|)}{\mathbf{r}-{\mathbf{r}}_m}\text{\hspace{1em}(3)}$$
式中 $j$ 为虚数单位，$k=2\pi f/c$为波数， $f$为频率， $c$ 为声速， $r_m$为m传声器的坐标位置。
  记${\mathbf{r}}_0$为声源位置坐标，$q({\mathbf{r}}_0)$为${\mathbf{r}}_0$处声源的强度，式(1)可写为：
$$\{\begin{array}{rl}b(\mathbf{r})& =\sum _{r_0}q({\mathbf{r}}_0)psf(\mathbf{r}|{\mathbf{r}}_0)\\ psf(\mathbf{r}|{\mathbf{r}}_0)& ={\mathbf{\mu }}^H(\mathbf{r})\mathbf{v}({\mathbf{r}}_0){\mathbf{v}}^H({\mathbf{r}}_0)\mathbf{\mu }(\mathbf{r})\end{array}\text{\hspace{1em}(4)}$$
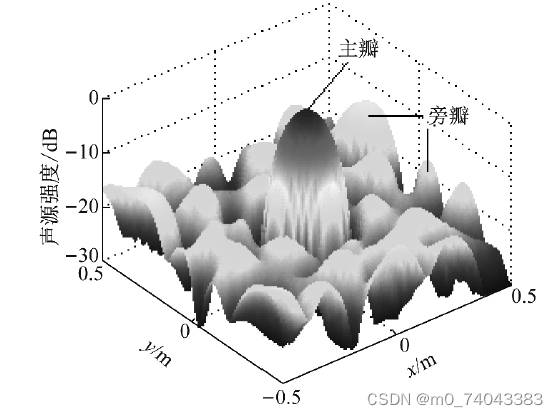
式中 $psf(\mathbf{r}|{\mathbf{r}}_0)$ 为 PSF，表示 ${\mathbf{r}}_0$处的单位强度点声源在r 聚焦点的DAS 贡献量，显然，$\mathbf{r}$ 聚焦点的DAS 输出等于各声源强度与对应PSF 的乘积的和。若PSF 等于理想的 $\delta$ 函数，DAS 将仅在声源所在聚焦点输出幅值等于声源强度的峰值，而在其它聚焦点输出0，声源识别准确。然而，实际应用中，传声器离散采样等因素使PSF 无法等于理想的$\delta$函数，图2 给出了聚焦声源面中心聚焦点处声源的PSF，其不仅在声源位置输出宽“主瓣”，还在非声源位置输出高“旁瓣”，主瓣宽度影响分辨率，旁瓣污染成像图，使识别结果的分析具有不确定性。因此，有必要对DAS 结果进行清晰化。

CLEAN-SC

  CLEAN-SC 是提高分辨率、衰减旁瓣的有效方法，其基于同一声源产生的主瓣与旁瓣相干的事实，通过反复在DAS 结果中移除与主瓣峰值指示的源相干的成分来清晰化声源识别结果。初始化传声器测量的声压信号的互谱矩阵$D^{(0)}=C$，声源强度分布$Q^{(0)}=0$，由第$n$ 次迭代到第$n+1$ 次迭代的步骤为:

1. 计算完成$n$次迭代后的 DAS 输出:
   $$b^{(n)}(\mathbf{r})={\mathbf{\mu }}^H(\mathbf{r}){\mathbf{D}}^{(n)}\mathbf{\mu }(\mathbf{r})$$
2. 搜索主瓣峰值：$b_{max}^{(n)}=max({\mathbf{b}}^{(n)})$，这里 ${\mathbf{b}}^{(n)}=[b^{(n)}(\mathbf{r})]$ 为所有聚焦点的DAS 输出组成的向量，并确定该峰值对应的聚焦点位置${\mathbf{r}}_{max}^{(n+1)}$；
3. 计算声源强度分布:
   $$Q^{(n+1)}({\mathbf{r}}_{max}^{(n+1)})=Q^{(n)}({\mathbf{r}}_{max}^{(n)})+b_{max}^{(n)}\text{\hspace{1em}(5)}$$
   其中，$Q(\cdot )$为矩阵 $Q$的元素，所在位置由括号内坐标向量指示。
4. 重构 $n+1$次迭代的互谱矩阵${\mathbf{D}}^{(n+1)}$ :
   $$\{\begin{array}{rl}{\mathbf{D}}^{(n+1)}& ={\mathbf{D}}^{(n)}-{\mathbf{G}}^{(n+1)}\\ {\mathbf{G}}^{(n+1)}& =b_{max}^{(n)}\mathbf{s}({\mathbf{r}}_{max}^{(n+1)}){\mathbf{s}}^H({\mathbf{r}}_{max}^{(n+1)})\end{array}\text{\hspace{1em}(6)}$$
   式中，${\mathbf{G}}^{(n+1)}$为分析主瓣峰值与其它聚焦点DAS 输出间的相干性而获得的互谱矩阵，$\mathbf{s}({\mathbf{r}}_{max}^{(n+1)})$为相应的源成分向量。对于任意$\mathbf{r}$ 聚焦点， ${\mathbf{G}}^{(n+1)}$满足${\mathbf{\mu }}^H(\mathbf{r}){\mathbf{D}}^{(n)}\mathbf{\mu }({\mathbf{r}}_{\mathbf{max}}^{(\mathbf{n}+1)})={\mathbf{\mu }}^H(\mathbf{r}){\mathbf{G}}^{(n+1)}\mathbf{\mu }({\mathbf{r}}_{max}^{(n+1)})$，即，${\mathbf{D}}^{(n)}\mathbf{\mu }({\mathbf{r}}_{\mathbf{max}}^{(\mathbf{n}+1)})={\mathbf{G}}^{(n+1)}\mathbf{\mu }({\mathbf{r}}_{max}^{(n+1)})$成立，该式与式（6）联立得：
   $$\mathbf{s}({\mathbf{r}}_{max}^{(n+1)})=\frac{{\mathbf{D}}^{(n)}\mathbf{\mu }({\mathbf{r}}_{\mathbf{max}}^{(\mathbf{n}+1)})}{b_{max}^{(n)}}\text{\hspace{1em}(7)}$$
   重构出${\mathbf{D}}^{(n+1)}$ 后，返回第1 步重复循环，直至完成规定的迭代数$N_1$，${\mathbf{Q}}^{(N_1)}$ 便是最终声源强度分布$\mathbf{Q}$。

HR-CLEAN-SC

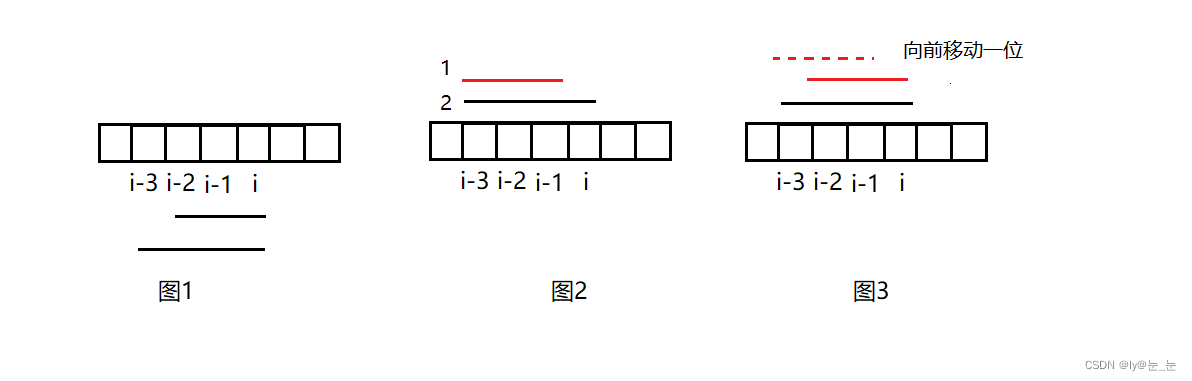
  称重构声源在各传声器处产生声压信号的互谱矩阵 $\mathbf{G}$ 时所基于的聚焦点为声源标示点，声源标示点所指示的声源为标示声源。传统CLEAN-SC采用的声源标示点为DAS 输出峰值所在的聚焦点，其指示的声源位于峰值位置，强度等于峰值。当DAS输出的主瓣轻微融合或未融合时，峰值中标示声源的贡献成分远大于其它声源，互谱矩阵重构准确，
CLEAN-SC 的声源识别正确; 当DAS 输出的主瓣严重融合时，峰值中各声源的贡献成分均较大，CLEAN-SC将无法正确识别声源。事实上，只要DAS 在声源标示点处的输出主要由标示声源贡献时，便可基于标示点
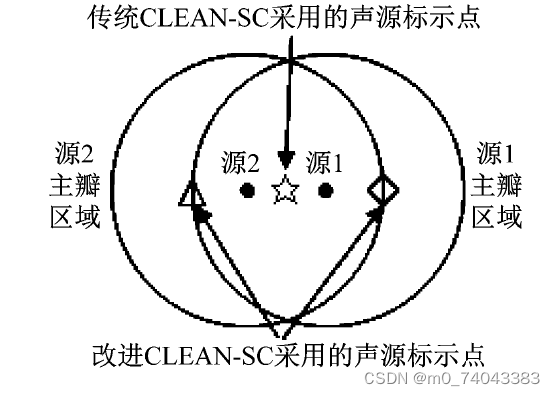
准确重构标示声源在各传声器处产生声压信号的互谱矩阵，进而准确识别声源。基于该事实，通过重新选择声源标示点重新确定标示声源来提高DAS 输出的主瓣严重融合时的声源识别准确度。图3 为声源标示点的选择示意图，“·”表示声源，DAS 在各声源处输出的主瓣落在以各声源为圆心的圆内，符号“☆”为传统CLEAN-SC 采用的声源标示点( 峰值点) ，符号“◇”和“△”为改进CLEAN-SC 分别为源1 和2 重新选择的标示点，源1 的标示点( ◇) 落在源1 的主瓣内、源2 的主瓣边界上，源1 在该位置的贡献显著大于源2，源2 的标示点( △) 落在源2 的主瓣内、源1 的主瓣边界上，源2 在该位置的贡献显著大于源1。

   改进CLEAN-SC（HR-CLEAN-SC） 的具体流程如下。首先，根据传统 CLEAN-SC 重构的声源强度分布$\mathbf{Q}$确定声源总数$I$、初始化声源位置$r_{0i}^{(0)}$和声源强度 ${\mathbf{Q}}^{(0)}(r_{0i}^{(0)})$，其中， $i=1,2,\cdots ,I$为声源索引，${\mathbf{Q}}^{(0)}(r_{01}^{(0)})>{\mathbf{Q}}^{(0)}(r_{02}^{(0)})>\cdots >{\mathbf{Q}}^{(0)}(r_{0I}^{(0)})$。然后，迭代寻找正确的声源位置和声源强度，每次迭代包含声源标示点确定、声源位置及强度确定、源排序三步，由第$n$次迭代到第n + 1 次迭代的步骤为:
   步骤1 依次确定每个声源的标示点：
$${\mathbf{r}}_{mai}^{(n+1)}={\mathbf{r}}_{ma}^{(n+1)}({\mathbf{r}}_{0i}^{(n)})=ar{g}_r\min F({\mathbf{r}}_{0i}^{(n)},\mathbf{r})$$
式中 ${\mathbf{r}}_{mai}^{(n+1)}={\mathbf{r}}_{ma}^{(n+1)}({\mathbf{r}}_{0i}^{(n)})$为第 $n$次迭代确定的第 $i$ 号声源的标示点，$F({\mathbf{r}}_{0i}^{(n)},\mathbf{r})$为成本函数，表达式为：
$$F({\mathbf{r}}_{0i}^{(n)},\mathbf{r})=\{\begin{array}{rlr}\frac{||{\sum }_{k=1,k\ne i}^l{\mathbf{v}}^H({\mathbf{r}}_{0k}^{(n)})\mathbf{\mu }(\mathbf{r})\mathbf{v}({\mathbf{r}}_{0k}^{(n)})|{|}_2^2}{|{\mathbf{v}}^H({\mathbf{r}}_{0i}^{(n)})\mathbf{\mu }(\mathbf{r}){|}^2||\mathbf{v}({\mathbf{r}}_{0i}^{(n)})|{|}_2^2},& & |{\mathbf{v}}^H({\mathbf{r}}_{0i}^{(n)})\mathbf{\mu }(\mathbf{r}){|}^2\ge 0.25\\ +\infty ,& & |{\mathbf{v}}^H({\mathbf{r}}_{0i}^{(n)})\mathbf{\mu }(\mathbf{r}){|}^2<0.25\end{array}\text{\hspace{1em}(9)}$$
式中 $k$ 为声源索引，$|{\mathbf{v}}^H({\mathbf{r}}_{0i}^{(n)})\mathbf{\mu }(\mathbf{r}){|}^2<0.25$ 时， $F({\mathbf{r}}_{0i}^{(n)},\mathbf{r})=+\infty$ 是为了保证DAS 在确定的声源标示点位置的输出比DAS 在声源位置的输出小不超过6dB，即确定的声源标示点落在主瓣内，$|{\mathbf{v}}^H({\mathbf{r}}_{0i}^{(n)})\mathbf{\mu }(\mathbf{r}){|}^2\ge 0.25$ 时，$F({\mathbf{r}}_{0i}^{(n)},\mathbf{r})$的表达式可理解为 $I$ 个单位强度声源中，除i 号声源外的其它声源在$\mathbf{r}$聚焦点处的波束形成贡献与$i$号声源在$\mathbf{r}$聚焦点处的波束形成贡献的比值。

   步骤2 基于确定的声源标示点，确定新的声源位置和声源强度。采用与传统CLEAN-SC 类同的相干性分析得声源标示点${\mathbf{r}}_{mai}^{(n+1)}$所标示的声源在各传声器处产生声压信号的互谱矩阵为:
$${\mathbf{G}}_i^{(n+1)}=\lambda ({\mathbf{r}}_{mai}^{(n+1)})\mathbf{s}({\mathbf{r}}_{mai}^{(n+1)}){\mathbf{s}}^H({\mathbf{r}}_{mai}^{(n+1)})\text{\hspace{1em}(10)}$$
$$\lambda ({\mathbf{r}}_{mai}^{(n+1)})={\mathbf{\mu }}^H({\mathbf{r}}_{mai}^{(n+1)})(\mathbf{C}-\sum _{k=1}^{i-1}{\mathbf{G}}_k^{(n+1)})\mathbf{\mu }({\mathbf{r}}_{mai}^{(n+1)})\text{\hspace{1em}(11)}$$
$$\mathbf{s}({\mathbf{r}}_{mai}^{(n+1)})=\frac{(\mathbf{C}-{\sum }_{k=1}^{i-1}{\mathbf{G}}_k^{(n+1)})\mathbf{\mu }({\mathbf{r}}_{mai}^{(n+1)})}{\lambda ({\mathbf{r}}_{mai}^{(n+1)})}\text{\hspace{1em}(12)}$$
式中，$\lambda ({\mathbf{r}}_{mai}^{(n+1)})$ 和 $\mathbf{s}({\mathbf{r}}_{mai}^{(n+1)})$分别为标示声源的成分系数和成分向量。计算 DAS 输出 $b_i^{(n+1)}(\mathbf{r})={\mathbf{\mu }}^H(\mathbf{r})\times {\mathbf{G}}_i^{(n+1)}\mathbf{\mu }(\mathbf{r})$，搜索主瓣峰值所在位置得新的声源位置 ${\mathbf{r}}_{0i}^{(n+1)}$，，主瓣峰值为相应声源强度${\mathbf{Q}}^{(n+1)}({\mathbf{r}}_{0i}^{(n+1)})$.对 $i=1,2,\cdots ,I$，依次进行上述分析。

   步骤3 对第2 步获得的$I$个声源按声源强度降序排列，返回第1 步重复循环，直至完成规定的迭代次数$N_2$。最后，获得声源强度分布$\mathbf{Q}$
$$\mathbf{Q}(\mathbf{r})=\{\begin{array}{rlr}{\mathbf{Q}}^{(N_2)}({\mathbf{r}}_{0i}^{(N_2)}),& & \mathbf{r}={\mathbf{r}}_{0i}^{(N_2)}\\ 0,& & \mathbf{r}\ne {\mathbf{r}}_{0i}^{(N_2)}\end{array}\text{\hspace{1em}(13)}$$

CLEAN-SC-CG

   为了减少CLEAN - SC 的计算时间及提升CLEAN-SC 的空间分辨率，提出了CLEAN-SC-CG算法。CLEAN-SC-CG 算法利用 FB 算法对声源进行初始定位，将获得初始定位结果作为CLEAN-SC 的初始值，然后通过设置阈值对初始值进行筛选，大于阈值的初始值及其相对应的网格信息被保留下来，其他初始值则不参与迭代运算，并另赋它值。
   FB 算法是在CBF 算法的基础上将CSM 进行特征值分解
$$\mathbf{C}=\mathbf{U}\Sigma {\mathbf{U}}^{\ast }\text{\hspace{1em}(14)}$$
式中，$\mathbf{U}$为酉矩阵，$\mathbf{U}=（u_1,\cdots ,u_N）$， $u_1,\cdots ,u_N$为 $\mathbf{C}$的特征向量；$\Sigma$为对角矩阵，$\Sigma =diag({\alpha }_1,\cdots ,{\alpha }_N)$，其中，${\alpha }_1,\cdots ,{\alpha }_N$为 $\mathbf{C}$的特征值。
FB算法的计算表达式
$$A_v(\xi )=[{\mathbf{w}}^{\ast }{\mathbf{C}}^{\frac{1}{v}}\mathbf{w}{]}^v=[{\mathbf{w}}^{\ast }\mathbf{U}{\Sigma }^{\frac{1}{v}}{\mathbf{U}}^{\ast }\mathbf{w}{]}^v\text{\hspace{1em}(15)}$$
式中，$\nu$ 为一个需要根据具体数据集确定的指数。与CBF 相比，FB 算法通过指数 $\nu$ 衰减与旁瓣相关的PSF值，达到抑制旁瓣、提升空间分辨率的目的，本文指数$\nu$取值为16。
在CLEAN-SC-CG 中，仅保留满足下式的聚焦网格点
$$A_v(\xi )>{\beta }_v\text{\hspace{1em}(16)}$$
式中，${\beta }_v$为阈值。阈值并非一个确定值，本文依据两个原则确定阈值的取值范围。原则一为背景噪声，一般低于背景噪声的声源不被关注，试验环境中背景噪声的声压级可以作为阈值的最小值; 原则二为声压级低于峰值 20 dB 的噪声，低于峰值20 dB 的噪声源对声场中目标声源的识别影响较小，所以，此噪声源的声压级可以作为阈值的最大值。阈值影响CLEAN-SC-CG压缩聚焦网格点的数量以及声像图中旁瓣的干扰程度，可根据试验环境和试验目的确定阈值的取值。

   步骤1：由式 (15) 计算函数波束形成输出$A_v(\xi )$
   步骤2：根据式$A_v(\xi )>{\beta }_v$，压缩聚焦网格点；
   步骤3：保留符合筛选条件的 ${\tilde{A}}_v(\xi )$及相应的网格点位置信息${\tilde{A}}_v(\xi )=A^{(0)}$，否则$A_v(\xi )=\alpha ，(\alpha <<{\beta }_v)$。
   步骤4： 对满足条件的网格点信息进行反卷积( CLEAN-SC) 计算，得出“干净”声像图。

MATLAB 仿真

matlab代码实现见CLEAN-SC

CLEAN_SC.m: 完成CLEAN-SC算法，并画出CLEAN-SC仿真定位图，并输出完成主体算法的运行时间

CLEAN_SC_CG.m：完成CLEAN-SC-CG算法，且画出CLEAN-SC-CG仿真定位图，以及加入CG算法之后的压缩比，和输出完成主体算法的运行时间

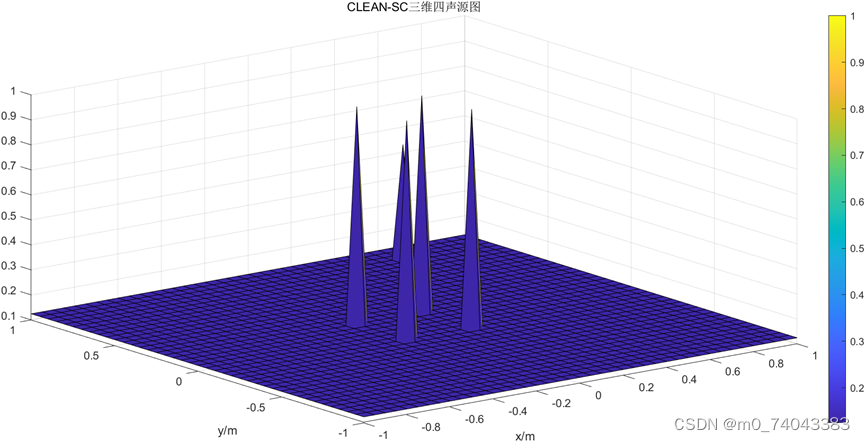
HR_CLEAN_SC.m ： 完成HR-CLEAN-SC算法，且画出CLEAN-SC 和HR-CLEAN-SC的仿真定位图对比，HR_CLEAN_SC三维图，并输出完成主体算法的运行时间

HR_CLEAN_SC_CG.m：完成HR-CLEAN-SC-CG算法，且画出CLEAN-SC-CG 和HR-CLEAN-SC-CG的仿真定位图对比，HR_CLEAN_SC_CG。以及加入CG之后的压缩比和运行时间

CLEAN_SC_1.m ：完成CLEAN-SC算法，并参照王月论文的输出声源强度分布图。

CLEAN_SC_CG_1.m：完成 CLEAN-SC-CG，完成CLEAN-SC-CG算法，输出CBF三维四声源强度分布图、BF三维四声源强度分布图、CLEAN-SC-CG三维四声源强度分布图。

HR-CLEAN-SC 定位准确性提升比较

① f = 1000 时

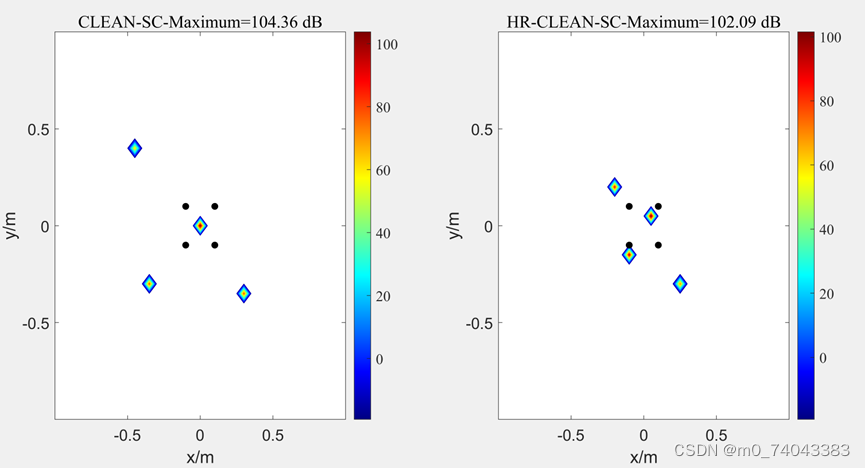
② f = 2000
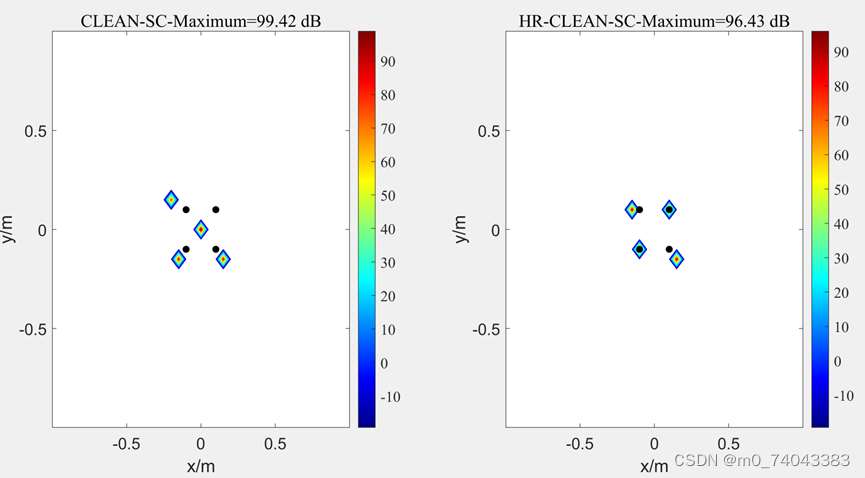③ f = 3000

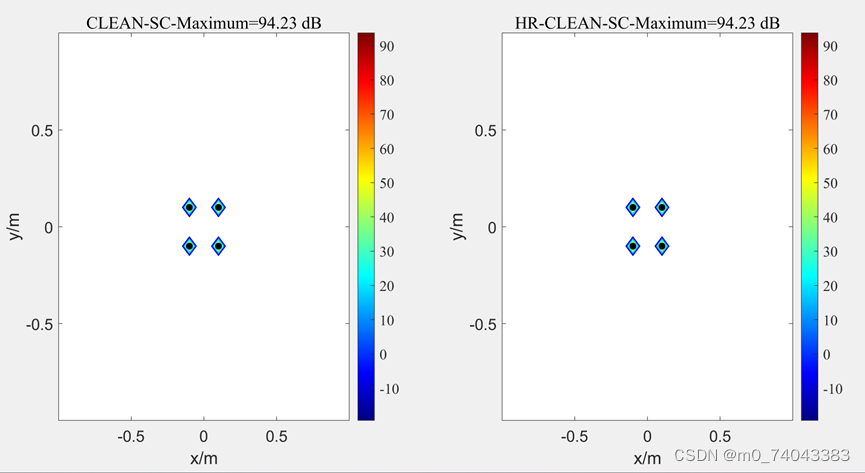
CG算法的压缩率

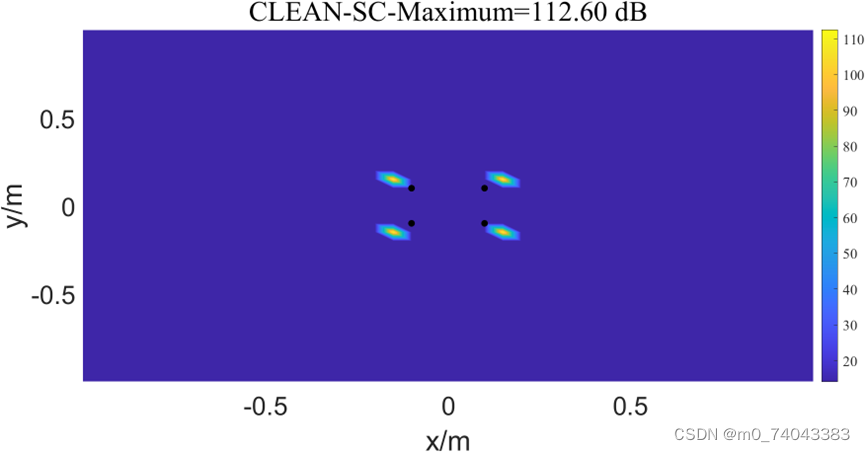
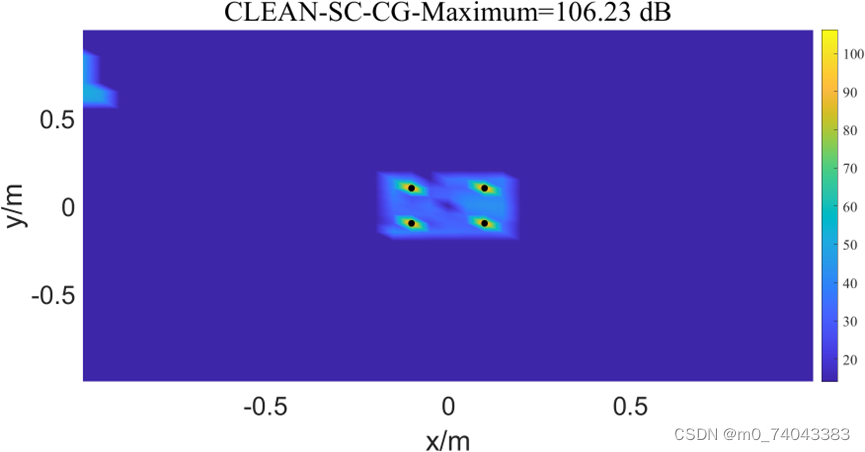
四声源的PSF图

① CBF 三维图

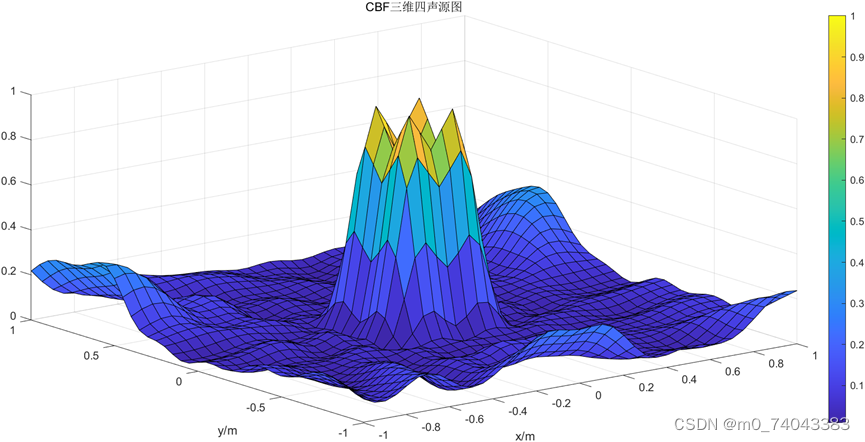
② BF 三维图

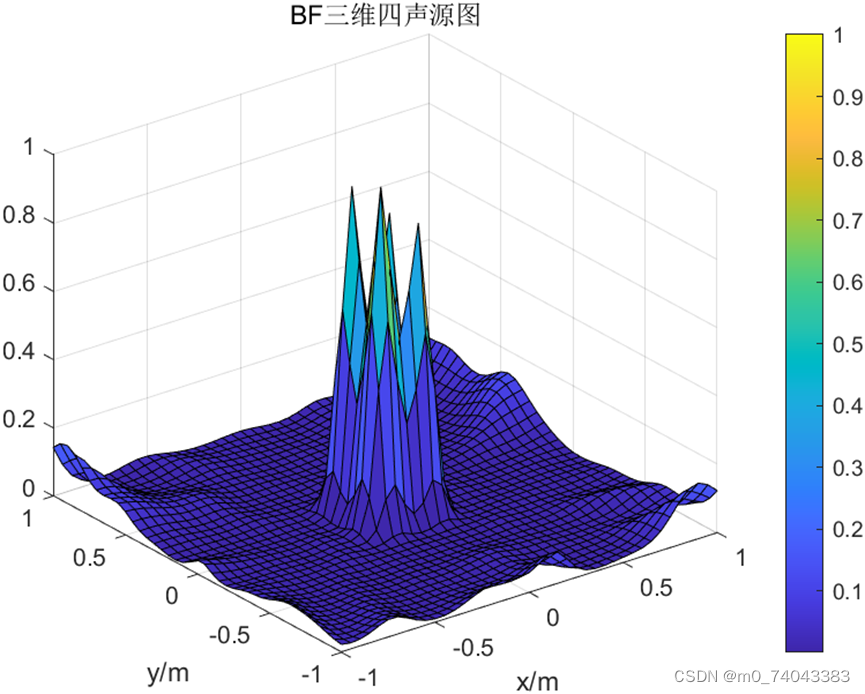
③ CLEAN-SC-CG 三维图

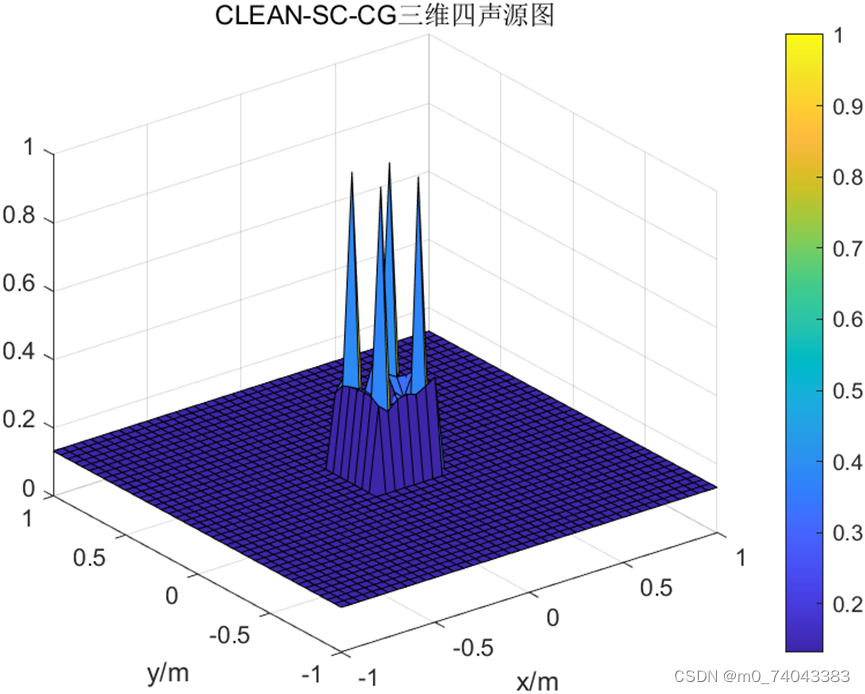
④ CLEAN-SC三维图