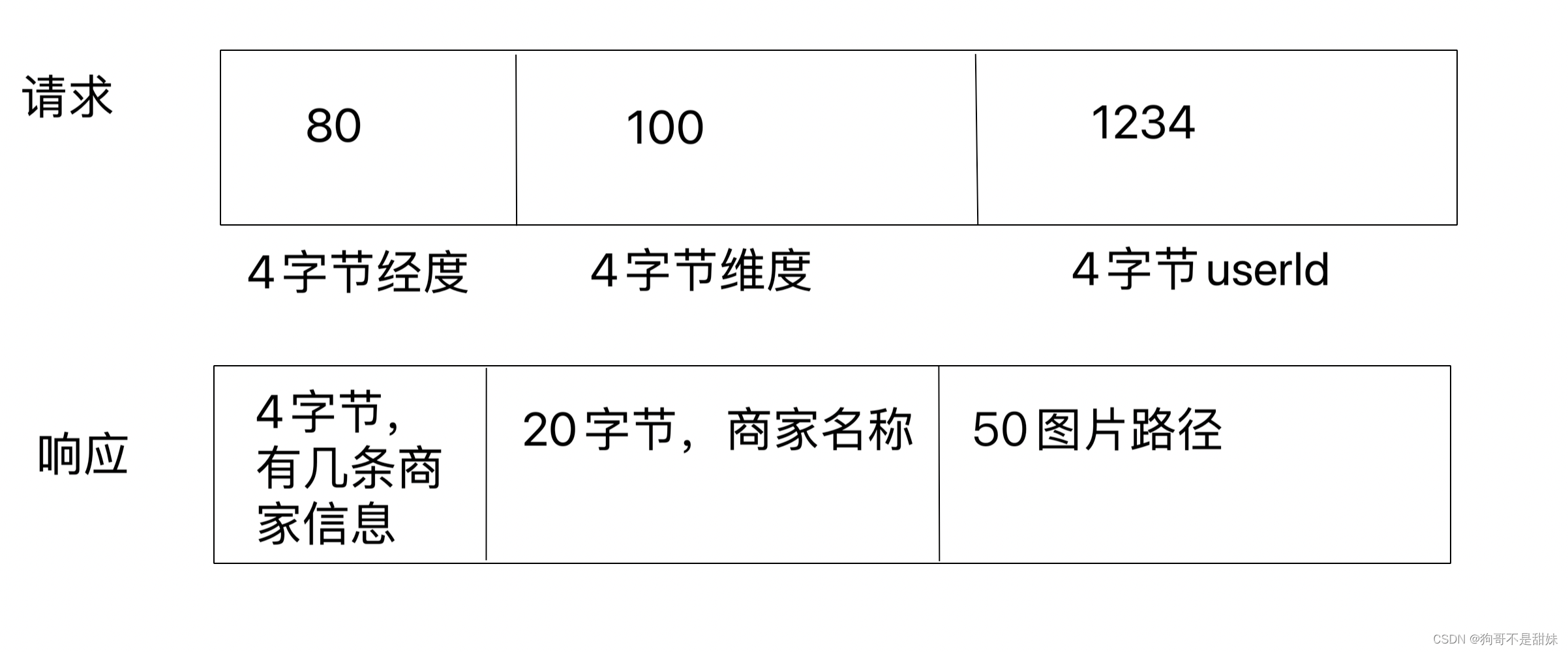
AVL树是最早发明的自平衡二叉查找树。在AVL树中,任一节点对应的两颗子树的最大高度差为1,因此他被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 O ( log n ) O(\log{n}) O(logn)增加和删除操作后可能需要通过一次货多次旋转来实现平衡
AVL树结构
- 可以是空树
- 任一节点对应的两颗子树的最大高度差为1
下面的两颗树就不是AVL树
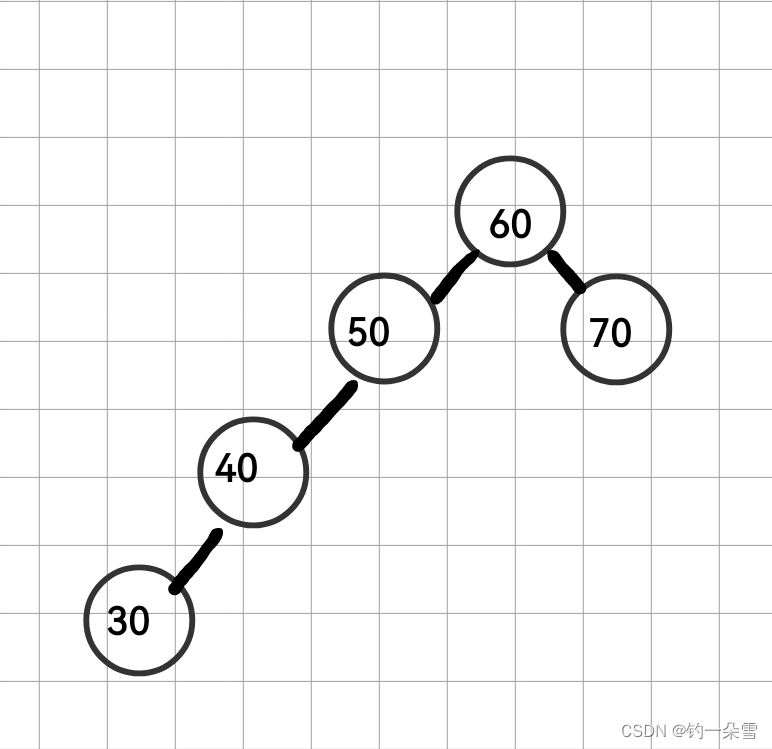
50节点的左子树高度为2右子树的高度为0;60节点左子树高度为3左子树高度为1,不满足条件。
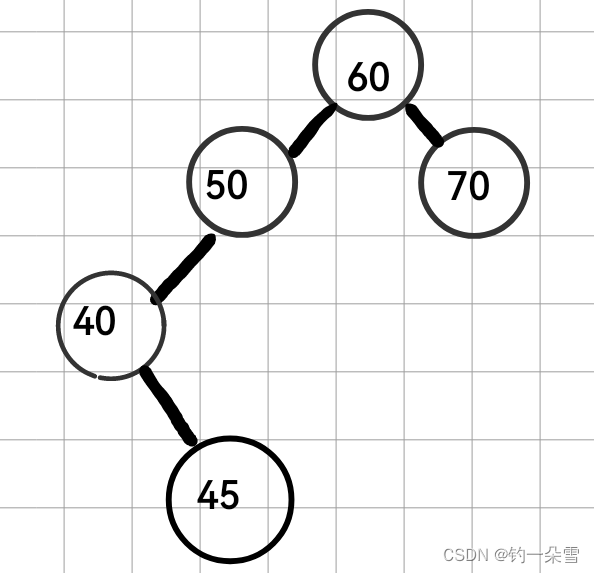
50节点的左子树高度为2右子树的高度为0;60节点左子树高度为3左子树高度为1,不满足条件。
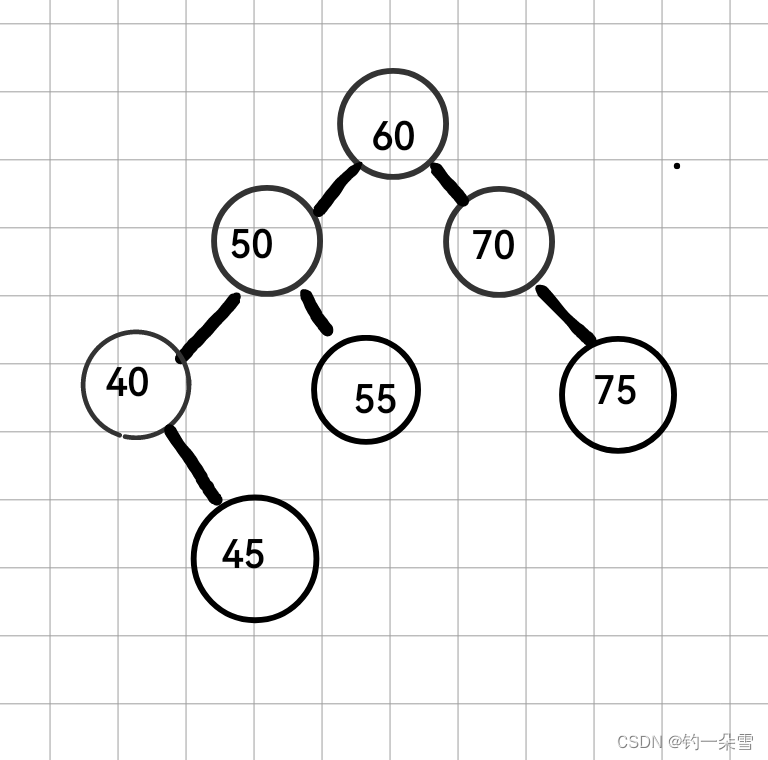
下面这棵树是AVL树
节点结构
typedef struct AVL
{
int data;
int bf; //平衡因子
struct AVL* left;
struct AVL* right;
struct AVL* parent;
}AVL;
平衡因子为右子树和左子树的高度差
| 平衡因子取值 | 含义 |
|---|---|
| 0 | 左子树和右子树一样高 |
| 1 | 右子树比左子树高1 |
| -1 | 左子树比右子树高1 |
| 2 | 不平衡了,需要通过旋转平衡 |
| -2 | 不平衡了,需要通过旋转平衡 |
AVL树的插入
AVL树插入节点的步骤
- 按照二叉搜索树的插入方法找到待插入节点
- 找到待插入节点后,将节点插入树中。
- 更新平衡因子,判断是否需要继续更新/旋转
- 如果需要旋转,判断旋转类型
更新平衡因子的规则
- 如果插入节点是parent的左孩子,则parent的平衡因子–
- 如果插入节点是parent的右孩子,则parent的平衡因子++
更新完一个节点的平衡因子后的判断
- 如果parent平衡因子为1或-1,则要继续往上更新
- 如果parent的平衡因子为0,则无需继续往上更新平衡因子
- 如果parent的平衡因子为2或-2,则表明以parent为根的子树已经不平衡,需要进行旋转。
解释 - 因为只有parent的平衡因子为0时经过++或者–操作才会变成1/-1,这说明插入后parent的左子树或者右子树变高了,那么以parent为根的子树变高了,从而影
响了parent的父节点的平衡因子,所以要往上更新。 - 因为只有parent的平衡因子为-1/1时经过++或者–操作才会变成0,说明插入前parent左右子树高度不一,新节点插入到了较矮的子树上,那么插入后并没有影响以parent为根的树的高度,从而不会影响parent的父节点的平衡因子。
判断旋转类型
向上更新的过程中必然指向下面的逻辑
cur=parent;
parent=parent->_parent;
那么根据cur的平衡因子和parent的平衡因子就可以判断旋转类型
| parent->bf | cur->bf | 旋转类型 |
|---|---|---|
| 2 | 1 | 左单旋 |
| 2 | -1 | 右左双旋 |
| -2 | 1 | 左右双旋 |
| -2 | -1 | 右单旋 |
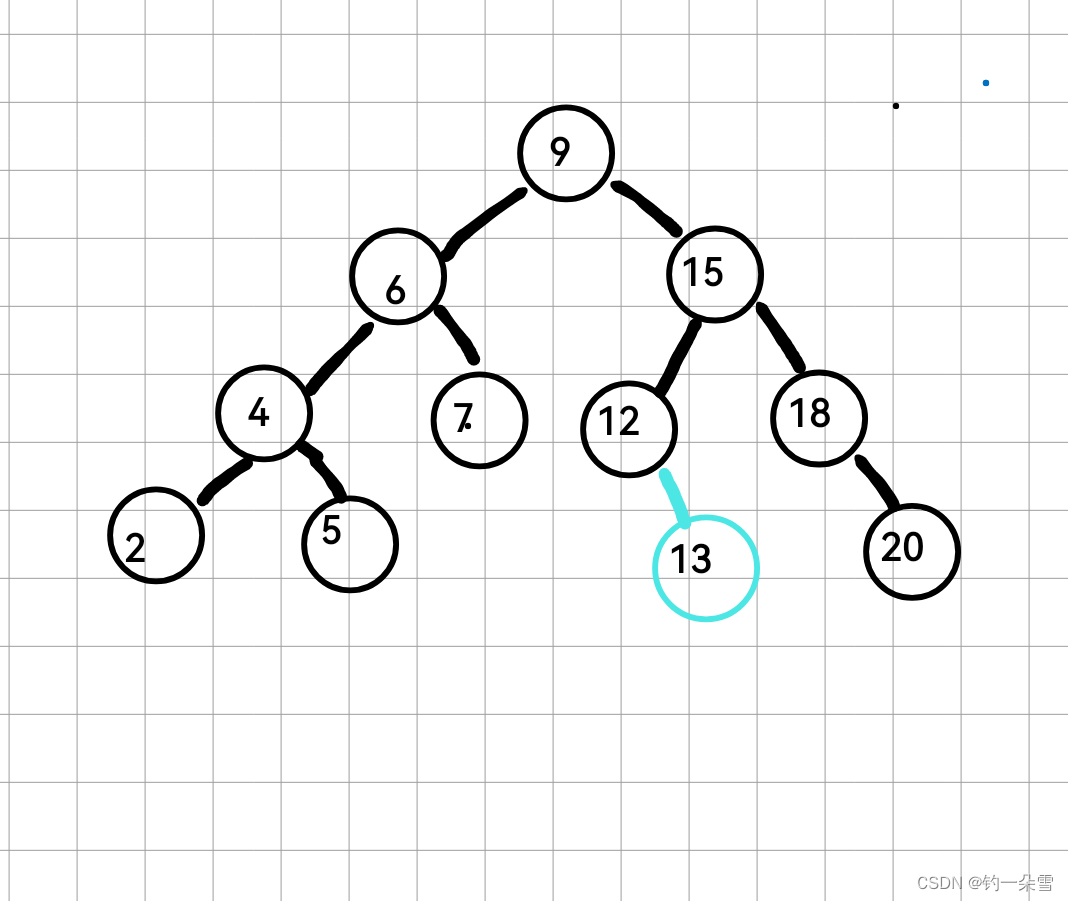
如图所示插入节点13,向上更新parent的平衡因子,节点12的平衡因子由0—>1
节点15的平衡因子由1—>0,结束平衡因子的更新。
bool Insert(AVL** root, int data)
{
if (!(*root))
{
*root = CreateNode(data);
return true;
}
AVL* cur = *root;
AVL* parent = NULL;
//找
while (cur)
{
if (data > cur->data)
{
parent = cur;
cur = cur->right;
}
else if (data < cur->data)
{
parent = cur;
cur = cur->left;
}
else
return false;
}
cur = CreateNode(data);
//插(左/右)
if (data < parent->data)
{
parent->left = cur;
cur->parent = parent;
/*parent->bf--;*/
/*现在还不是更新平衡因子的时候*/
}
else
{
parent->right = cur;
cur->parent = parent;
/*parent->bf++;*/
/*现在还不是更新平衡因子的时候*/
}
//更新平衡因子
while (cur != *root)
{
if (cur == parent->left)
{
parent->bf--;
}
else
{
parent->bf++;
}
//需要继续向上找
if (parent->bf == 1 || parent->bf == -1)
{
cur = parent;
parent = parent->parent;
//结束
if (parent == NULL || parent->bf == 0)
break;
}
//需要旋转
if (parent->bf == 2 || parent->bf == -2)
{
if (parent->bf == 2)
{
if (cur->bf == 1)
RotateL(parent);
else if(cur->bf == -1)
RotateRL(parent);
}
else if(parent->bf == -2)
{
if (cur->bf == 1)
RotateLR(parent);
else if(cur->bf == -1)
RotateR(parent);
}
}
}
return true;
}
旋转处理
左单旋
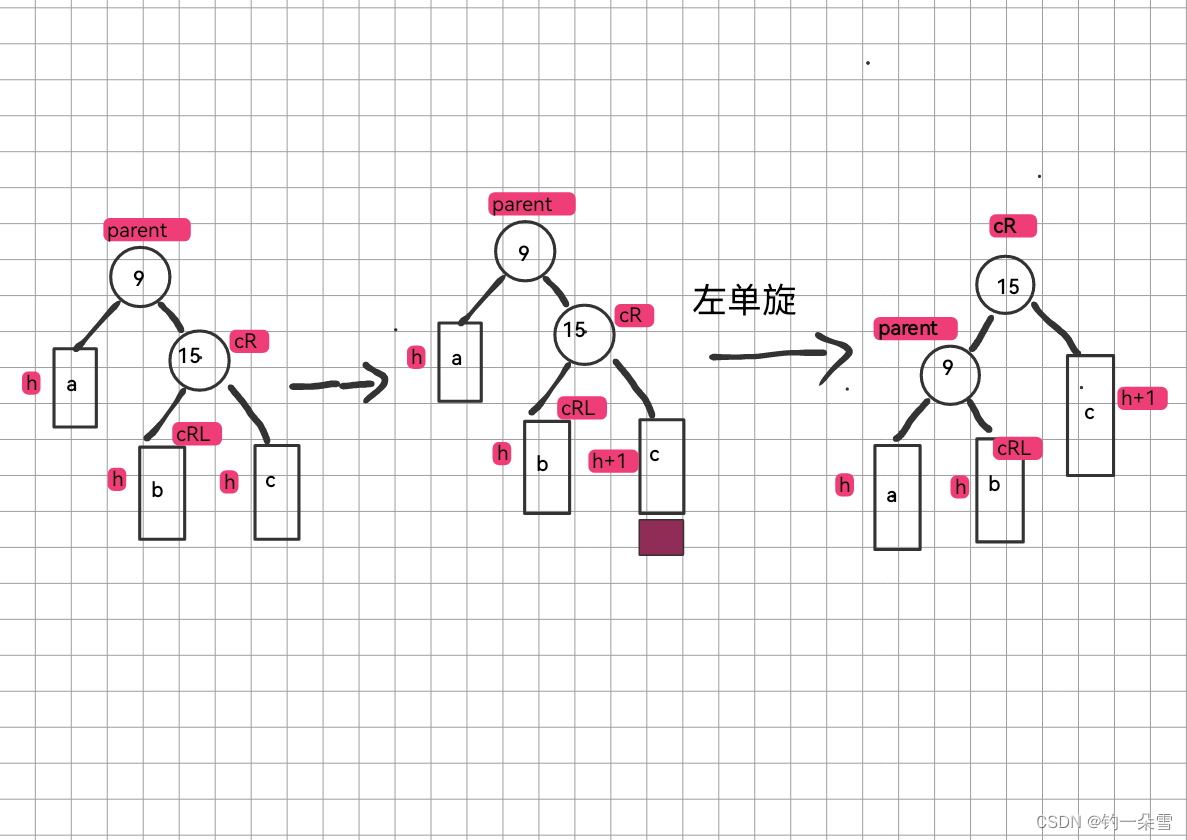
步骤
- cR的左子树作为parent的右子树
- parent成为cR的左子树
- cR成为子树的根
- cR插入到树中
- 更新平衡因子
右单旋
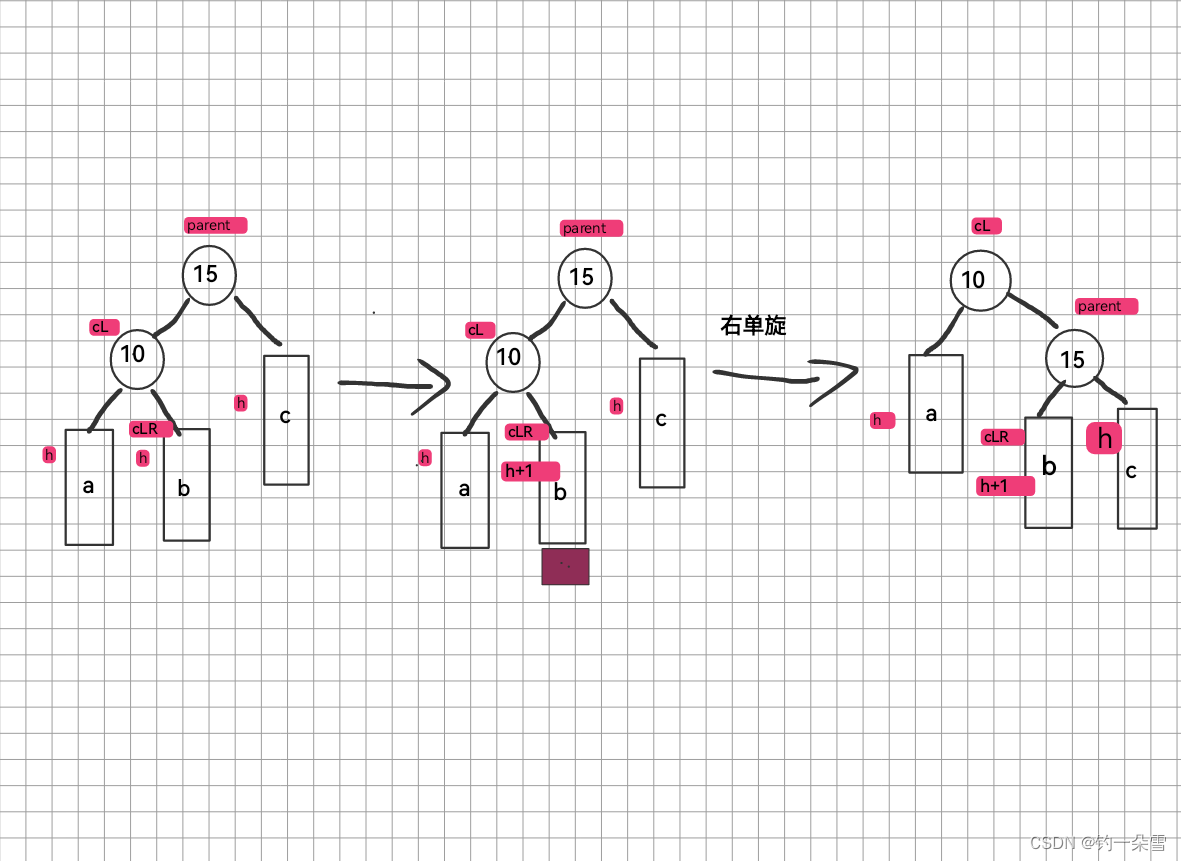
步骤
- cL的右子树成为parent的左子树
- parent成为cL的右子树
- cL成为子树的根
- cL插入到树中
- 更新平衡因子
左右单旋
插入节点
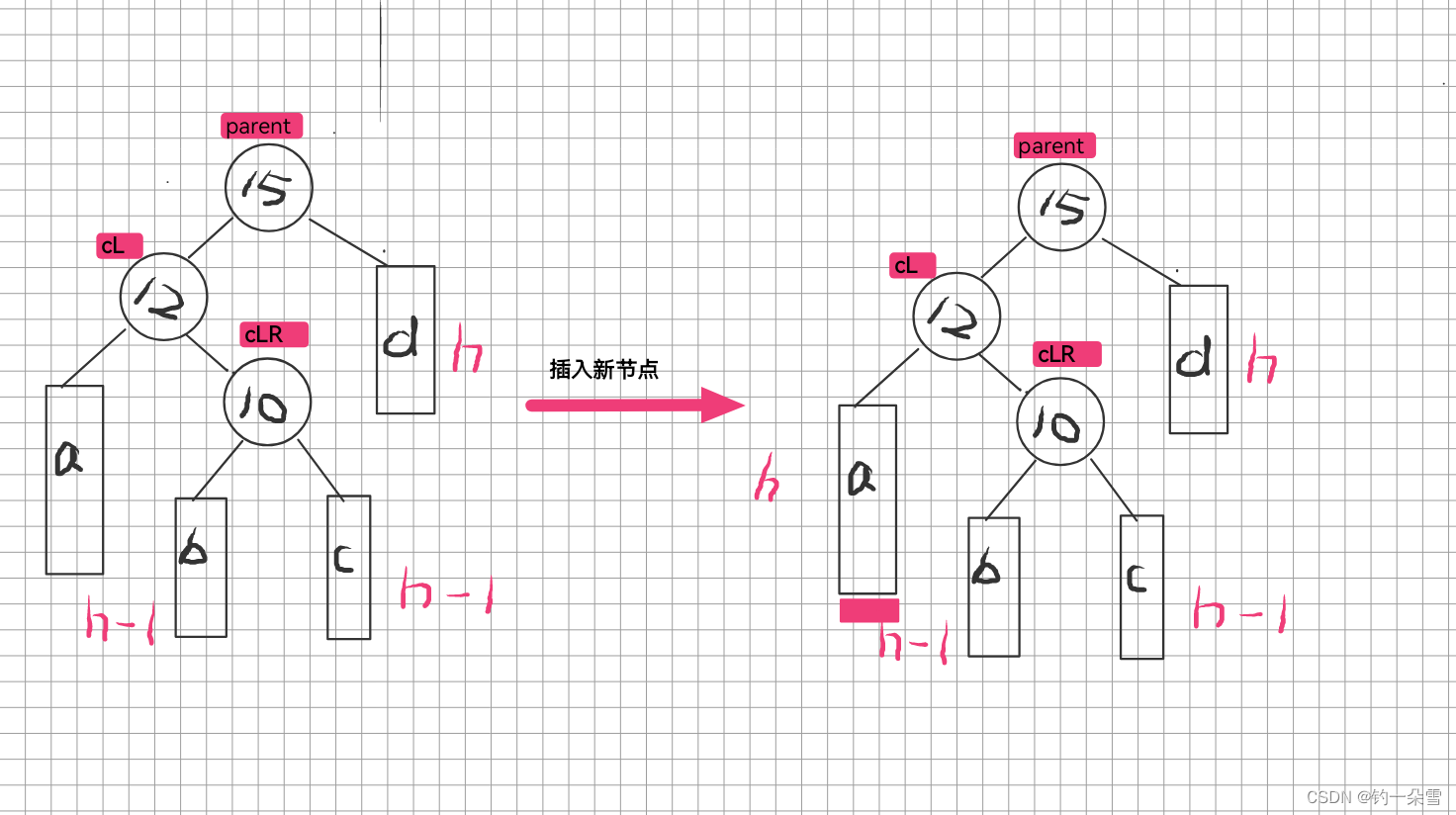
左单旋
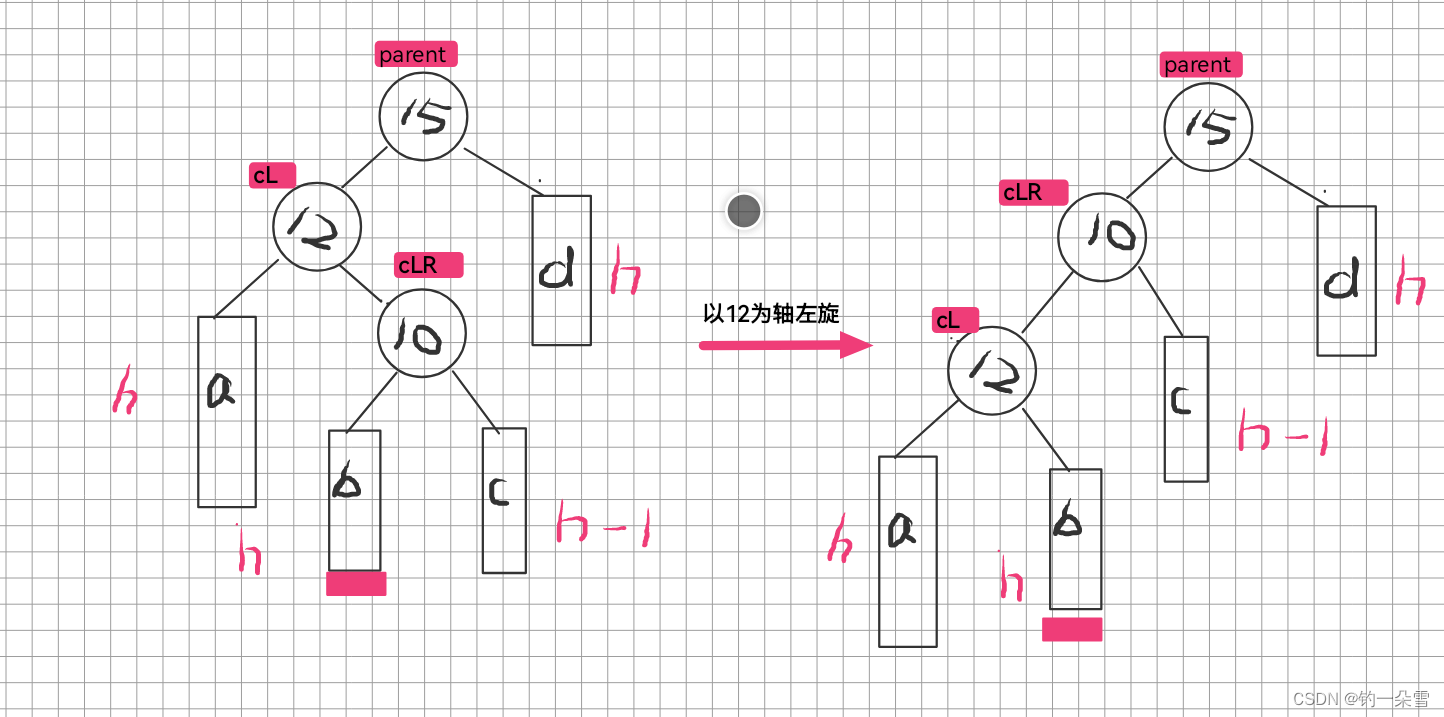
右单旋
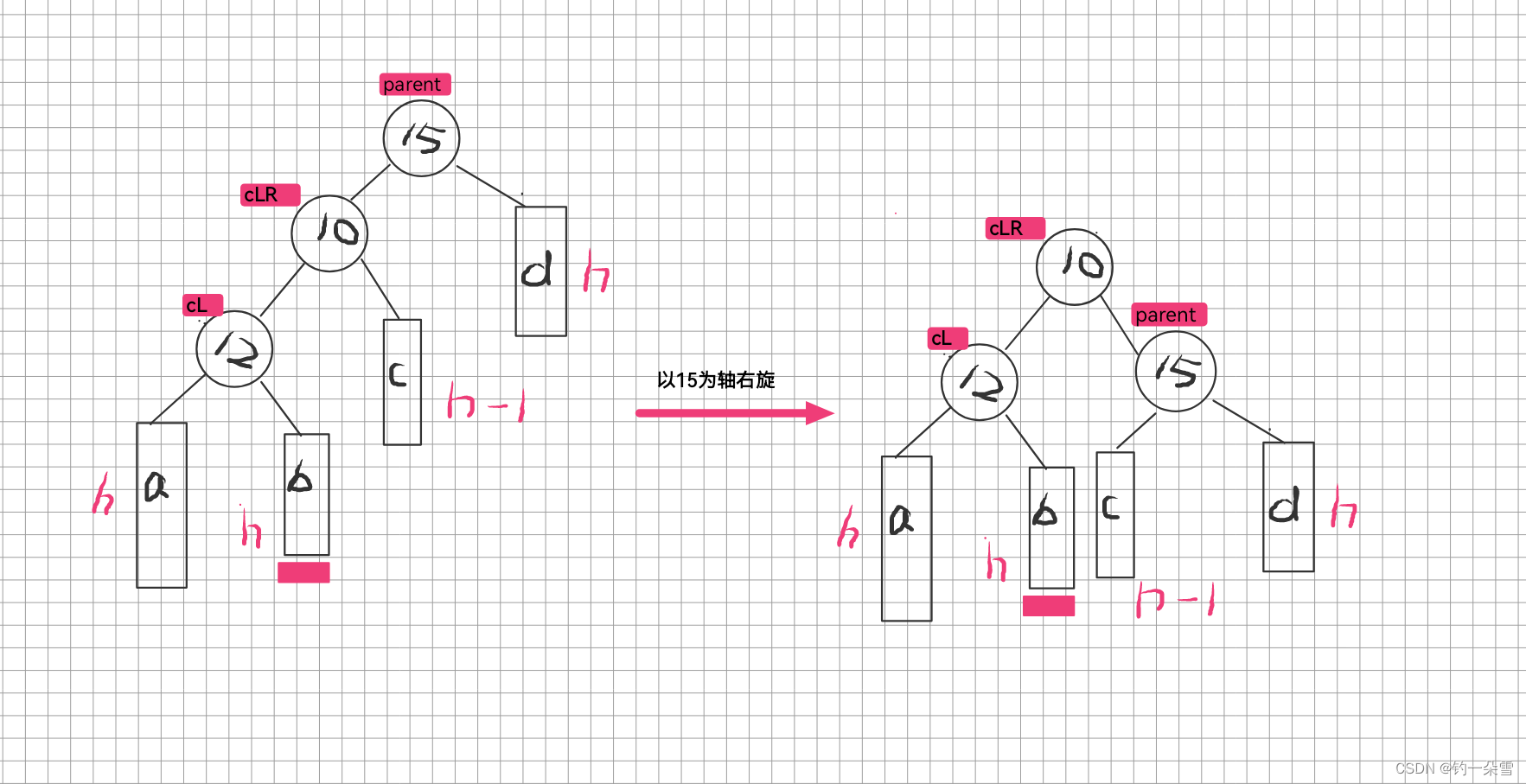
平衡因子更新的三种情况
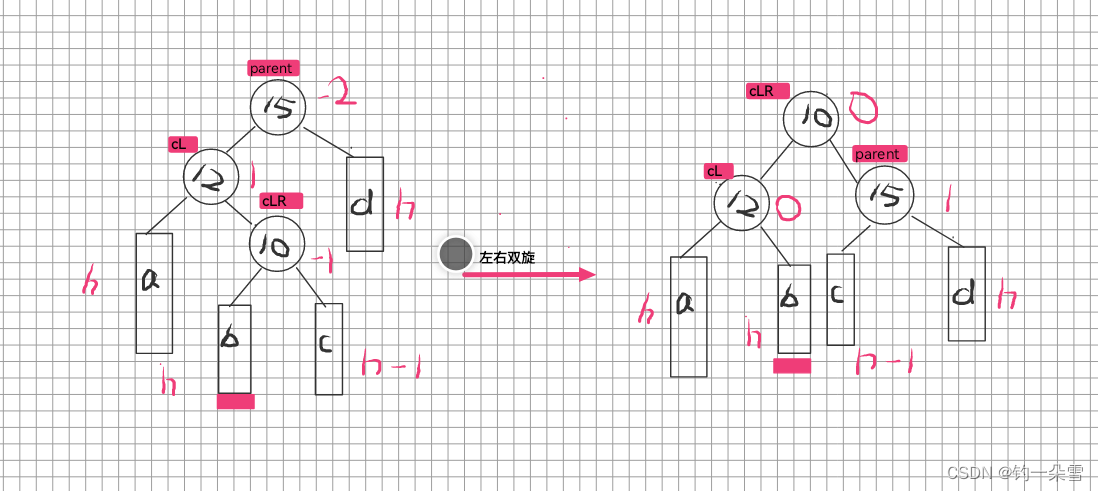
2.
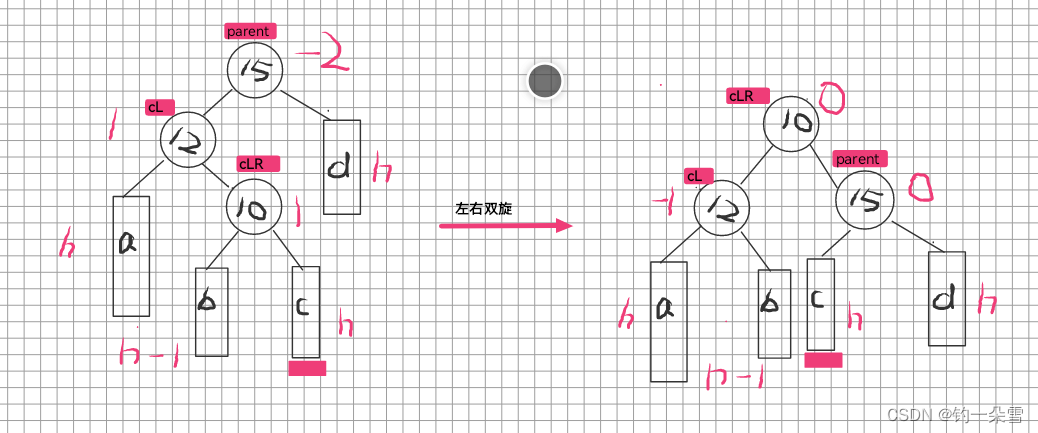
3.
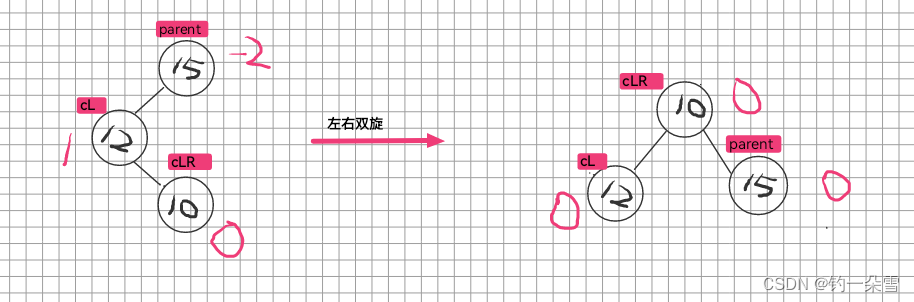
右左单旋
插入节点
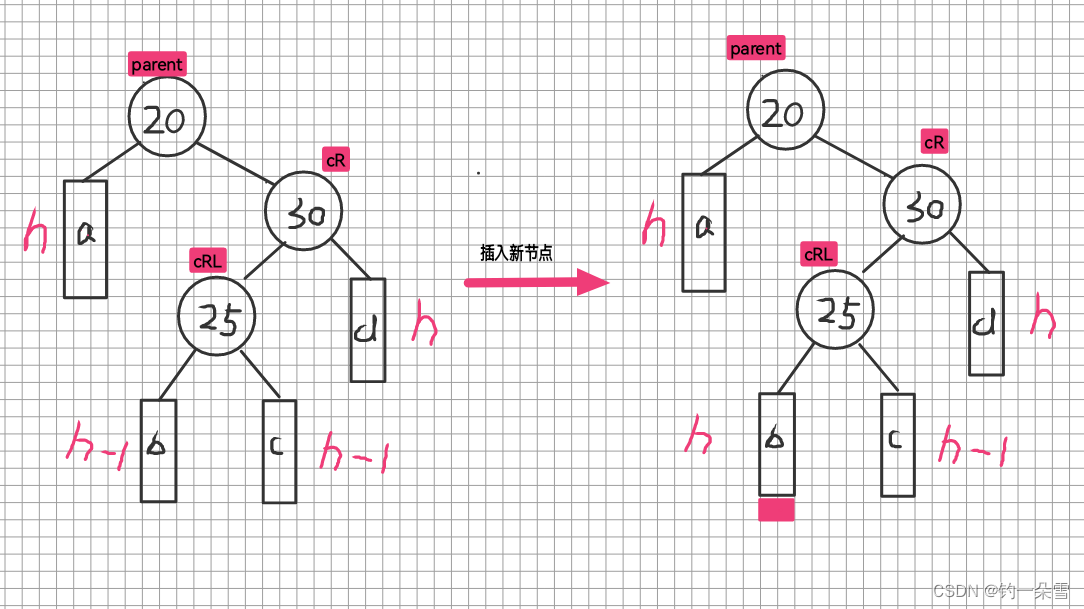
右单旋
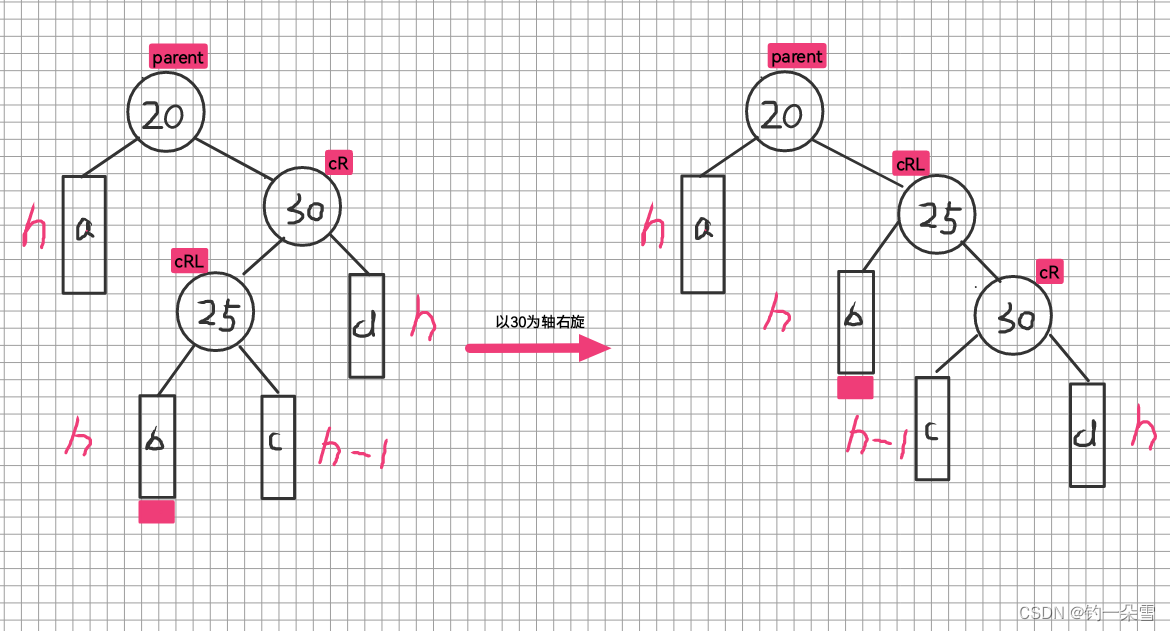
左单旋
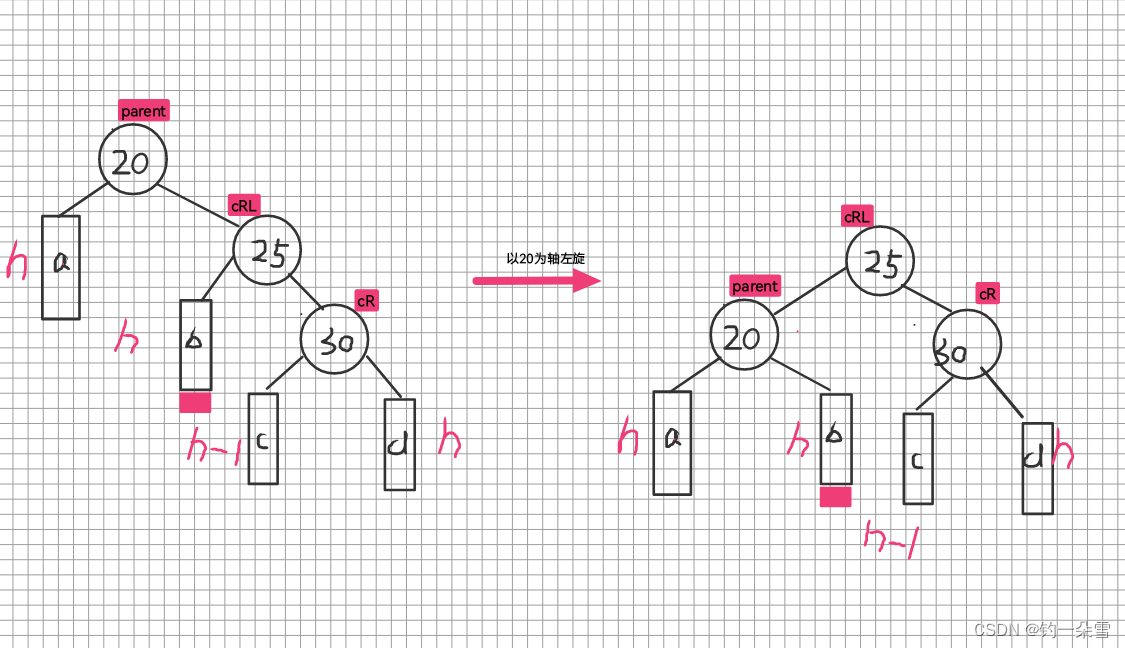
void RotateRL(AVL* parent)
{
AVL* cR = parent->left;
AVL* cRL = cR->right;
int bf = cRL->bf;
RotateR(cR);
RotateL(parent);
//更新平衡因子
if (bf == 1)
{
parent->bf = -1;
cR->bf = 0;
cRL->bf = 0;
}
if (bf == 0)
{
parent->bf = 0;
cR->bf = 0;
cRL->bf = 0;
}
if (bf == -1)
{
parent->bf = 0;
cR->bf = 1;
cRL->bf = 0;
}
}
验证平衡二叉树
平衡二叉树是一种加了平衡限制的二叉查找树,所以通过中序遍历可以验证是否为一颗二叉查找树。通过后序遍历,从叶子节点开始获取每个节点左右子树的高(以该节点为根的子树高为 左右子树中高度的较大值 + 1)
bool isBalanced(AVL* root, int* phight)
{
if (root == NULL)
{
return true;
}
int leftHight = 0;
if (isBalanced(root->left, &leftHight) == false)
return false;
int rightHight = 0;
if (isBalanced(root->right, &rightHight) == false)
return false;
/*if (rightHight - leftHight != root->bf)
printf("平衡因子设置异常\n");*/
*phight = MAX(leftHight, rightHight) + 1;
return abs(rightHight - leftHight) < 2;
}