Problem - E - Codeforces

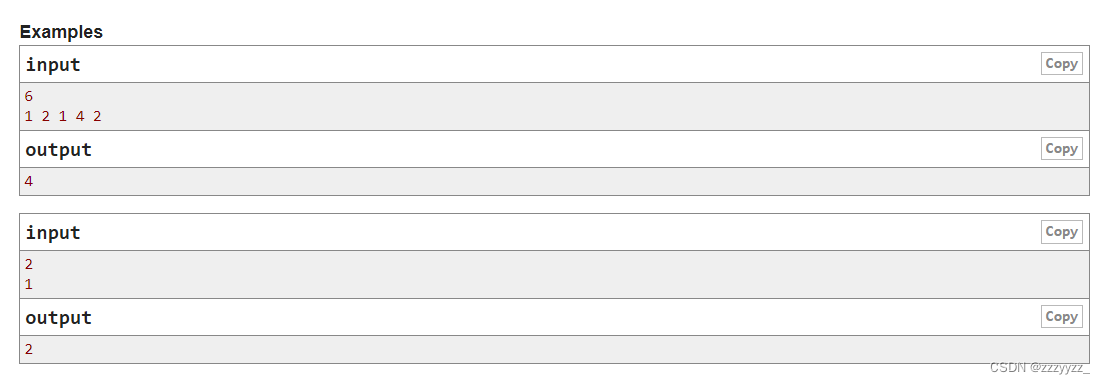
思路：我们考虑用树形dp，用f[i][0]表示以i为根，并且当前节点不在最长上升子序列中，用f[i][1]表示以i为根，当前节点在最长上升子序列中，那么f[i][0]+=max(f[j][0],f[j][1])，因为对于以i为根的子树来说，i的所有子节点组成的子树是没有关联的，所以不包含当前节点的最长上升子序列就是每个子节点的最长上升子序列的和，f[i][1]=max(f[i][1],f[j][1]+1)，如果包含当前节点，因为我一定是在删除了所有的子节点之后才删除当前节点，所以我这个节点的值一定是子节点中除1之外的最小的值，并且它只有其中的某一个子节点能够等于这个值，那么我们为了让它最大，肯定是挑路径最长的那个子节点的值等于这个值，这样就能够让f[i][1]最大，所以f[i][1]只需要找以i为根的最长的路径就可以

// Problem: E. Hanging Hearts
// Contest: Codeforces - Codeforces Round 831 (Div. 1 + Div. 2)
// URL: https://codeforces.com/problemset/problem/1740/E
// Memory Limit: 256 MB
// Time Limit: 1000 ms

#include<iostream>
#include<cstring>
#include<string>
#include<sstream>
#include<bitset>
#include<deque>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<cassert>
#include<queue>
#include<map>
#include<stack>
#include<vector> 
#include<set>
#include<cstdlib>
#define fi first
#define se second
#define i128 __int128
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> PII;
typedef pair<int,pair<int,int> > PIII;
const double eps=1e-7;
const int N=5e5+7 ,M=5e5+7, INF=0x3f3f3f3f,mod=1e9+7,mod1=998244353;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template<typename T> T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template<typename T> T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}

int T,hackT;
int n,m,k;
vector<int> h[N];
int f[N][2];

void dfs(int u,int fa) {
	f[u][1]=1;
	for(int i=0;i<h[u].size();i++) {
		int j=h[u][i];
		
		if(j==fa) continue;
		dfs(j,u);
		f[u][0]+=max(f[j][0],f[j][1]);
		f[u][1]=max(f[u][1],f[j][1]+1);
	}
}

void solve() {
	n=read();
	
	for(int i=2;i<=n;i++) {
		int c=read();
		h[c].push_back(i);
		h[i].push_back(c);
	}
	
	dfs(1,-1);
	
	printf("%d\n",max(f[1][0],f[1][1]));
}   

int main() {
    // init();
    // stin();
	//ios::sync_with_stdio(false); 

    // scanf("%d",&T);
    T=1; 
    while(T--) hackT++,solve();
    
    return 0;       
}