本期为大家带来的是:自适应t分布变异的黏菌优化算法。分别在CEC2005,CEC2017,CEC2021和CEC2022上进行测试,自适应t分布变异的黏菌优化算法(DTSMA)均有非常不错的表现!大家可以将此文章中提到的改进策略用于别的智能算法的改进。
参考文献:Yin S,Luo Q,DU Y.DTSMA: Dominant Swarm with Adaptive T-distribution Mutation-based Slime Mould Algorithm.Mathematical Biosciences and Engineering : MBE, 01 Jan 2022, 19(3):2240-2285https://doi.org/10.3934/mbe.2022105
文献原文已打包放在压缩包中,后台回复关键词获取。
原理详解
黏菌算法(SMA)是受黏菌振动的启发而提出的一种元启发式算法。与其他算法相似,SMA算法也存在着探索与开发不够平衡、容易陷入局部最优等缺点。此文献提出了一种改进的基于自适应t分布突变的黏菌算法。在DTSMA中,利用优势群体提高了SMA的收敛速度,利用自适应t分布突变平衡增强了算法的探索和开发能力。此外,还混合了一种新的开发机制,增加了种群的多样性。
改进点有三处:
改进点1
在求解优化问题的过程中,SMA没有利用黏菌个体最优位置的信息来更新解,可能会错过寻找全局最优的好机会。在DTSMA中,为了记录个体历史最优位置信息,定义优势群体X及其适应度值S来存储历史最优信息。位置更新后,将更新后的位置X与优势群体中的位置Xgood进行比较,采用贪婪选择策略将较优的位置保留给优势群体。在探索阶段,DTSMA使用迄今为止找到的个体历史最优和种群历史最优共同更新搜索个体位置X。更新黏菌位置的公式如式所示。
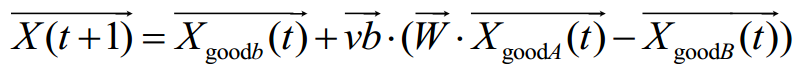
SMA对每次迭代中的个体适应度值进行排序,以找到最优和最差适应度。排序过程很耗时,为了更好地利用排序后的个体位置和适应度值,DTSMA将排序后的种群分为两个子种群,适应度值排名上半部分的种群为goodA X,另一个种群为goodB X。取A和B的值为:
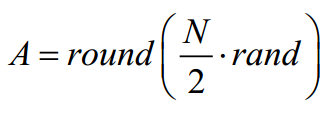
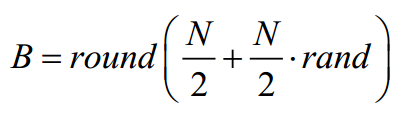
改进点2
SMA具有较强的开发能力,但较弱的勘探能力。该算法容易陷入局部最优,出现过早收敛现象。为了平衡探索和开发,在优势群体再生后增加了突变机制。将高斯突变和柯西突变之间的t分布突变切换应用于SMA。t分布突变的自由度随迭代次数自适应变化,可以很好地平衡SMA的探索和利用。当自由度较大时,t分布接近高斯分布,当自由度为1时,为柯西分布。
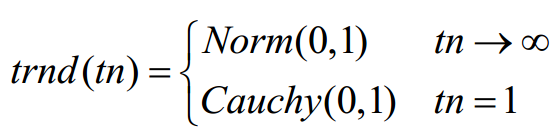
t分布突变算子的数学表达式为
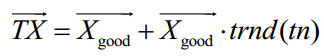
在DTSMA中,自由度参数tn随迭代次数t呈非线性增长。

自由度参数tn使DTSMA能够在早期迭代中近似使用柯西突变来增强探测能力,在后期迭代中近似使用高斯突变来集中开发能力。在DTSMA迭代过程中,随着自由度tn的增加,算法逐渐从关注全局探索能力向关注局部开发能力转变。
改进点3
在DTSMA的开发阶段增加搜索算子,以增加黏菌种群的多样性。开发算子表示为
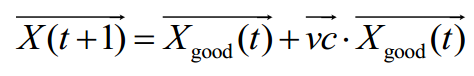
该算子给出了黏菌的搜索代理最终会停在当前找到的最优位置,并且在某些情况下,个别最优可能收敛到当前全局最优位置goodb X之外。基于上述原理,位置更新的数学公式为:
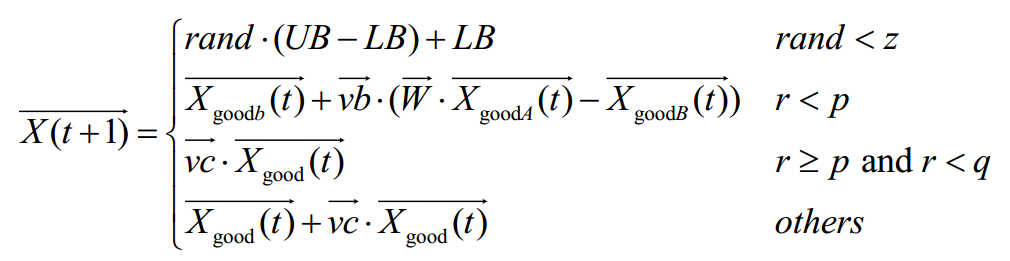
结果展示
本期分别在CEC2005,CEC2017,CEC2021和CEC2022进行详细测试。测试结果如下。
CEC2005: 这里直接上几个比较经典的测试函数。
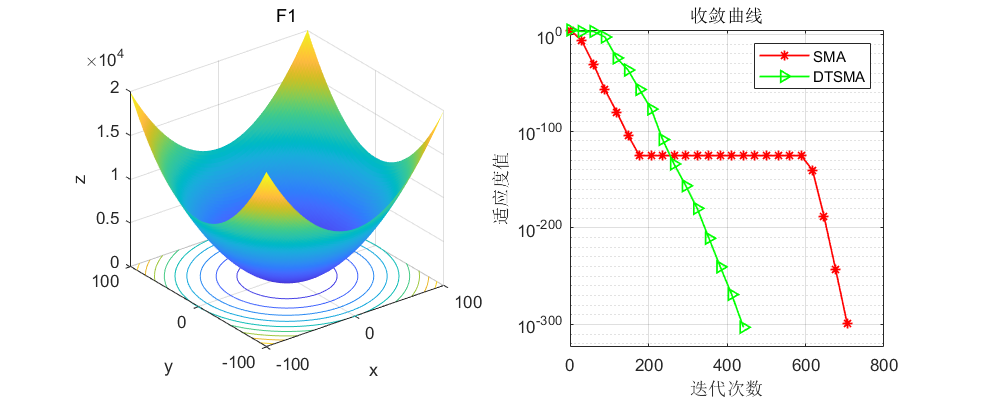
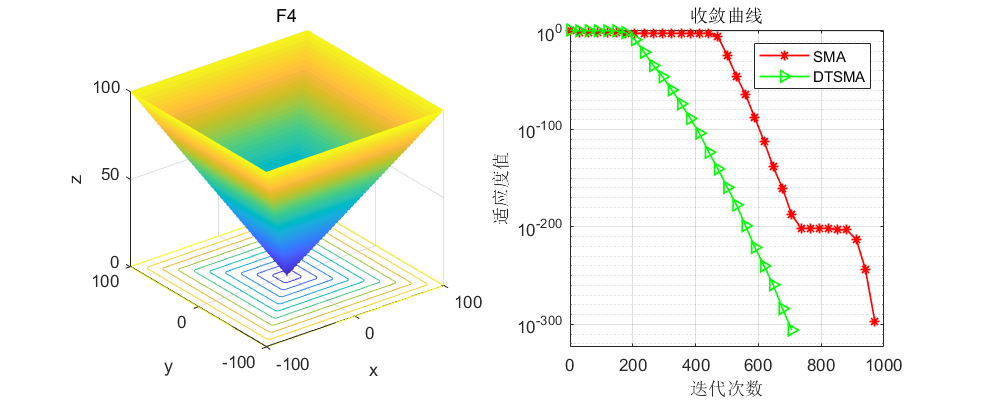
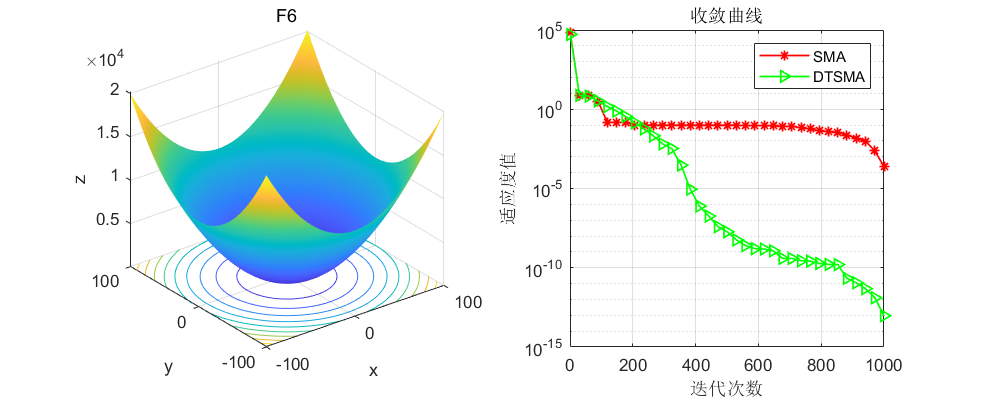
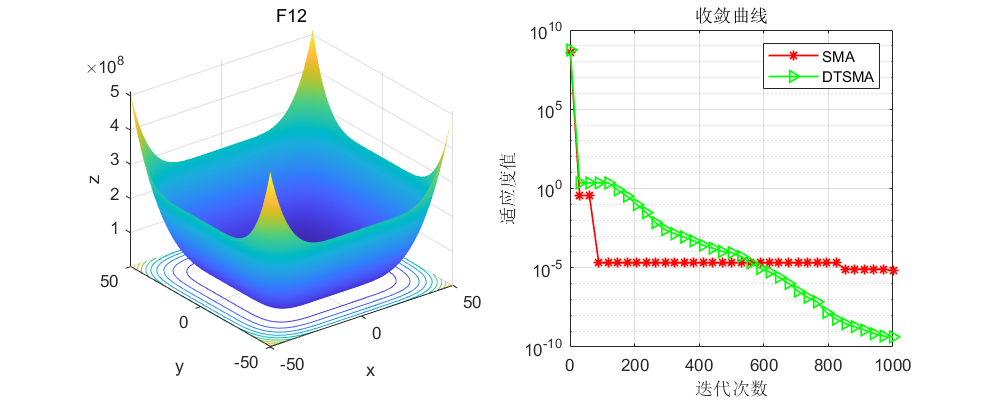
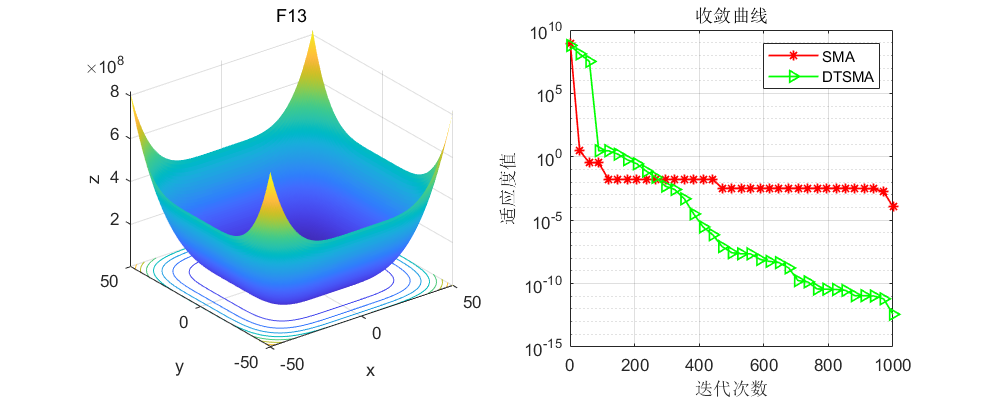
CEC2017:
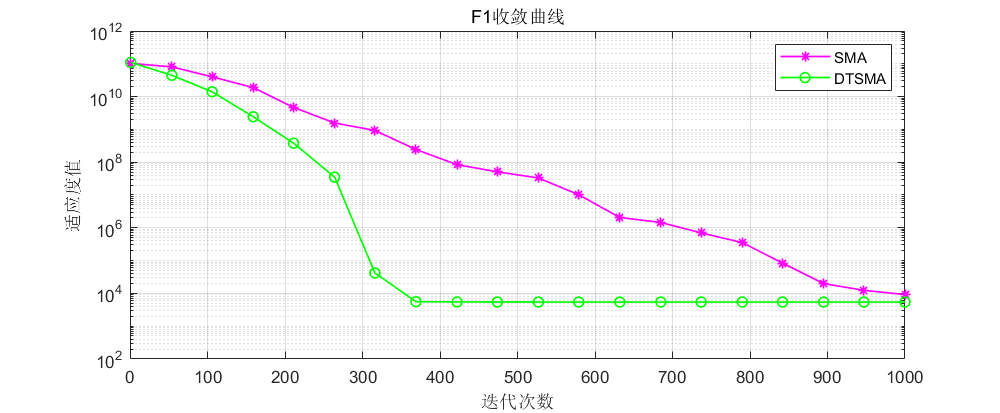
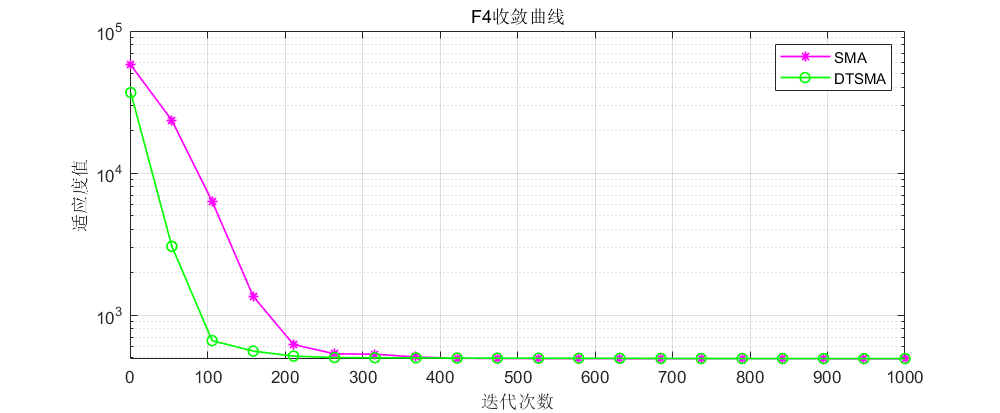
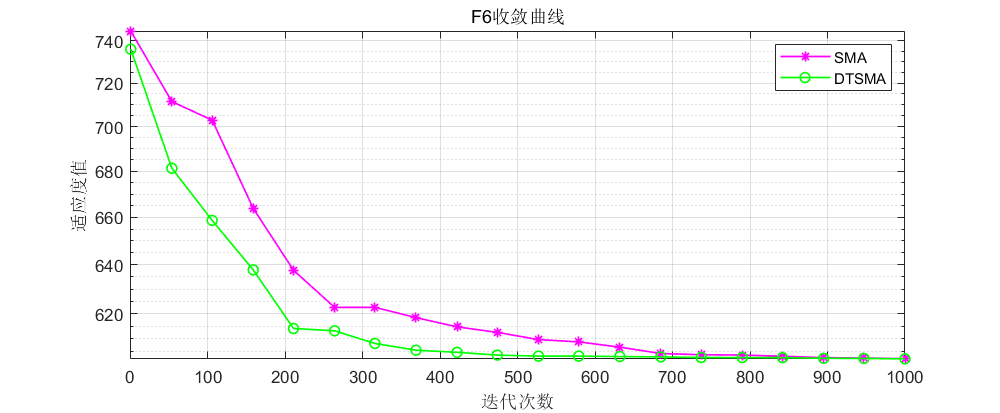
CEC2021:
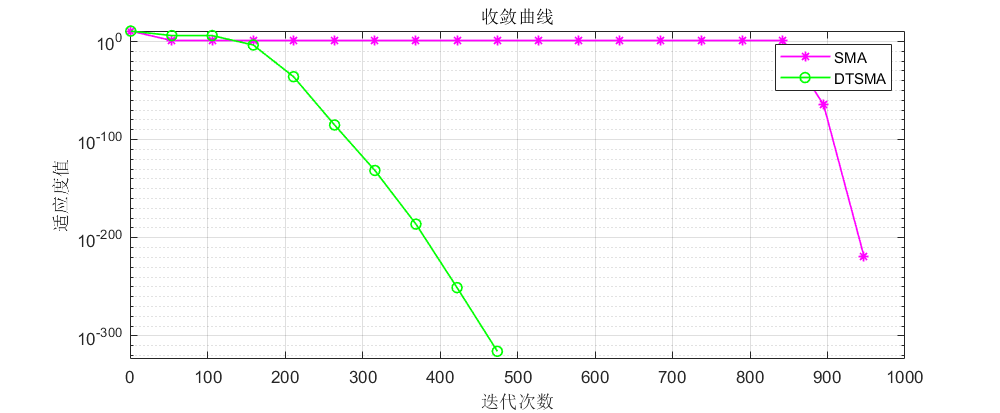
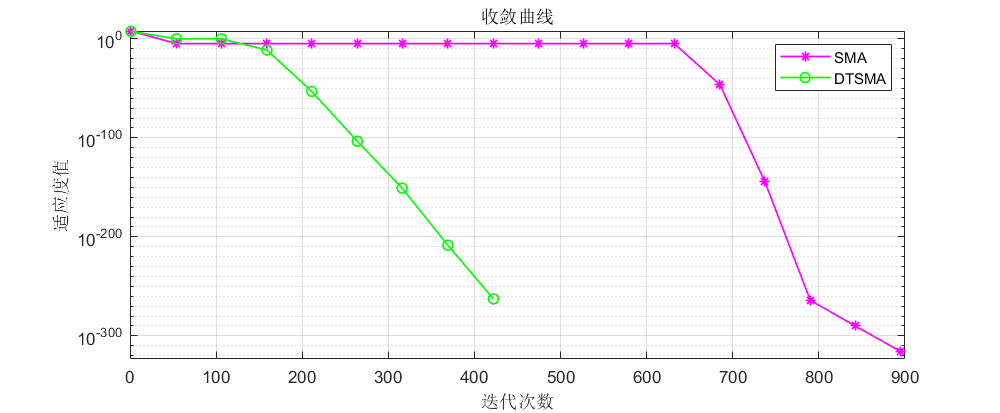

CEC2022:

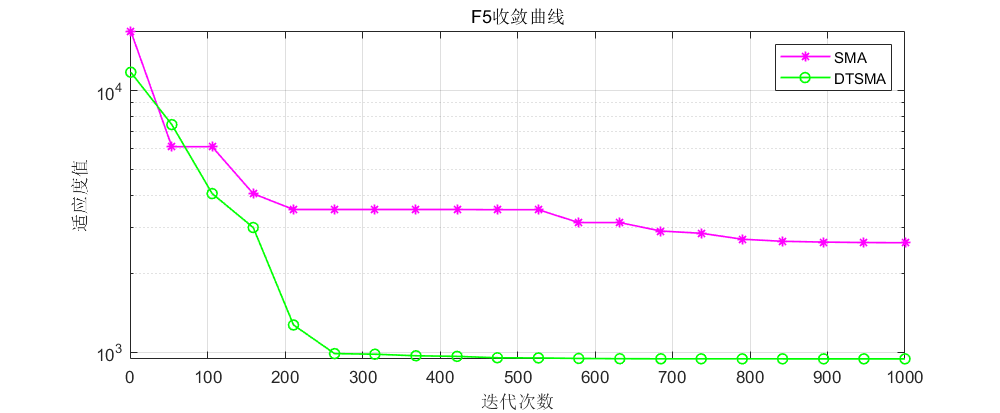
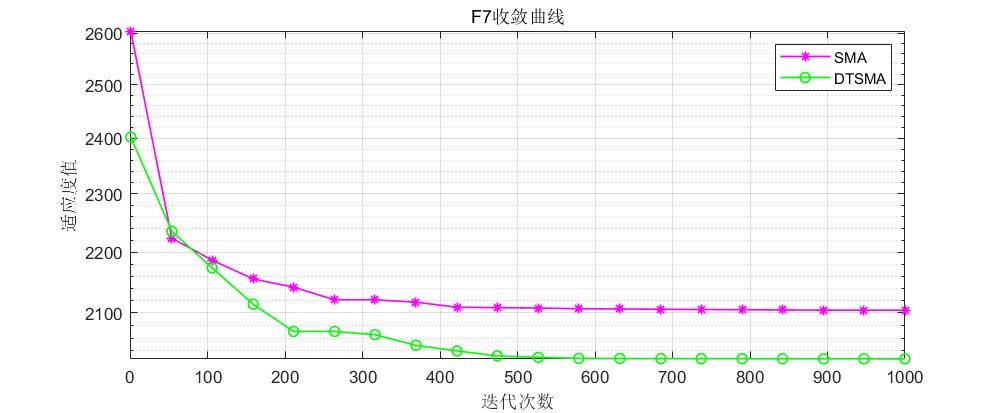
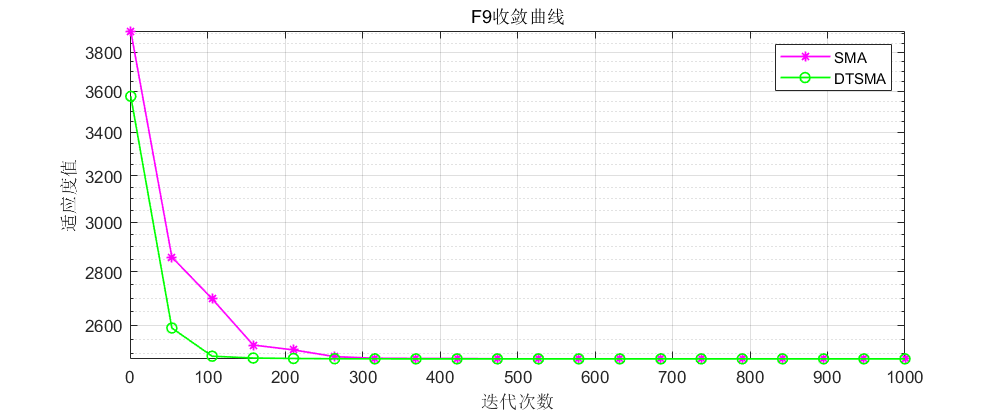
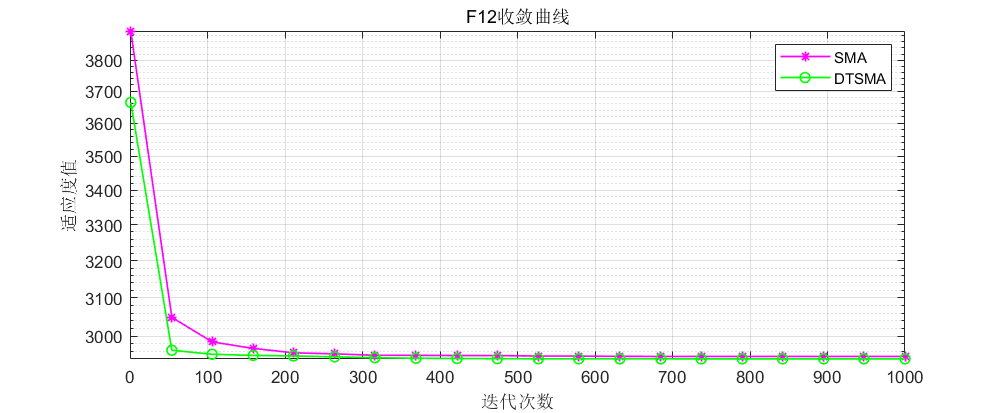
可以看到不论是CEC的哪个测试集,改进的黏菌算法表现都还不错!
代码展示
下面附上黏菌算法的matlab代码
% 黏菌优化算法(SMA)
% max _ iter:最大迭代次数,N:种群大小,收敛曲线:收敛曲线,
function [Destination_fitness,bestPositions,Convergence_curve]=SMA(N,Max_iter,lb,ub,dim,fobj)
%% 初始化位置
bestPositions=zeros(1,dim);
Destination_fitness=inf;%将此更改为 -inf 以解决最大化问题
AllFitness = inf*ones(N,1);%记录所有粘菌的适应度
weight = ones(N,dim);%每个粘菌的适应度权重
%% 初始化随机解集
X=initialization(N,dim,ub,lb);
Convergence_curve=zeros(1,Max_iter);
it=1; %迭代次数
lb=ones(1,dim).*lb; % 变量下限
ub=ones(1,dim).*ub; % 变量上限
z=0.03; % 参数
%% 主循环
while it <= Max_iter
%=====适应度排序======
for i=1:N
% 检查解决方案是否超出搜索空间并将其带回
Flag4ub=X(i,:)>ub;
Flag4lb=X(i,:)<lb;
X(i,:)=(X(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
AllFitness(i) = fobj(X(i,:));
end
[SmellOrder,SmellIndex] = sort(AllFitness);
worstFitness = SmellOrder(N);
bestFitness = SmellOrder(1);
S=bestFitness-worstFitness+eps; %加上 eps 以避免分母为零
%====计算每个粘菌的适应度权重=====
for i=1:N
for j=1:dim
if i<=(N/2)
weight(SmellIndex(i),j) = 1+rand()*log10((bestFitness-SmellOrder(i))/(S)+1);
else
weight(SmellIndex(i),j) = 1-rand()*log10((bestFitness-SmellOrder(i))/(S)+1);
end
end
end
%====更新最佳适应度值和最佳位置=====
if bestFitness < Destination_fitness
bestPositions=X(SmellIndex(1),:);
Destination_fitness = bestFitness;
end
a = atanh(-(it/Max_iter)+1);
b = 1-it/Max_iter;
%====更新搜索代理的位置=====
for i=1:N
if rand<z
X(i,:) = (ub-lb)*rand+lb;
else
p =tanh(abs(AllFitness(i)-Destination_fitness));
vb = unifrnd(-a,a,1,dim);
vc = unifrnd(-b,b,1,dim);
for j=1:dim
r = rand();
A = randi([1,N]); % 从总体中随机选择两个位置
B = randi([1,N]);
if r<p
X(i,j) = bestPositions(j)+ vb(j)*(weight(i,j)*X(A,j)-X(B,j));
else
X(i,j) = vc(j)*X(i,j);
end
end
end
end
Convergence_curve(it)=Destination_fitness;
% display(['At iteration ', num2str(it), ' the best solution fitness is ', num2str(Destination_fitness)]);
it=it+1;
end
end完整代码获取
自适应t分布变异的黏菌优化算法MATLAB代码,参考文献和四种CEC函数集测试均已打包在压缩包中了,目录展示如下:

完整代码获取方式,后台回复关键词。关键词:
DTSMA











![[移动通讯]【Carrier Aggregation-4】【LTE-2】](https://img-blog.csdnimg.cn/959ee365f0cf4f3884d02f14a9e1bdf7.png)