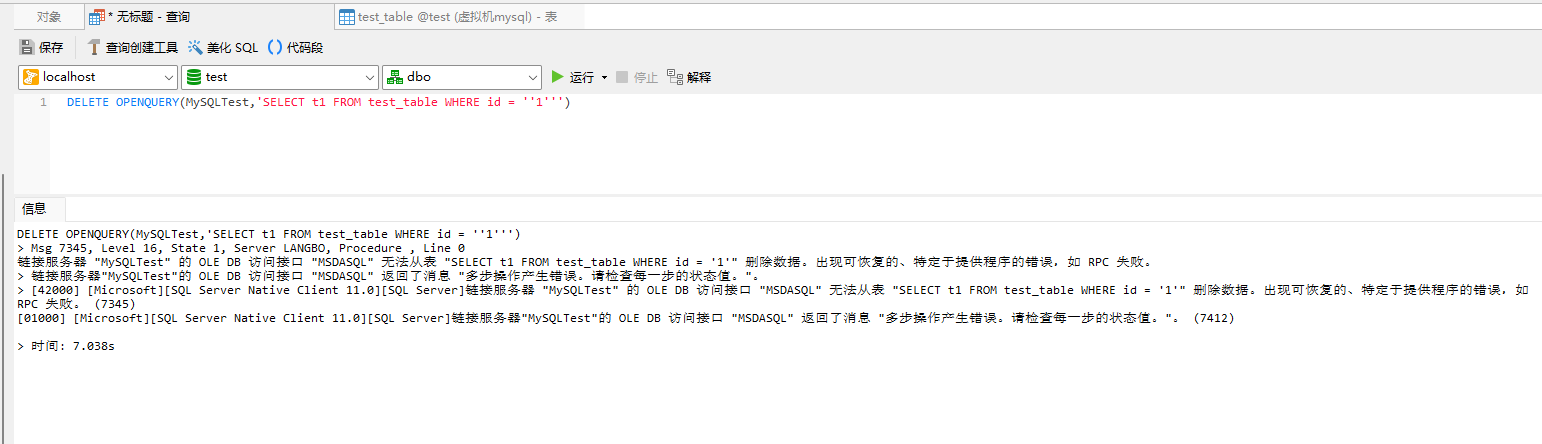
机器学习算法详解2:线性回归
前言
本系列主要对机器学习上算法的原理进行解读,给大家分享一下我的观点和总结。
本篇前言
本篇对线性回归的算法原理进行解读。
目录结构
文章目录
- 机器学习算法详解2:线性回归
- 1. 引子
- 2. 原理
- 3. 特点
- 4. 问题解答
- 4.1 问题1
- 4.2 问题2
- 4.3 问题3
- 5. 广义线性回归
- 6. 岭回归与lasso回归
- 7. 总结
1. 引子
我们有这样的数据:(瞎编的)
| 薪资/万元每年 | 所住房子价格/万元 |
|---|---|
| 10 | 100 |
| 20 | 150 |
| 30 | 300 |
| 50 | 500 |
| 100 | 1000 |
画出图如下:

那么,问题是:如果一个人的工资是60万每年,那么他所住的房价大概在多少?这个问题很好解决,我们从图中可以看出数据符合线性分布,我们可以画一条直线拟合这些数据点,然后代入新数据60,就可以得出对应的结果,如下图所示:

如何求出这条直线就是线性回归要解决的问题。
2. 原理
线性回归分为二元线性回归和多元线性回归,同时也是一个数学解释性非常强的算法,也因此通常作为第一个学习的机器学习算法。
公式推导过程如下:(需要一点点矩阵微分的知识+矩阵可逆判定知识)

3. 特点
线性回归的主要特点是:
- 抗冗余
y = w1 * x1 + w2 * x2 + b
假设x1与x2特征相同,那么可以变化为:y = (w1+w2)x1 + b = wx + b
- 抗噪声
y = w1 * x1 + w2 * Δ + b
假设Δ为噪声,那么学习完成后w2=0,结果为y = w1*x1 + b
4. 问题解答
4.1 问题1
问题:为什么损失函数不用MAE?
假设有以下的数据值:
| y-yi | MAE | MAE间差值 | MSE | MSE间差值 |
|---|---|---|---|---|
| 5 | 5 | 25 | ||
| 4 | 4 | 1(5-4) | 16 | 9 |
| 3 | 3 | 1(4-3) | 9 | 7 |
| 2 | 2 | 1 | 4 | 5 |
| 1 | 1 | 1 | 1 | 3 |
不难从上表看出,MAE并没有倾向性,MSE具有倾向性。可以这么解释,对于机器学习模型来说,学习数据,肯定是先学习到那些容易学习到的性质,当学习到一定程度,如果再继续学已经学习过的知识收益肯定变小了,而对于MAE而言,他感受不到收益变小了,因为每次学习的知识都差1,但是对于MSE而言,就可以明显感觉到收益降低,因此它会主动去学习新知识以提高收益。
4.2 问题2
问题:对于线性回归而言,是不是拟合函数y=w0*x+w1*x2+w2*x3…越多越好?
答:是的,可以这么解释:
y1 = w0 * x + w1 * x^2
y2 = w0 * x
对于y1而言,只要w1=0就退化到了y2,自然y1的性能至少都要比y2好
4.3 问题3
问题:这里线性回归不是求解出来了解析解吗?为什么sklearn库实现那些算法仍然是通过梯度优化算法呢?
其实,如果让你我来实现线性回归,肯定是用解析解来实现的。但是对于写库的人来说,肯定需要考虑到通用性,他只需要写一个通用的梯度算法就可以实现绝大部分算法的优化。
因此,对于有解析解的算法,你可以自己从底层来实现它,也可以选择使用梯度下降算法来实现它。
5. 广义线性回归
如下图所示:

可以明显看出这个拟合曲线应该是:y=w1x^2 + w2x + w0,我们可以令x^2=A,x=B,那么曲线变为y=w1A+w2B+w0,此时变为了直线方程,将该直线称之为广义线性回归。
由这个思路,可以推导出逻辑回归这个算法的出现。
6. 岭回归与lasso回归
在上一篇中讲解了正则化的知识,而对于线性回归引入正则化公式,就得到了岭回归和lasso回归,损失函数分别如下:(图来自此)

两者的区别可以我这篇博客:《深入机器学习1:详解正则表达式》。另外,需要注意的是岭回归还可以解决多元线性回归中矩阵不可逆的现象(同样在这篇文章中进行了解释)。
7. 总结
本篇介绍了线性回归的应用、公式推导、特点以及其推广。线性回归是很简单的算法,但是在实际任务中应用也比较多。
下一篇,介绍逻辑回归。