平台
题目描述
空间中有一些平台。给出每个平台的位置,请你计算从每一个平台的边缘落下之后会落到哪一个平台上。注意,如果某两个平台的某个两边缘横坐标相同,物体从上面那个平台落下之后将不会落在下面那个平台上。平台可能会重叠。
如果有两个平台的高度相同且都可以被落到的话,那么会落到编号靠前的那个平台。
输入格式
第一行有一个数 N N N 表示平台的个数;
接下来 N N N 行每行三个整数 分别是平台的高度 H i H_i Hi,左端点的 X X X 坐标 L i L_i Li,右端点的 X X X 坐标 R i R_i Ri。
其中, 1 ≤ N ≤ 10 3 1 \le N \le {10}^3 1≤N≤103, 0 ≤ H , L , R ≤ 2 × 10 4 0 \le H,L,R \le 2 \times {10}^4 0≤H,L,R≤2×104。
输出格式
输出共 N N N 行,每行两个数,分别表示:
从第 i i i 个平台的左边缘落下后到达的平台序号和右边缘落下以后到达的平台序号。
输入数据中第一个平台的序号是 1 1 1。如果某个平台的某个边缘下面没有平台了,输出 0 0 0。
样例 #1
样例输入 #1
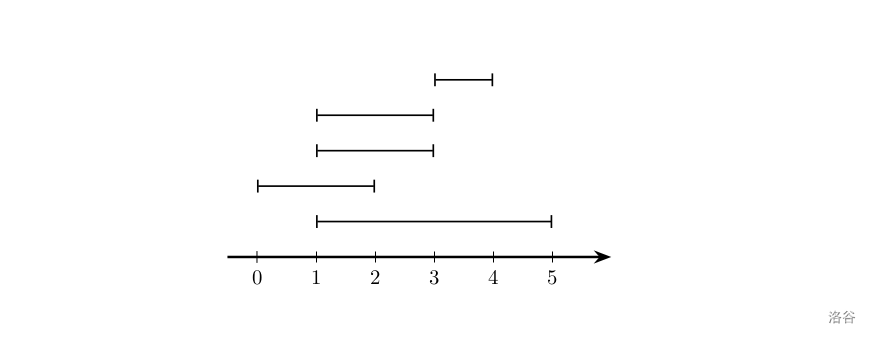
5
2 0 2
4 1 3
3 1 3
5 3 4
1 1 5
样例输出 #1
0 5
1 5
1 5
5 5
0 0
提示
思路
给定一些平台的高度、左右边缘坐标,求出每个平台落地时会落在哪个平台上。
定义了一个S结构体,表示平台的高度、左右边缘坐标和编号。使用sort函数对平台按照高度进行降序排序,然后对每个平台进行处理,求出它落地时会落在哪个平台上。
定义了一个cmp函数,用于对平台进行排序。如果两个平台的高度相同,则将编号小的放在前面,否则按照高度降序排列。
对于每个平台,首先初始化左右边缘的落点和高度,然后从当前平台的下一个平台开始遍历,判断左边缘和右边缘是否可以落到,如果可以则更新对应的落点。最后将每个平台的落点存入到一个pair数组中,按顺序输出即可。
注意:平台可能重叠。如果有两个平台的高度相同且都可以被落到的话,那么会落到编号靠前的那个平台。
AC代码
#include <iostream>
#include <algorithm>
#define AUTHOR "HEX9CF"
using namespace std;
const int maxn = 100005;
struct S
{
int id;
int h;
int l;
int r;
} p[maxn];
// 如果有两个平台的高度相同且都可以被落到的话,那么会落到编号靠前的那个平台。
bool cmp(S x, S y)
{
return (x.h == y.h) ? (x.id < y.id) : (x.h > y.h);
}
int main()
{
int n;
pair<int, int> ans[maxn];
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> p[i].h >> p[i].l >> p[i].r;
p[i].id = i;
}
sort(p + 1, p + 1 + n, cmp);
for (int i = 1; i <= n; i++)
{
int dl, dr;
int hl, hr;
// 初始落点
dl = dr = 0;
for (int j = i + 1; j <= n; j++)
{
// 左边缘落下
if (p[j].l < p[i].l && p[i].l < p[j].r && p[j].h < p[i].h)
{
dl = p[j].id;
break;
}
}
for(int j = i + 1; j <= n; j++) {
// 右边缘落下
if (p[j].l < p[i].r && p[i].r < p[j].r && p[j].h < p[i].h)
{
dr = p[j].id;
break;
}
}
// cout << dl << " " << dr << endl;
ans[p[i].id] = make_pair(dl, dr);
}
for (int i = 1; i <= n; i++)
{
cout << ans[i].first << " " << ans[i].second << endl;
}
return 0;
}