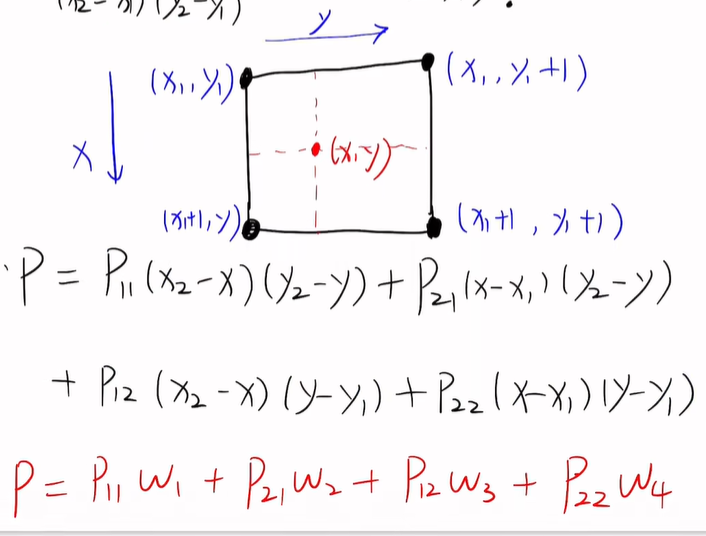参考视频：图像处理-双线性插值_哔哩哔哩_bilibili

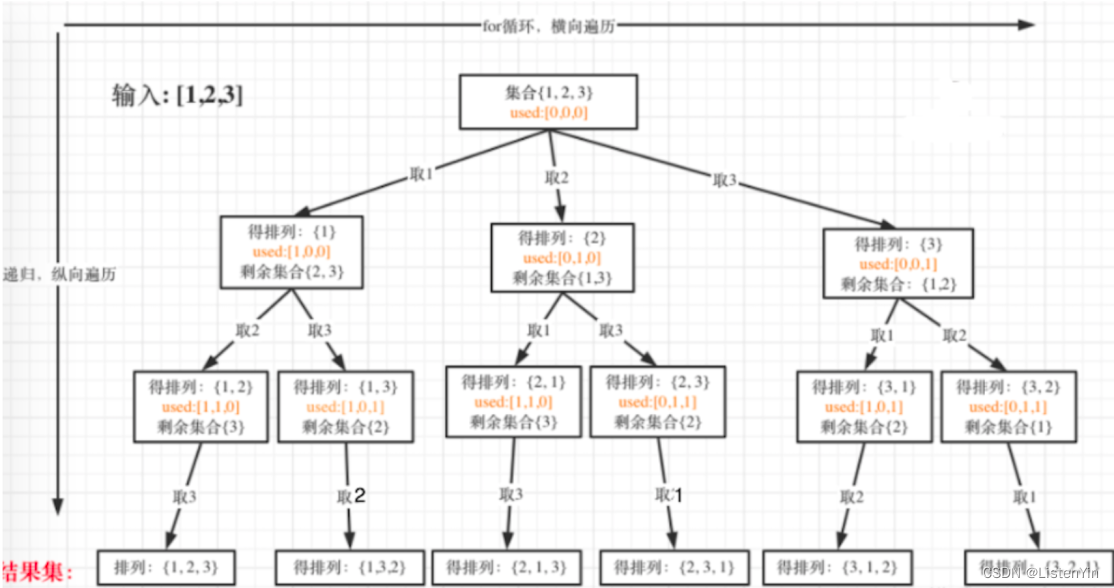
双线性插值

双线性插值是一种常用的图像处理和计算机图形学技术，用于在离散像素网格上平滑地估算介于两个相邻像素之间的数值。这种插值方法通常用于图像放大、旋转和变换等操作，以改善图像的质量和细节。

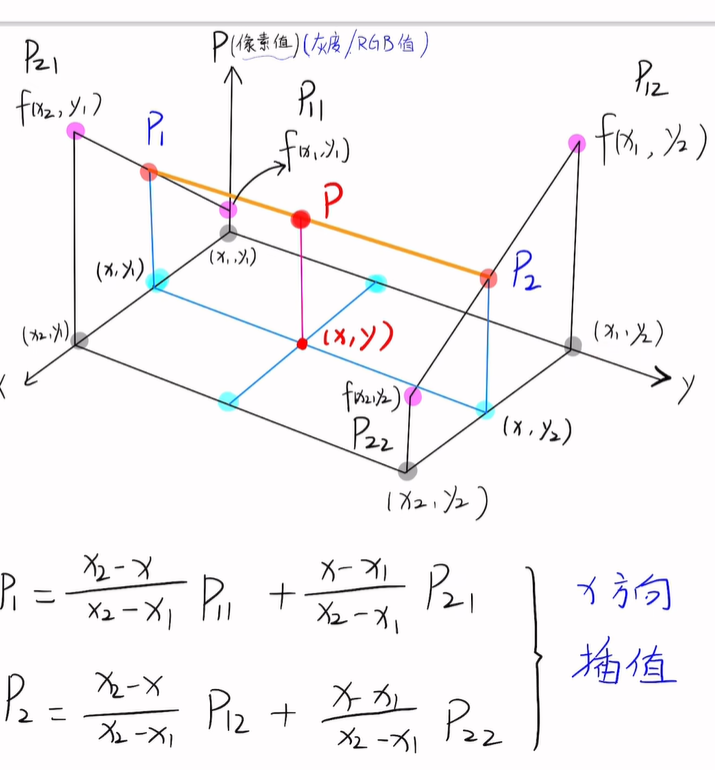
双线性插值的基本思想是，通过考虑目标点周围的四个最近像素（通常是左上、右上、左下和右下四个像素），根据其相对距离和权重来估算目标点的灰度值或颜色值。这四个像素的值根据其与目标点的相对位置和距离以加权平均的方式来计算，从而得到目标点的估值。

这个过程可以用以下公式表示：

f(x, y) = (1 - u)(1 - v)f(x1, y1) + u(1 - v)f(x1, y2) + (1 - u)vf(x2, y1) + uvf(x2, y2)

其中，u = (x - x1)/(x2 - x1)，v = (y - y1)/(y2 - y1)。

f(x1, y1)、f(x1, y2)、f(x2, y1)、f(x2, y2)分别为四个相邻网格点的值。

双线性插值的优点在于它可以在离散像素网格上生成平滑的过渡，减少了锯齿状边缘和失真。这使得图像在放大和变换时看起来更自然和细致。

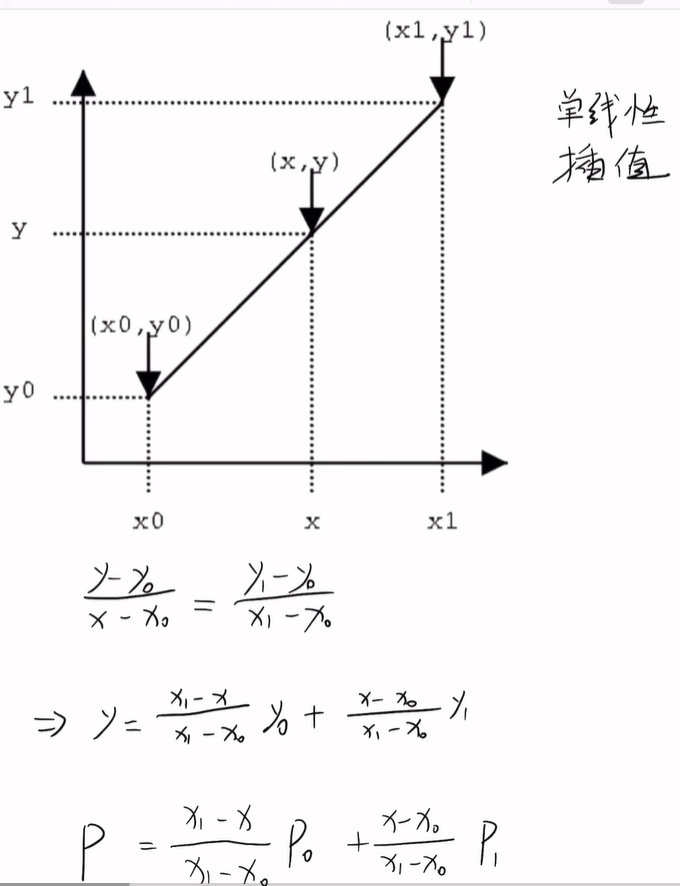
单线性插值

如图所示，x0,y0  x1,y1已知，求x，y

双线性插值

具体步骤

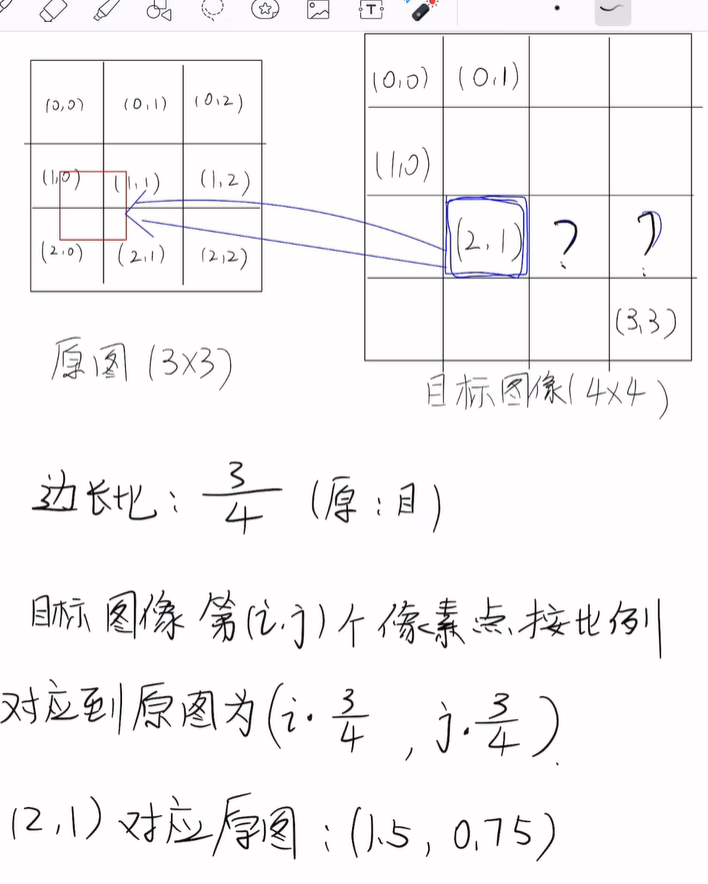
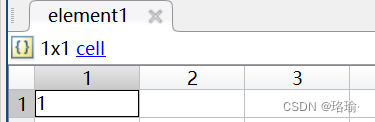
但是（1.5，0.75）是小数，没办法对应上原图中任何一个点，将该方框带入上述公式可以得知↓