回溯法的理解

本文参考了一位大佬的题解，详细的介绍了回溯法：链接

上一篇刷题文： 回溯法经典问题之子集

记住一句话：for循环横向遍历，递归纵向遍历，回溯不断调整结果集。 这句话将从始至终贯穿我们对于以上问题的回溯解决办法。

💮一、字符串的排列

题目链接：剑指 Offer 38. 字符串的排列

题目描述：

输入一个字符串，打印出该字符串中字符的所有排列。

你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

示例:

输入：s = "abc"
输出：["abc","acb","bac","bca","cab","cba"]

限制：

1 <= s 的长度 <= 8

本题思路：

首先：采用经典的“回溯三部曲”：

       1、定义两个全局变量，一个用来存放符合条件单一结果（path），一个用来存放符合条件结果的集合（result）。

        2、回溯的主体，回溯终止条件。path保存一组数据，每次遍历到叶子节点，再插入到result中，并且回溯到上一个节点。

        3、单层搜索的过程。for循环用来横向遍历，递归的过程是纵向遍历。

根据题意我们做出一定的改动：

由于本题是以string容器的形式传递的字符串，对此，我们的path也应当转变为相应的形式。题目以及例子很明确的表现了本题实际上跟 回溯法经典问题之全排列第二小题是关系密切的。大家可参考。此题没有说明字符串内的元素是否会有相同的元素，对此，我们当做会有重复的元素，于是我们建立一个bool类型的vector容器used来作为确定每一个节点是否使用过，以此来解决重复插入问题。接着我们需要加入剪枝操作，以此来解决重复选取问题。

一句话概括此题就是：

只有当used[i]==0时才去进行后续操作。

同一树枝上可以选取，但是同一树层上不可以选取！

即{i>0&&s[i-1]==s[i]&&used[i-1]==0}才去进行后续操作。

class Solution {
private:
vector<string> result;

void trackback(string& s,string& path,vector<bool>& used)
{
    if(path.size()==s.size())
    {
        result.push_back(path);
        return;
    }

    for(int i=0;i<s.size();i++)
    {
        if(i>0&&s[i]==s[i-1]&&used[i-1]==0)
        continue;

        if (used[i] != 1)
            {
                path.push_back(s[i]);
                used[i] = 1;
                trackback(s,path,used);
                used[i] = 0;
                path.pop_back();
            }
    }
}
public:
    vector<string> permutation(string s) {
        if(s.size()==0)
            return{};
        result.clear();
        vector<bool> used;
        sort(s.begin(),s.end());//关键一步，由于不知道是否重复，所以必须要排序，以找到重复的字母
        string path="";
        used.resize(s.size());
        trackback(s,path,used);
        return result;
    }
};

特别注意！！！这里的sort操作是关键的一步！由于不知道是否重复，所以必须要排序，以找到重复的字母，让他们相邻排列。

🌺二、字母大小写全排列

题目链接：784. 字母大小写全排列

题目描述：

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。

示例 1：

输入：s = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]

示例 2:

输入: s = "3z4"
输出: ["3z4","3Z4"]

提示:

1 <= s.length <= 12
s 由小写英文字母、大写英文字母和数字组成

本题思路：

同样的，采用回溯三部曲，但是我们这次不采用for循环遍历，因为根据题意，本题仅仅只是改变“字母的大小写转化”。如下：

       1、定义两个全局变量，一个用来存放符合条件单一结果（path），一个用来存放符合条件结果的集合（result）。注意要记得用一个变量来记录遍历的位置。

        2、回溯的主体，回溯终止条件。path保存一组数据，每次遍历到叶子节点，再插入到result中，并且回溯到上一个节点。

        3、无需for循环横向遍历，仅仅纵向遍历，即递归的过程。

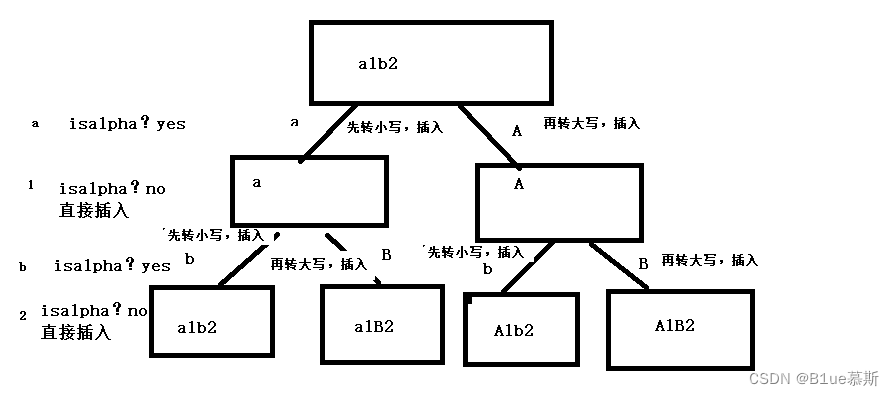
梳理一下判断的条件：判断是否为字母，如果是字母，则不管他是否为大小写，直接转化为小写插入path，进行递归，递归回来后再转化为大写插入path，递归。如果不是字母，则直接插入parh，进行下一层的递归。

一图让你了解~（以a1b2为例）

class Solution {
private:
vector<string> result;

void backtrack(string& s,string& path,int index)
{
    if(s.size()==path.size())
    {
        result.push_back(path);
        return;
    }
    if(isalpha(s[index]))
    {
        path.push_back(tolower(s[index]));
        backtrack(s,path,index+1);
        path.pop_back();
        path.push_back(toupper(s[index]));
        backtrack(s,path,index+1);
        path.pop_back();
    }else
    {
        path.push_back(s[index]);
        backtrack(s,path,index+1);
        path.pop_back();
    }
 
}
public:
    vector<string> letterCasePermutation(string s) {
        result.clear();
        string path="";
        backtrack(s,path,0);
        return result;
    }
};

感谢你耐心的看到这里ღ( ´･ᴗ･` )比心，如有哪里有错误请踢一脚作者o(╥﹏╥)o！