本文分享一篇在IJCAI2023看到的文章:Overlooked Implications of the Reconstruction Loss for VAE Disentanglement
首先回顾下VAE,其loss函数有两项,一项是重构误差,另一项是正则项:
L
r
e
c
(
x
,
x
^
)
=
E
q
ϕ
(
z
∣
x
)
[
log
p
θ
(
x
∣
z
)
]
L
r
e
g
(
x
)
=
−
D
K
L
(
q
ϕ
(
z
∣
x
)
∥
p
θ
(
z
)
)
L
V
A
E
(
x
,
x
^
)
=
L
r
e
c
(
x
,
x
^
)
+
L
r
e
g
(
x
)
\begin{aligned} \mathcal{L}_{\mathrm{rec}}(\boldsymbol{x},\hat{\boldsymbol{x}})& =\mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}|\boldsymbol{x})}\left[\log p_{\boldsymbol{\theta}}(\boldsymbol{x}|\boldsymbol{z})\right] \\ \mathcal{L}_{\mathrm{reg}}(\boldsymbol{x})& =-D_{\mathrm{KL}}\left(q_{\phi}(z|\boldsymbol{x})\parallel p_{\boldsymbol{\theta}}(\boldsymbol{z})\right) \\ \mathcal{L}_{\mathrm{VAE}}(\boldsymbol{x},\hat{\boldsymbol{x}})& =\mathcal{L}_{\mathrm{rec}}(\boldsymbol{x},\hat{\boldsymbol{x}})+\mathcal{L}_{\mathrm{reg}}(\boldsymbol{x}) \end{aligned}
Lrec(x,x^)Lreg(x)LVAE(x,x^)=Eqϕ(z∣x)[logpθ(x∣z)]=−DKL(qϕ(z∣x)∥pθ(z))=Lrec(x,x^)+Lreg(x)
训练过VAE的人或许会知道,重构项在VAE的训练的loss中占的权重是比正则项要高的,所以重构误差是VAE的主要优化目标。因此,为了降低重构误差,VAE会将那些长得像图片,放在相近的latent space中。这是因为,VAE还有一个随机采样的过程,这样,即使隐变量z随机“偏移”了一点,也能输出一个“长得像”的图片,从而降低重构误差。
那正则项的作用是什么呢,看下图

正则项越弱,则重构的部分训练将更充分,从而导致这个隐空间的overlap会更少,最极端的情况就是查表,每个图片就对应到一个特定的取值上,可以与其他图片充分的区分开来。
正则项越强,则重构的部分训练不太充分,导致隐空间的overlap会增多,也就是隐空间的区分度下降了,也就导致重构误差增大。
所以解耦这件事情,直觉上就是重构的时候,把那些较为相似(overlap)的图片聚在一起,然后又恰好成了解耦的表征。
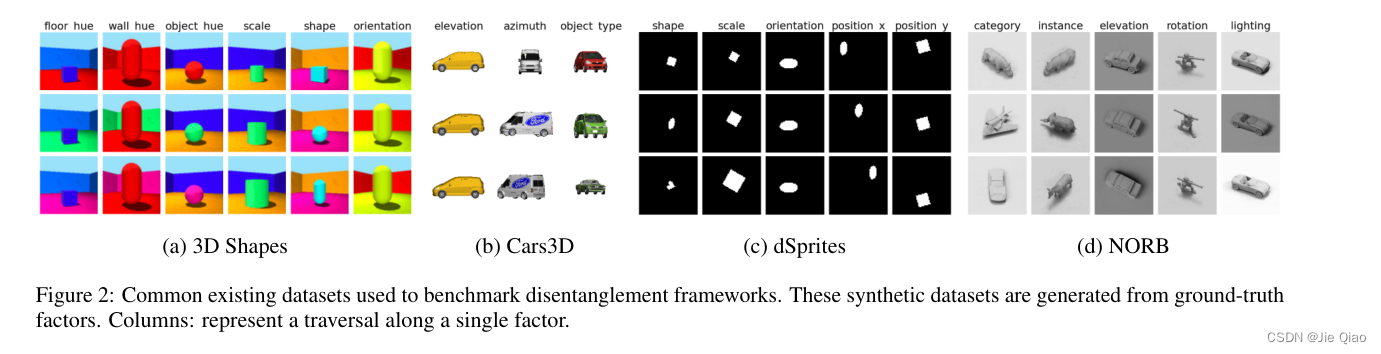
这也解释了为什么在一些解耦的数据集上,VAE能解耦的原因,因为他们的数据集是遍历所有可能出现的factor取值,然后不同取值之间有个微小切换,而其余大部分的地方是重叠的,这是这个让他学到了这个解耦的表征。
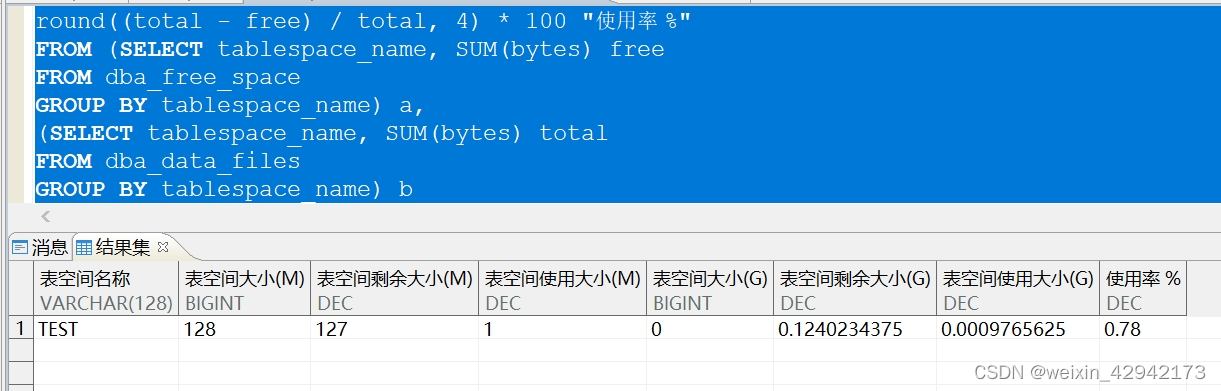
为了验证这一点,我们可以看看数据集上,图片和图片之间的距离,用
d g t ( x ( a ) , x ( b ) ) = ∥ y ( a ) − y ( b ) ∥ 1 . \operatorname{d_{gt}} (\boldsymbol{x}^{(a)} ,\boldsymbol{x}^{(b)} )=\| \boldsymbol{y}^{(a)} -\boldsymbol{y}^{(b)} \| _{1} . dgt(x(a),x(b))=∥y(a)−y(b)∥1.
这个东西可以理解为重构误差,如果我们的decoder是完美的,那么,抽样过程会引入误差, z ( b ) ∼ q ϕ ( z ∣ x ( a ) ) \displaystyle z^{( b)} \sim q_{\phi }\left( z|x^{( a)}\right) z(b)∼qϕ(z∣x(a)),从而
d p c v ( x ( a ) , x ( b ) ) = lim x ^ → x L r e c ( x ( a ) , x ^ ( b ) ) = L r e c ( x ( a ) , x ( b ) ) . \begin{aligned} \mathrm{d}_{\mathrm{pcv}} (\boldsymbol{x}^{(a)} ,\boldsymbol{x}^{(b)} ) & =\lim _{\hat{\boldsymbol{x}}\rightarrow \boldsymbol{x}}\mathcal{L}_{\mathrm{rec}} (\boldsymbol{x}^{(a)} ,\hat{\boldsymbol{x}}^{(b)} )\\ & =\mathcal{L}_{\mathrm{rec}} (x^{(a)} ,\boldsymbol{x}^{(b)} ). \end{aligned} dpcv(x(a),x(b))=x^→xlimLrec(x(a),x^(b))=Lrec(x(a),x(b)).
他固定一个factor a,然后遍历另外一个factor i,得到一组遍历的图片 Y ( a , i ) \displaystyle \mathcal{Y}^{( a,i)} Y(a,i),然后两两计算这一组图片的距离,得到下图:
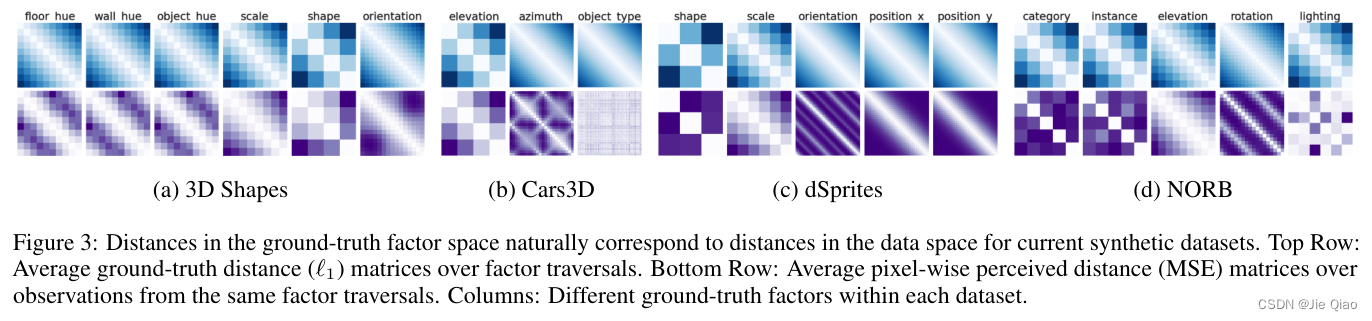
颜色越浅表示越相似,第一行是l1-norm, 第二行是MSE。可以看到他们overlap是渐进的,而且l1比mse更明显,这或许是l1比mse解耦效果好的证据,而VAE也确实能捕捉到这种overlap:
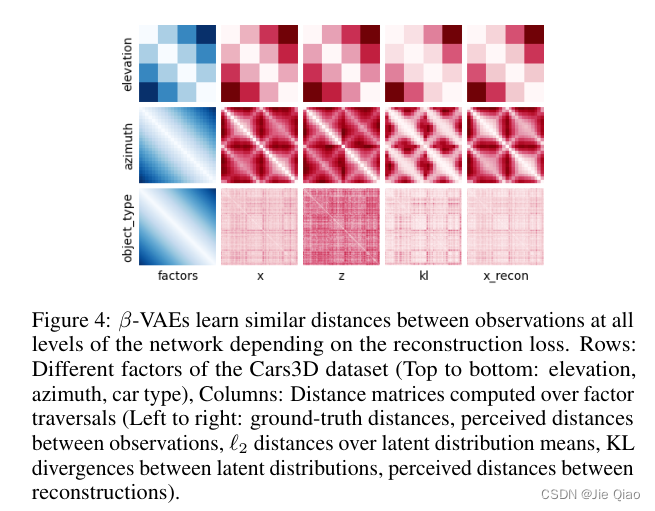
那么,如果我们能够构造一个数据集,不存在这样的渐进的overlap,是不是就意味着他学不出任何东西,因为神经网络没法通过重构误差来"聚类"了,在他眼中所有的图都是"同一类"。我们可以构造下面的数据集:
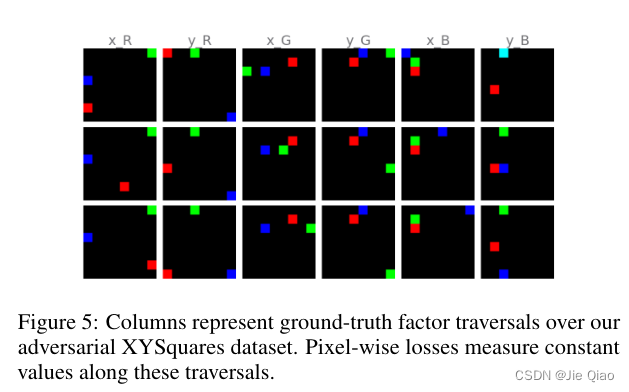
在这个数据集中,图片之间的距离都是一样的(这是因为l1-norm是计算一张图片总的loss,所以,尽管每张图片可能不一样,但只要总的差一样,则距离就相等)

上图最右边就是这个数据集的距离,而如果我们加点重叠,那么这个距离会稍微不一样:

这个对抗训练集导致的结果就是完全无法解耦:
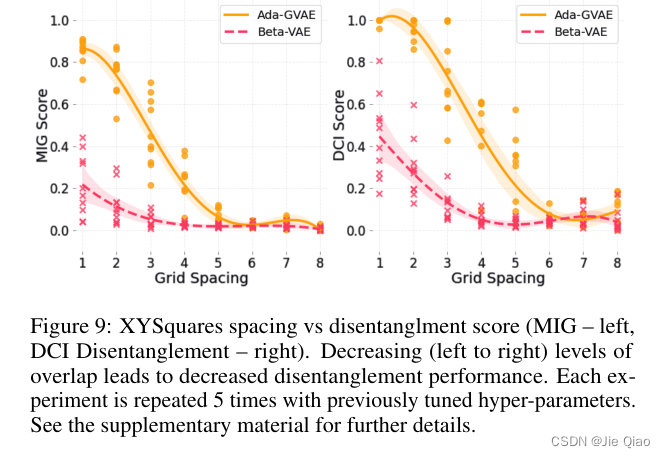
当然一个缓解的方法是换个不是pixel wise的loss,不过这个只是个缓解的方法,而且现有的半监督的方法可能也是有问题的,因为没有label的话还是会无法聚类。总的来说是篇挺有意思的工作。
参考文献
Michlo, N., Klein, R., & James, S. Overlooked Implications of the Reconstruction Loss for VAE Disentanglement. IJCAI 2023.